文章目录
- 一、似函数、非函数
- 1.1 母函数
- 1.2 母函数的简单应用
- 1.3 整数拆分
- 1.4 Ferrers 图像
- 1.5 母函数能做什么
- 1.6 递推关系
- 1.6.1 Hanoi 问题
- 1.6.2 偶数个5怎么算
- 1.7 Fibonacci 序列
- 1.7.1 Fibonacci 的奇妙性质
- 1.7.2 Fibonacci 恒等式
- 1.7.3 Fibonacci 的直接表达式
- 1.7.4 Fibonacci 优选法
- 1.8 线性常系数齐次递推关系
- 二、神奇的序列
- 2.1 Catalan 数
- 2.1.1 认识 Catalan 数
- 2.1.2 Catalan 数的直接表达式
- 2.1.3 Catalan数的其他实例
- 2.2 指数型母函数
- 2.2.1 指数型母函数的应用
- 2.3 错排
- 2.4 Stirling 数
- 2.4.1 第一类Stirling 数
- 2.4.2 第二类Stirling数
一、似函数、非函数
1.1 母函数
母函数是:
-
计数工具
-
不考虑收敛性
-
不考虑实际上的数值
-
形式幂级数(Formal power series)
对于序列C_0, C_1, C_2, … 构造一函数
G
(
x
)
=
C
0
+
C
1
x
+
C
2
x
2
+
.
.
.
G(x) = C_0 + C_1x + C_2x^2 + ...
G(x)=C0+C1x+C2x2+...
例如
(
1
+
x
)
n
(1 + x)^n
(1+x)n 称为序列 C(n, 0), C(n, 1), …, C(n, n) 的母函数,序列的长度可能是有限的,也可能是无限的。
母函数和计数法则:
例:两个色子掷出n点,有多少种可能?
一个色子的可能点数为:1、2、3、4、5、6
我们用指数来代表点数: ( x + x 2 + x 3 + x 4 + x 5 + x 6 ) (x + x^2 + x^3 + x^4 + x^5 + x^6) (x+x2+x3+x4+x5+x6)
那么两个色子投掷的表示为:
( x + x 2 + x 3 + x 4 + x 5 + x 6 ) × ( x + x 2 + x 3 + x 4 + x 5 + x 6 ) (x + x^2 + x^3 + x^4 + x^5 + x^6)\times (x + x^2 + x^3 + x^4 + x^5 + x^6) (x+x2+x3+x4+x5+x6)×(x+x2+x3+x4+x5+x6)
指数为6 即代表总点数为6,系数就是方案数,我们展开后可得 x 6 x^6 x6 的系数为5,故有 5 种方案
母函数:
- 关注每一个计数的序列
- 每一个计数序列对应的是 x k x^k xk
为什么母函数可以计算前面的色子问题?
乘法法则:
n个计数对象可以划分为i个对象和n-i个对象
加法法则:
n个计数对象所有的划分策略累加
多项式乘法运算使母函数具备了计数的能力
1.2 母函数的简单应用
计数方案
例1
有4枚砝码,分别为1、2、3、4g,问一共能称出多少种重量?
对于某一个重量,它有多少种不同的方案?
对于1g 的砝码,选或不选:1 + x
2g:1 + x^2
以此类推,所有组合的表示为母函数: G ( x ) = ( 1 + x ) ( 1 + x 2 ) ( 1 + x 3 ) ( 1 + x 4 ) = 1 + x + x 2 + 2 x 3 + 2 x 4 + 2 x 5 + 2 x 6 + 2 x 7 + x 8 + x 9 + x 10 G(x) = (1 + x)(1 + x^2)(1 + x^3)(1 + x^4)= 1+x+x^2+2x^3+2x^4+2x^5+2x^6+2x^7+x^8+x^9+x^{10} G(x)=(1+x)(1+x2)(1+x3)(1+x4)=1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10
每个幂次代表了方案,幂次的系数代表方案数
例2
若有1、2、4、8、16、32克的砝码各一枚,问能称出哪几种重量?有几种可能方案?
用母函数表示:
每一种重量都只有一种方案。
实际上,1、2、4、8、16、32 分别为 2,21,22,23,24,2^5 可以唯一组合表示出[0, 63] 内的所有整数,因为这组数字线性无关,覆盖了二进制低五位
例3:整数n拆分成1,2,……,m的和,并允许重复,求其母函数。
把式子展开即可得到具体方案
如若其中m至少出现一次,其母函数如何?
上式的组合意义:即整数n拆分成1到m的和的拆分数减去拆分成1到m-1的和的拆分数,即为至少出现一个m的拆分数。
1.3 整数拆分
将一个正整数拆分成若干个正整数之和。
如果考虑各部分之间的顺序,那么称为有序拆分(Composition)
比如 3 = 1 + 2 和 3 = 2 + 1 两个是不等价的有序拆分。
各部分之间不考虑顺序,那么称为无序拆分(Partition)
数字n拆分成r个自然数之和,有多少种不同的拆分方案?

根据隔板法可得:C(n - 1, r - 1)
那么无序拆分呢?
无序拆分方案数 和 线性方程解的个数等价吗?
x1 + x2 + … + xn = b 非负整数解的个数为 C(n + b - 1, b)
显然不等价,3 + 0 + 0 和 0 + 3 + 0 是两组解,却是同一组无序拆分。
有序拆分相当于把 n 个无区别的球放到 r 个有标志的盒子,盒子不允许空着。
无序拆分把一个整数分解成若干整数的和,相当于把 n 个无区别的球放到 r 个无标志的盒子,盒子允许空着,有多少种方法,就意味着整数拆分数有多少。
无序拆分数:将一个正整数 n 拆分成若干正整数的和,数字之间顺序无关并允许重复,其不同的拆分数即 p(n)。
比如,p(3) = 3
非常有趣的是,欧拉并不知道母函数的概念,但当诺地向欧拉写信询问整数拆分数问题时,欧拉直接给出整数拆分数实际上等于:
G ( x ) = ( 1 + x + x 2 + . . . ) ( 1 + x 2 + x 4 + . . . ) . . . ( 1 + x m + x 2 m + . . . ) . . . G(x) = (1+x+x^2+...)(1+x^2+x^4+...)...(1+x^m+x^{2m}+...)... G(x)=(1+x+x2+...)(1+x2+x4+...)...(1+xm+x2m+...)... 中 x n x^n xn 的系数。
这并不难理解,不再解释。
但是多项式乘法复杂度还是比较高的(在古法计算的年代,没有计算机和各种优化算法),而注意力惊人的拉马努金提出神秘猜想,把整数拆分数计算到了p(200)。
1.4 Ferrers 图像

Ferrers 用 n 个格子的摆放方案来表示整数的无序分拆数。
Ferrers 图像要求非递增性:上一层的格子不能比下一层的格子少。
第 i 行的格子数目代表第 i 个数是多少。
Ferrers 图像具有如下性质:
- 每一层至少有一个格子。
- 第一行与第一列互换,第二行于第二列互换,…,绕虚线轴旋转所得的图仍然是 Ferrers 图像。两个 Ferrers 图像称为一对共轭的Ferrers 图像。
结论:整数 n 拆分成最大数为 k 的拆分数,和数 n 拆分成 k 个数的和的拆分数相等。
- 很好理解,任何一个Ferrers 图像经过翻转后仍然是一个Ferrers 图像,我们不难建立起两个集合的1-1映射。
- 最大数是k和变成k个数之和,它们的 Ferrers 图像是一一对应的。
结论:整数 n 拆分成最多不超过 m 个数的和的拆分数,和 n 拆分成最大不超过 m 的拆分数相等。
- 同样可以利用Ferrers 图像证明
结论:整数拆分成互不相同的若干奇数的和的拆分数,和拆分成自共轭的 Ferrers 图像的拆分数相等。
- 自共轭Ferrers图像:翻转后和翻转前相同
如何建立起自共轭 Ferrers 图像和 奇数拆分 之间的1-1 映射关系呢?
对于一个若干奇数的拆分: ( 2 n 1 + 1 ) + ( 2 n 2 + 1 ) + . . . + ( 2 n k + 1 ) (2n_1 + 1) + (2n_2 + 1) + ... + (2n_k + 1) (2n1+1)+(2n2+1)+...+(2nk+1)
而对于一个自共轭图像,第一行和第一列加起来一共有: 2 n 1 + 1 2n_1 + 1 2n1+1 个格子
第二行和第二列加起来一共有: 2 n 2 + 1 2n_2 + 1 2n2+1 个格子
……
所以对于一个自共轭Ferrers 图像总能和一个 奇数拆分对应,一个奇数拆分总能和一个自共轭Ferrers 图像对应。
例如:

1.5 母函数能做什么

我们通过二项式定理得到一系列的 x^k 前面有系数的展开式,从而得到 某个母函数。
我们可以通过部分分式分解,将一个复杂的母函数对应到一个数字序列。
比如
2
−
3
x
(
1
−
x
)
(
1
−
2
x
)
=
1
1
−
x
+
1
1
−
2
x
=
∑
k
=
0
∞
x
k
+
∑
k
=
0
∞
2
k
x
k
=
∑
k
=
0
∞
(
1
+
2
k
)
x
k
\begin{align} \frac{2-3x}{(1-x)(1-2x)} &= \frac{1}{1-x} + \frac{1}{1-2x} \\ &= \sum_{k=0}^{\infin}x^k + \sum_{k=0}^{\infin}2^kx^k \\ &= \sum_{k=0}^{\infin}(1+2^k)x^k \\ \end{align}
(1−x)(1−2x)2−3x=1−x1+1−2x1=k=0∑∞xk+k=0∑∞2kxk=k=0∑∞(1+2k)xk
2
−
3
x
(
1
−
x
)
(
1
−
2
x
)
是序列
f
(
k
)
=
2
k
+
1
的母函数
\frac{2-3x}{(1-x)(1-2x)}是序列f(k) = 2^k + 1的母函数
(1−x)(1−2x)2−3x是序列f(k)=2k+1的母函数
我们也知道,2^k + 1 也可以写成一个递推式子:h(k) = 2h(k - 1) + 1
递推关系在计算机界是一类很重要的问题,我们是否能通过母函数来求解递推关系呢?
1.6 递推关系
**递推关系(Recurrence Relation)**即差分方程。
是一种递推地定义一个序列的方程式:序列的每一项目定义为前若干项的函数.
1.6.1 Hanoi 问题
- 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
- 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
- 在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
我们设移动 n个盘子的时间复杂度为 h(n)。
学习递归的时候都讲过汉诺塔的策略:
- 将A的上面n - 1 个 盘子借助C移动到B
- 将A的最后一个盘子移动到C
- 将B 剩的n - 1 个 盘子借助A 移动到C
根据策略可以得到递推方程:h(n) = 2h(n - 1) + 1
显然有初值 h(1) = 1
我们写出 h(n) 的母函数:G(x) = h(1)x + h(2)x^x + h(3)x^3 …
然后可以利用错位相减法来求解:
H
(
x
)
=
h
(
1
)
x
+
h
(
2
)
x
2
+
h
(
3
)
x
3
+
.
.
.
①
−
2
x
H
(
x
)
=
−
2
h
(
1
)
x
−
2
h
(
2
)
x
3
+
.
.
.
②
(
1
−
2
x
)
H
(
x
)
=
h
(
1
)
x
+
[
h
(
2
)
−
h
(
1
)
]
x
2
+
[
h
(
3
)
−
2
h
(
2
)
]
x
3
+
.
.
.
①
+
②
(
1
−
2
x
)
H
(
x
)
=
x
+
x
2
+
x
3
+
.
.
.
=
x
1
−
x
H
(
x
)
=
x
(
1
−
2
x
)
(
1
−
x
)
\begin{align} & H(x) = h(1)x + h(2)x^2 + h(3)x^3 + ...① \\ & -2xH(x) = -2h(1)x - 2h(2)x^3 + ...②\\ & (1-2x)H(x) = h(1)x + [h(2) - h(1)]x^2 + [h(3) - 2h(2)]x^3 + ... ① + ②\\ & (1-2x)H(x) = x + x^2 + x^3+... = \frac{x}{1-x} \\ & H(x) = \frac{x}{(1-2x)(1-x)} \end{align}
H(x)=h(1)x+h(2)x2+h(3)x3+...①−2xH(x)=−2h(1)x−2h(2)x3+...②(1−2x)H(x)=h(1)x+[h(2)−h(1)]x2+[h(3)−2h(2)]x3+...①+②(1−2x)H(x)=x+x2+x3+...=1−xxH(x)=(1−2x)(1−x)x
也可以根据递推关系求解:
H
(
x
)
=
h
(
1
)
x
+
h
(
2
)
x
2
+
h
(
3
)
x
3
+
.
.
.
H
(
x
)
−
h
(
1
)
x
=
(
2
h
(
1
)
+
1
)
x
2
+
(
2
h
(
2
)
+
1
)
x
3
+
.
.
.
H
(
x
)
−
h
(
1
)
x
=
2
x
H
(
x
)
+
x
2
1
−
x
H
(
x
)
=
x
(
1
−
x
)
(
1
−
2
x
)
\begin{align} & H(x) = h(1)x + h(2)x^2 + h(3)x^3 + ...\\ & H(x) - h(1)x = (2h(1) + 1)x^2 + (2h(2) + 1)x^3 + ... \\ & H(x) - h(1)x = 2xH(x) + \frac{x^2}{1-x} \\ & H(x) = \frac{x}{(1-x)(1-2x)} \end{align}
H(x)=h(1)x+h(2)x2+h(3)x3+...H(x)−h(1)x=(2h(1)+1)x2+(2h(2)+1)x3+...H(x)−h(1)x=2xH(x)+1−xx2H(x)=(1−x)(1−2x)x
现在已知
H
(
x
)
=
∑
k
=
1
∞
h
(
k
)
x
2
=
x
(
1
−
x
)
(
1
−
2
x
)
H(x) = \sum_{k=1}^{\infin} h(k)x^2 = \frac{x}{(1-x)(1-2x)}
H(x)=∑k=1∞h(k)x2=(1−x)(1−2x)x,如何从母函数得到序列?
上式一定可以化简为: H ( x ) = A 1 − x + B 1 − 2 x H(x) = \frac{A}{1-x} + \frac{B}{1-2x} H(x)=1−xA+1−2xB
我们待定系数法不难算出:
H
(
x
)
=
1
1
−
2
x
−
1
1
−
x
=
(
1
+
2
x
+
2
2
x
2
+
.
.
.
)
−
(
1
+
x
+
x
2
+
.
.
.
)
=
∑
k
=
1
∞
(
2
k
−
1
)
x
k
\begin{align} H(x) &= \frac{1}{1-2x} - \frac{1}{1-x}\\ &= (1+2x+2^2x^2+...) - (1+x+x^2+...) \\ &= \sum_{k=1}^{\infin}(2^k-1)x^k \end{align}
H(x)=1−2x1−1−x1=(1+2x+22x2+...)−(1+x+x2+...)=k=1∑∞(2k−1)xk
1.6.2 偶数个5怎么算
求 n 位十进制数中出现偶数个5的数的个数。
F1:令 a n a_n an为n位十进制数中出现偶数个5的数的个数, b n b_n bn为n位十进制数中出现奇数个5的数的个数。
不难得出递推:
a
n
=
9
a
n
−
1
+
b
n
−
1
b
n
=
9
b
n
−
1
+
a
n
−
1
a
1
=
8
,
b
1
=
1
a_n = 9a_{n-1} + b_{n - 1} \\ b_n = 9b_{n-1} + a_{n - 1} \\ a_1 = 8, b_1 = 1
an=9an−1+bn−1bn=9bn−1+an−1a1=8,b1=1
联立:
A
(
x
)
=
a
1
+
a
2
x
+
a
3
x
3
+
.
.
.
−
9
x
A
(
x
)
=
−
9
a
1
x
−
9
a
2
x
2
−
.
.
.
−
x
B
(
x
)
=
−
b
1
x
−
b
2
x
2
−
.
.
.
(
1
−
9
x
)
A
(
x
)
−
x
B
(
x
)
=
a
1
=
8
同理可得
:
(
1
−
9
x
)
B
(
x
)
−
x
A
(
x
)
=
1
\begin{align} A(x) &= a_1 + a_2x + a_3x^3 + ... \\ -9xA(x) &= -9a_1x - 9a_2x^2 - ... \\ -xB(x) &= -b_1x - b_2x^2 - ... \\ (1-9x)A(x) - xB(x) &= a_1 = 8 \\ 同理可得:(1-9x)B(x) - xA(x) &= 1 \end{align}
A(x)−9xA(x)−xB(x)(1−9x)A(x)−xB(x)同理可得:(1−9x)B(x)−xA(x)=a1+a2x+a3x3+...=−9a1x−9a2x2−...=−b1x−b2x2−...=a1=8=1
A(x) 和 B(x) 的求解方式可以通过克莱姆法则来求:
得到 a k = 7 2 8 k − 1 + 9 2 1 0 k − 1 a_k = \frac{7}{2}8^{k-1} + \frac{9}{2}10^{k - 1} ak=278k−1+2910k−1
F2:
n 位的全体十进制数目有 9 ∗ 1 0 n − 1 9 * 10^{n - 1} 9∗10n−1 个(最高位不为0),设所求数为 a n a_n an, A ( x ) = a 1 x + a 2 x + . . . A(x) = a_1x + a_2x + ... A(x)=a1x+a2x+...
按最后一位是否为5分类:
尾数不为5: 9 ∗ a n − 1 9 * a_{n - 1} 9∗an−1
尾数为5,前n - 1有奇数个5: b n − 1 = 9 ∗ 1 0 n − 2 − a n − 1 b_{n - 1} = 9 *10^{n - 2} - a_{n-1} bn−1=9∗10n−2−an−1
故 a n = 9 a n − 1 + 9 ∗ 1 0 n − 2 − a n − 1 = 8 a n − 1 + 9 ∗ 1 0 n − 2 , a 1 = 8 a_n = 9a_{n-1} + 9*10^{n-2} - a_{n-1} = 8a_{n-1} + 9*10^{n-2}, a_1 = 8 an=9an−1+9∗10n−2−an−1=8an−1+9∗10n−2,a1=8
A ( x ) − a ( x ) = 8 x A ( x ) + 9 x 2 ( 1 + 10 x + 1 0 2 x 2 . . . . . . ) A(x) - a(x) = 8xA(x) + 9x^2(1 + 10x + 10^2x^2......) A(x)−a(x)=8xA(x)+9x2(1+10x+102x2......)
A ( x ) = x ( 8 − 71 x ) ( 1 − 8 x ) ( 1 − 10 x ) = 1 2 ( 7 x 1 − 8 x + 9 x 1 − 10 x ) = 1 2 ∑ k = 1 ∞ ( 7 ∗ 8 k − 1 + 9 ∗ 1 0 k − 1 ) x k A(x) = \frac{x(8-71x)}{(1-8x)(1-10x)} = \frac{1}{2}(\frac{7x}{1-8x}+\frac{9x}{1-10x}) = \frac{1}{2}\sum_{k=1}^{\infin}{(7*8^{k-1} + 9*10^{k-1})x^k} A(x)=(1−8x)(1−10x)x(8−71x)=21(1−8x7x+1−10x9x)=21∑k=1∞(7∗8k−1+9∗10k−1)xk
得到 a k = 7 2 8 k − 1 + 9 2 1 0 k − 1 a_k = \frac{7}{2}8^{k-1} + \frac{9}{2}10^{k - 1} ak=278k−1+2910k−1
1.7 Fibonacci 序列
Fibonacci 递推公式:F(n) = F(n - 1) + F(n - 2),F(1) = F(2) = 1
1.7.1 Fibonacci 的奇妙性质
Fibonacci 与 杨辉三角

杨辉三角每一条斜线的和构成了Fibonacci 数
Fibonacci 与 分支开叶

自然界中,树的枝条数目满足Fibonacci数
Fibonacci 的周期性
- 最后一位数字,每60个数一循环
- 最后两位数字,每300个数一循环;
- 最后三位数字,每1500个数一循环;
- 最后四位数字,每15000个数一循环;
- 最后五位数字,每150000个数一循环;
- ……
Fibonacci 的整除性
- 每第三个数可被2整除
- 每第四个数可被3整除
- 每第五个数可被5整除
- 每第六个数可被8整除
- ……
- 这些除数市身也构成裴波那契数列。
Fibonacci Prime
- 除了n=4之外,所有的Fibonacci primes的序号都是素数。
1.7.2 Fibonacci 恒等式
1、 F 1 2 + F 2 2 + . . . + F n 2 = F n F n + 1 F_1^2 + F_2^2 + ... + F_n^2 = F_nF_{n+1} F12+F22+...+Fn2=FnFn+1
几何证明:

Fibonacci 的平方和可以看作若干个长为Fibonacci数的正方形的拼接,最后会得到一个长为F(n + 1),宽为F(n)的长方形。
数学证明:
F
1
2
=
F
2
F
1
F
2
2
=
F
2
(
F
3
−
F
1
)
=
F
2
F
3
−
F
2
F
1
F
3
2
=
F
3
(
F
4
−
F
2
)
=
F
3
F
4
−
F
2
F
3
.
.
.
.
.
.
F
n
2
=
F
n
(
F
n
+
1
−
F
n
−
1
)
=
F
n
F
n
+
1
−
F
n
−
1
F
n
累加得:
F
1
2
+
F
2
2
+
.
.
.
+
F
n
2
=
F
n
F
n
+
1
\begin{align} & F_1^2 = F_2F_1 \\ & F_2^2 = F2(F_3 - F_1) = F_2F_3 - F_2F_1 \\ & F_3^2 = F_3(F_4 - F_2) = F_3F_4 - F_2F_3 \\ & ...... \\ & F_n^2 = F_n(F_{n+1} - F_{n-1}) = F_nF_{n + 1} - F_{n - 1}F_n \\ & 累加得:F_1^2 + F_2^2 + ... + F_n^2 = F_nF_{n+1} \end{align}
F12=F2F1F22=F2(F3−F1)=F2F3−F2F1F32=F3(F4−F2)=F3F4−F2F3......Fn2=Fn(Fn+1−Fn−1)=FnFn+1−Fn−1Fn累加得:F12+F22+...+Fn2=FnFn+1
2、
F
1
+
F
2
+
.
.
.
+
F
n
=
F
n
+
2
−
1
F_1 + F_2 + ... + F_n = F_{n + 2} - 1
F1+F2+...+Fn=Fn+2−1
证明:
F
1
=
F
3
−
F
2
F
2
=
F
4
−
F
3
.
.
.
F
n
−
1
=
F
n
+
1
−
F
n
F
n
=
F
n
+
2
−
F
n
+
1
累加得:
F
1
+
F
2
+
.
.
.
+
F
n
=
F
n
+
2
−
1
\begin{align} & F_1 = F_3 - F_2 \\ & F_2 = F_4 - F_3 \\ & ... \\ & F_{n-1} = F_{n + 1} - F_n \\ & F_n = F_{n + 2} - F_{n + 1} \\ & 累加得:F_1 + F_2 + ... + F_n = F_{n + 2} - 1 \end{align}
F1=F3−F2F2=F4−F3...Fn−1=Fn+1−FnFn=Fn+2−Fn+1累加得:F1+F2+...+Fn=Fn+2−1
3、
F
1
+
F
3
+
F
5
+
.
.
.
+
F
2
n
−
1
=
F
2
n
F_1 + F_3 + F_5 + ... + F_{2n - 1} = F_{2n}
F1+F3+F5+...+F2n−1=F2n
证明:
F
1
=
F
2
F
3
=
F
4
−
F
2
F
5
=
F
6
−
F
4
.
.
.
F
2
n
−
1
=
F
2
n
−
F
2
n
−
2
累加得:
F
1
+
F
3
+
F
5
+
.
.
.
+
F
2
n
−
1
=
F
2
n
\begin{align} & F_1 = F_2 \\ & F_3 = F_4 - F_2 \\ & F_5 = F_6 - F_4 \\ & ... \\ & F_{2n - 1} = F_{2n} - F_{2n - 2} \\ & 累加得:F_1 + F_3 + F_5 + ... + F_{2n - 1} = F_{2n} \end{align}
F1=F2F3=F4−F2F5=F6−F4...F2n−1=F2n−F2n−2累加得:F1+F3+F5+...+F2n−1=F2n
1.7.3 Fibonacci 的直接表达式
G ( x ) = F 1 x + F 2 x 2 + . . . G ( x ) − x − x 2 = x ( G ( x ) − x ) + x 2 G ( x ) G ( x ) = x 1 − x − x 2 = x ( 1 − 1 − 5 2 x ) ( 1 + 1 + 5 2 x ) = A 1 − 1 + 5 2 x + B 1 − 1 − 5 2 x 求得 A = 1 5 , B = − 1 5 G ( x ) = 1 5 [ 1 1 − 1 + 5 2 x − 1 1 − 1 − 5 2 x ] = 1 5 [ ( α − β ) x + ( α 2 − β 2 ) x 2 + . . . ] \begin{align} & G(x) = F_1x + F_2x^2 + ... \\ & G(x) - x - x^2 = x(G(x) - x) + x^2G(x) \\ & G(x) = \frac{x}{1-x-x^2} \\ &= \frac{x}{(1-\frac{1-\sqrt{5}}{2}x)(1+\frac{1+\sqrt{5}}{2}x)} \\ &=\frac{A}{1-\frac{1+\sqrt{5}}{2}x} + \frac{B}{1 - \frac{1-\sqrt{5}}{2}x} \\ & 求得 A = \frac{1}{\sqrt 5}, B = -\frac{1}{\sqrt5} \\ & G(x) = \frac{1}{\sqrt 5}[\frac{1}{1 - \frac{1+\sqrt 5}{2}x} - \frac{1}{1 - \frac{1-\sqrt 5}{2}x}] \\ &= \frac{1}{\sqrt 5}[(\alpha - \beta)x + (\alpha ^2 - \beta ^2)x^2 + ...] \end{align} G(x)=F1x+F2x2+...G(x)−x−x2=x(G(x)−x)+x2G(x)G(x)=1−x−x2x=(1−21−5x)(1+21+5x)x=1−21+5xA+1−21−5xB求得A=51,B=−51G(x)=51[1−21+5x1−1−21−5x1]=51[(α−β)x+(α2−β2)x2+...]
注:α和β只是省略写法。
最终求得: F n = 1 5 ( ( 1 + 5 2 ) 2 − ( 1 − 5 2 ) 2 ) F_n = \frac{1}{\sqrt 5}((\frac{1+\sqrt 5}{2})^2 - (\frac{1-\sqrt 5}{2})^2) Fn=51((21+5)2−(21−5)2)
我们发现 F n + 1 F n ≈ 1 + 5 2 ≈ 1.618 \frac{F_{n + 1}}{F_n} \approx \frac{1+\sqrt 5}{2} \approx 1.618 FnFn+1≈21+5≈1.618,正好是黄金分割。
1.7.4 Fibonacci 优选法
其实就是Fibonacci 查找。
对于一个单峰函数f(x),设 f(x) 在 x = ε 点取得极大值。要求用若干次试验找到ε点准确到一定的程度。最简单的方法,把 (a, b) 三等分。

在做算法题的时候一般会采用三分查找(二分也可以,不过要处理好细节)。
三分查找每次选取区间的 1 / 3 和 2 / 3 点作为测试点
有人想到可以利用黄金比例来选取测试点,即 每次选取 0.382 和 0.618 测试点。
而Fibonacci 优选法采用Fibonacci 数列来选取测试点。
因为 F(n + 1) / F(n) -> 0.618
假设 当前区间为[0, F(n)](如果实际不够的话,我们可以将区间扩展为某个Fibonacci数)

选取 F(n - 2) 和 F(n - 1) 作为测试点
- 如果 F(n - 2) 处更好,我们舍去[F(n - 1), F(n)]
- 否则,舍去[0, F(n - 2)]
- 如此,不断逼近,可以得出结果。
1.8 线性常系数齐次递推关系
这一部分类似于微分方程。
定义
a
n
+
c
1
a
n
−
1
+
c
2
a
n
−
2
+
.
.
.
+
a
k
a
n
−
k
=
0
a
0
=
d
0
,
a
1
=
d
1
,
.
.
.
,
c
k
−
1
=
d
k
−
1
\begin{align} & a_n + c_1a_{n-1} + c_2a_{n-2} + ... + a_ka_{n-k} = 0 \\ & a_0 = d_0, a_1 = d_1, ..., c_{k-1} = d_{k-1} \end{align}
an+c1an−1+c2an−2+...+akan−k=0a0=d0,a1=d1,...,ck−1=dk−1
若
c
1
,
c
2
,
.
.
.
,
c
k
,
d
0
,
d
1
,
.
.
.
,
d
k
−
1
c_1, c_2, ..., c_k, d_0, d_1, ..., d_{k-1}
c1,c2,...,ck,d0,d1,...,dk−1 都是常数,那么上式被称为 k 阶线性常系数齐次递推关系。
例如,FIbonacci 数{
F
n
F_n
Fn} 满足:
F
n
−
F
n
−
1
−
F
n
−
2
=
0
,
F
1
=
F
2
=
1
F_n - F_{n-1} - F_{n-2} = 0, F_1 = F_2 = 1
Fn−Fn−1−Fn−2=0,F1=F2=1
- 线性累加和
- 右端项为0
- 系数是常数
对于线性常系数齐次递推关系,我们可以通过母函数方法,高效求解。
以线性常系数齐次递推关系定义式为例:
设 G(x) 为 { a n a_n an} 的母函数 G ( x ) = a 0 + a 1 x + . . . + a n x n + . . . G(x) = a_0 + a_1x + ... + a_nx^n + ... G(x)=a0+a1x+...+anxn+...
根据定义式得:
x
k
:
a
k
+
c
1
a
k
−
1
+
c
2
a
k
−
2
+
.
.
.
+
c
k
−
1
a
1
+
c
k
a
0
=
0
x
k
+
1
:
a
k
+
1
+
c
1
a
k
+
c
2
a
k
−
1
+
.
.
.
+
c
k
−
1
a
2
+
c
k
a
1
=
0
x
k
+
2
:
a
k
+
2
+
c
1
a
k
+
1
+
c
2
a
k
+
.
.
.
+
c
k
−
1
a
3
+
c
k
a
2
=
0
.
.
.
\begin{align} & x^k: a_k + c_1a_{k-1} + c_2a_{k-2} + ... + c_{k-1}a_1 + c_ka_0 = 0 \\ & x^{k+1}: a_{k+1} + c_1a_{k} + c_2a_{k-1} + ... + c_{k-1}a_2 + c_ka_1 = 0 \\ & x^{k+2}: a_{k+2} + c_1a_{k+1} + c_2a_{k} + ... + c_{k-1}a_3 + c_ka_2 = 0 \\ & ... \end{align}
xk:ak+c1ak−1+c2ak−2+...+ck−1a1+cka0=0xk+1:ak+1+c1ak+c2ak−1+...+ck−1a2+cka1=0xk+2:ak+2+c1ak+1+c2ak+...+ck−1a3+cka2=0...
两边分别相加得到:
G
(
x
)
−
∑
i
=
0
k
−
1
a
i
x
i
+
c
1
x
(
G
(
x
)
−
∑
i
=
0
k
−
2
a
i
x
i
)
+
.
.
.
+
c
k
x
k
G
(
x
)
=
0
G(x) - \sum_{i=0}^{k-1}a_ix^i + c_1x(G(x) - \sum_{i=0}^{k-2}a_ix^i) + ... + c_kx^kG(x) = 0
G(x)−i=0∑k−1aixi+c1x(G(x)−i=0∑k−2aixi)+...+ckxkG(x)=0
化简:
(
1
+
c
1
x
+
c
2
x
2
+
.
.
.
+
c
k
x
k
)
G
(
x
)
=
∑
j
=
0
k
−
1
c
j
x
j
∑
i
=
0
k
−
1
−
j
a
i
x
i
(1 + c_1x + c_2x^2 + ... + c_kx^k)G(x) = \sum_{j=0}^{k-1}c_jx^j\sum_{i=0}^{k-1-j}a_ix^i
(1+c1x+c2x2+...+ckxk)G(x)=j=0∑k−1cjxji=0∑k−1−jaixi
其中 定义
c
0
=
1
,令
P
(
x
)
=
∑
j
=
0
k
−
1
c
j
x
j
∑
i
=
0
k
−
1
−
j
a
i
x
i
,
P
(
x
)
的次方不超过
k
−
1
,
则
c_0 = 1,令 P(x) = \sum_{j=0}^{k-1}c_jx^j\sum_{i=0}^{k-1-j}a_ix^i,P(x) 的次方不超过k - 1, 则
c0=1,令P(x)=∑j=0k−1cjxj∑i=0k−1−jaixi,P(x)的次方不超过k−1,则
G
(
x
)
=
P
(
x
)
1
+
c
1
x
+
c
2
x
2
+
.
.
.
+
c
k
x
k
=
P
(
x
)
R
(
x
)
G(x) = \frac{P(x)}{1+c_1x+c_2x^2+...+c_kx^k} = \frac{P(x)}{R(x)}
G(x)=1+c1x+c2x2+...+ckxkP(x)=R(x)P(x)
我们定义特征多项式:
C
(
x
)
=
x
k
+
c
1
x
k
−
1
+
.
.
.
+
c
k
−
1
x
+
c
k
C(x) = x^k + c_1x^{k-1} + ... + c_{k-1}x + c_k
C(x)=xk+c1xk−1+...+ck−1x+ck,C(x) = 0 有 k 个 根
C ( x ) = ( x − α 1 ) k 1 ( x − α 2 ) k 2 . . . ( x − α t ) k t , k 1 + k 2 + . . . + k t = k C(x) = (x - \alpha_1)^{k_1}(x-\alpha_2)^{k_2}...(x-\alpha_t)^{k_t}, k_1+k_2+...+k_t = k C(x)=(x−α1)k1(x−α2)k2...(x−αt)kt,k1+k2+...+kt=k
则 G ( x ) = P ( x ) x k C ( 1 x ) = P ( x ) ( 1 − α 1 x ) k 1 ( 1 − α 2 x ) k 2 . . . ( 1 − α t x ) k t G(x) = \frac{P(x)}{x^kC(\frac{1}{x})} = \frac{P(x)}{(1-\alpha_1x)^{k_1}(1-\alpha_2x)^{k_2}...(1-\alpha_tx)^{k_t}} G(x)=xkC(x1)P(x)=(1−α1x)k1(1−α2x)k2...(1−αtx)ktP(x)
也就是说,线性常系数齐次递推关系都可以化成如上形式,那么我们只需求特征多项式,解特征方程即可。
例1
Fibonacci 数列递推关系
F n = F n − 1 + F n − 2 , F 1 = F 2 = 0 F_n = F_{n - 1} + F_{n - 2}, F_1 = F_2 = 0 Fn=Fn−1+Fn−2,F1=F2=0
特征方程:x^2 - x - 1 = 0
两个根: α = 1 + 5 2 , β = 1 − 5 2 \alpha = \frac{1+\sqrt 5}{2},\beta = \frac{1-\sqrt 5}{2} α=21+5,β=21−5
待定系数 G ( x ) = A 1 − α x + B 1 − β x G(x) = \frac{A}{1 - \alpha x} + \frac{B}{1 - \beta x} G(x)=1−αxA+1−βxB
由 F 0 = A + B = 0 , F 1 = A α + B β = 1 F_0 = A + B = 0, F_1 = A\alpha + B\beta = 1 F0=A+B=0,F1=Aα+Bβ=1得
A = 1 5 , B = − 1 5 A = \frac{1}{\sqrt{5}}, B = -\frac{1}{\sqrt 5} A=51,B=−51
F n = ( α n − β n ) / 5 F_n = (\alpha ^n - \beta ^n) / \sqrt 5 Fn=(αn−βn)/5
例2(多重根的情况)
a n − 4 a n − 1 + 4 a n − 2 = 0 , a 0 = 1 , a 1 = 4 a_n - 4a_{n-1} + 4a_{n-2} = 0, a_0 =1, a_1 = 4 an−4an−1+4an−2=0,a0=1,a1=4
特征方程: x 2 − 4 x + 4 = 0 x^2 - 4x + 4 = 0 x2−4x+4=0
α = β = 2 \alpha = \beta = 2 α=β=2
G(x) = a x + b ( 1 − 2 x ) 2 \frac{ax+b}{(1-2x)^2} (1−2x)2ax+b
a 0 = 1 , a 1 = 4 = > a = 1 , b = 1 a_0 = 1, a_1 = 4 => a = 1,b = 1 a0=1,a1=4=>a=1,b=1
所以 G ( x ) = A ( 1 − 2 x ) 2 = ∑ k = 0 ∞ C ( k + 1 , k ) 2 k x k = ∑ k = 0 ∞ ( k + 1 ) 2 k x k G(x) = \frac{A}{(1-2x)^2} = \sum_{k=0}^{\infin}C(k + 1, k)2^kx^k = \sum_{k=0}^{\infin}(k + 1)2^kx^k G(x)=(1−2x)2A=∑k=0∞C(k+1,k)2kxk=∑k=0∞(k+1)2kxk
a n = ( n + 1 ) 2 n a_n = (n + 1)2^n an=(n+1)2n
例3(复根情况)
a n − a n − 1 + a n − 2 = 0 , a 1 = 1 , a 2 = 0 , a 0 = 1 a_n - a_{n - 1} + a_{n - 2} = 0, a_1 = 1, a_2 = 0, a_0 = 1 an−an−1+an−2=0,a1=1,a2=0,a0=1
特征方程: x 2 − x + 1 = 0 x^2 - x + 1 = 0 x2−x+1=0,根 α = 1 2 ± − 3 2 \alpha = \frac{1}{2} \pm \frac{\sqrt{-3}}{2} α=21±2−3
G ( x ) = A 1 − 1 + − 3 2 x + B 1 − 1 − − 3 2 x G(x) = \frac{A}{1 - \frac{1 + \sqrt{-3}}{2}x} + \frac{B}{1 - \frac{1-\sqrt{-3}}{2}x} G(x)=1−21+−3xA+1−21−−3xB
由 a 0 = A + B = 1 , a 1 = A ( 1 + 3 i 2 ) + B ( 1 − 3 i 2 ) = 1 a_0 = A + B = 1,a_1 = A(\frac{1+\sqrt3i}{2}) + B(\frac{1-\sqrt3i}{2}) = 1 a0=A+B=1,a1=A(21+3i)+B(21−3i)=1
得 A = 1 2 [ 1 − 1 3 i ] A = \frac{1}{2}[1 - \frac{1}{\sqrt3}i] A=21[1−31i]
B = 1 2 [ 1 + 1 3 i ] B = \frac{1}{2}[1 + \frac{1}{\sqrt3}i] B=21[1+31i]
写成欧拉公式形式:
a n = c o s n π 3 + 1 3 s i n n π 3 a_n = cos\frac{n\pi}{3} + \frac{1}{\sqrt 3}sin \frac{n\pi}{3} an=cos3nπ+31sin3nπ
例4
例:平面上有一点P,它是n个域D1,D…,D"的共同交界点,取k种颜色对这n个域进行着色,要求相邻两个域进行着色,要求相邻两个域着的颜色不同。试求着色的方案数。
不难建立递推关系:
设 dp(n) 为 n 个 域 用k种颜色 着色方案数
那么 D1 和 Dn 可以分为两种情况:
D1 和 Dn 颜色相同:dp(n - 2) * k
D1 和 Dn 颜色不同:dp(n - 1) * (k - 2)
那么 dp(n) = dp(n - 2) * k + dp(n - 1) * (k - 2)
初始值:dp(2) = k * (k - 1), dp(3) = k * (k - 1) * (k - 2), dp(1) = 0, dp(0) = k (dp0 和 dp1 是通过 递推方程得到的)
特征方程: x 2 − ( k − 2 ) x − ( k − 1 ) = 0 x^2 - (k - 2)x - (k - 1) = 0 x2−(k−2)x−(k−1)=0
特征根: x 1 = k − 1 , x 2 = − 1 x_1 = k - 1, x_2 = -1 x1=k−1,x2=−1
d p n = A ( k − 1 ) n + B ( − 1 ) n dp_n = A(k - 1)^n + B(-1)^n dpn=A(k−1)n+B(−1)n
解得 A = 1, B = k - 1
那么 d p n = ( k − 1 ) n + ( k − 1 ) ( − 1 ) n , n ≥ 2 dp_n = (k - 1)^n + (k - 1)(-1)^n, n \ge 2 dpn=(k−1)n+(k−1)(−1)n,n≥2
二、神奇的序列
2.1 Catalan 数
2.1.1 认识 Catalan 数
一个栈(无穷大)的进栈序列为1,2,3,…,n有多少个不同的出栈序列?
尝试用递推求解:
定义 f(n) 为 前 n 个元素出栈序列的数目
我们枚举第一次为空的时候已经出栈的元素数目k
那么 f(n) = Σ f(k) * f(n - k),k ∈ [1, n]
n个节点构成的二叉树,共有多少种情形?
同样采用分步递推
定义 f(n) 为 有 n 个节点构成二叉树的数目
枚举左子树节点数目 k
那么 f(n) = Σ f(k) * f(n - k),k ∈ [0, n - 1]
正n边形化分为不重叠的三角形有多少种方法?
其实就是正n 边形的三角剖分数。
我们仍然分步递推

定义 f(n) 为 正n 边形的三角剖分数
设第一次选取 <vn, v1>,三角形左边为 k 边形
那么 f(n) = Σ f(k) * f(n - 1 - k),k ∈ [0, n - 1]
我们发现三个问题有着相同的递推。事实上,上述三个式子都是卡特兰数的递推式。
C(n) = C(0) * C(n - 1) + C(1) * C(n - 2) + … + C(n - 2) * C(1) + C(n - 1) * C(0)
2.1.2 Catalan 数的直接表达式
非降路径问题

从格点(0,0)走到格点(n,n),只能向右或向上走,并且不能越过对角线的路径的条数,就是卡特兰数
如何计算?
不 越过 y = x 等价于 不和 y = x + 1 接触

我们找到和 y = x + 1接触的路径,第一个交叉点后面的路径关于 y = x + 1做对称,那么非法路径的数目相当于 从(0, 0) 出发到达 (n - 1, n + 1)
那么 合法路径的数目为:C(2n, n) - C(2n, n - 1) = 1 n + 1 C ( 2 n , n ) \frac{1}{n + 1}C(2n,n) n+11C(2n,n)
我们尝试母函数求解:
写出卡特兰数 C n = ∑ i = 0 n − 1 C i C n − i − 1 C_n = \sum_{i=0}^{n-1}C_iC_{n-i-1} Cn=∑i=0n−1CiCn−i−1 的母函数
c ( x ) = ∑ n = 0 ∞ C n x n c(x) = \sum_{n=0}^{\infin}C_nx^n c(x)=∑n=0∞Cnxn
c ( x ) 2 = C 0 C 0 + ( C 1 C 0 + C 0 C 1 ) x + ( C 2 C 0 + C 1 C 1 + C 0 C 2 ) x 2 + . . . c(x)^2 = C_0C_0 + (C_1C_0 + C_0C_1)x + (C_2C_0 + C_1C_1 + C_0C_2)x^2 + ... c(x)2=C0C0+(C1C0+C0C1)x+(C2C0+C1C1+C0C2)x2+...
c ( x ) = 1 + x c ( x ) 2 c(x) = 1 + xc(x)^2 c(x)=1+xc(x)2
求解该方程(运用了函数极限和广义二项式定理):

2.1.3 Catalan数的其他实例
-
有2n个人排成一行进入剧场。入场费 5 元。其中只有n个人有一张 5 元钞票,另外 n 人只有 10 元钞票,剧院无其它钞票,问有多少种方法使得只要有 10 元的人买票,售票处就有 5 元的钞票找零?
- 转化为非降路径问题即可
-
Dyck word问题:用Cn表示长度2n的Dyck word 的个数,这里Dyck word是一个有n个X和n个Y组成的字串,且所有的从第一个字符开始的部分字串皆满足X的个数大于等于Y的个数。
- 转化为非降路径问题即可
-
n条线段不相交问题:有n个人围在圆桌参加晚宴,他们两两直接想通过握手相互认识。但是可能影响别人所以他们的手不能有交叉,那么一共有多少种握手的方式?

- 类似于三角剖分的证明
2.2 指数型母函数
二项式定理
(
1
+
x
)
n
=
1
+
n
x
+
n
(
n
−
1
)
2
x
2
+
.
.
.
+
n
(
n
−
1
)
.
.
.
(
n
−
k
+
1
)
k
!
x
k
+
.
.
.
(1+x)^n = 1 + nx + \frac{n(n-1)}{2}x^2 + ... + \frac{n(n-1)...(n-k+1)}{k!}x^k + ...
(1+x)n=1+nx+2n(n−1)x2+...+k!n(n−1)...(n−k+1)xk+...
所以 C(n, k) 的母函数就是
(
1
+
x
)
n
(1 + x)^n
(1+x)n
不禁思考,我们是否可以将排列数P(n, k) 也嵌入到
(
1
+
x
)
n
(1 + x)^n
(1+x)n 中?
(
1
+
x
)
n
=
∑
k
=
0
∞
C
(
n
,
k
)
x
k
=
∑
k
=
0
∞
C
(
n
,
k
)
k
!
k
!
x
k
=
∑
k
=
0
∞
P
(
n
,
k
)
x
k
k
!
\begin{align} (1+x)^n &= \sum_{k=0}^{\infin}C(n,k)x^k \\ &= \sum_{k=0}^{\infin}\frac{C(n,k)k!}{k!}x^k \\ &= \sum_{k=0}^{\infin}P(n,k)\frac{x^k}{k!} \end{align}
(1+x)n=k=0∑∞C(n,k)xk=k=0∑∞k!C(n,k)k!xk=k=0∑∞P(n,k)k!xk
所以,当我们想要用母函数计算排列而非组合数时,应该采用下列的通项,即指数性母函数:
{
1
,
x
,
x
2
2
!
,
.
.
.
,
x
k
k
!
}
\{1,x,\frac{x^2}{2!},...,\frac{x^k}{k!} \}
{1,x,2!x2,...,k!xk}
3个a1,2个a2,3个a3;组成k个数的组合有多少种?
采用 普通母函数 即可计算组合方案数
3个a1,2个a2,3个a3;取4个进行组合,组合的样子?
三个幂级数分别写成x1,x2,x3,相乘后看阶次为4的项的种类
3个a1,2个a2,3个a3;取4个进行排列有多少种?
注意:这不是多重集全排列
我们采用指数型母函数
对于序列a0, a1, a2, …构造一函数:
G ( x ) = a 0 + a 1 x 1 ! + a 2 x 2 2 ! + . . . G(x) = a_0 + a_1\frac{x}{1!} + a_2\frac{x^2}{2!} + ... G(x)=a0+a11!x+a22!x2+...
称函数G(x)是 $a_0, a_1, a_2, … $的指数型母函数。
2.2.1 指数型母函数的应用
计算多重排列
数1出现次数不超过2次,但不能不出现;2出现次数不超过1次;3出现次数可达3次,也可以不出现;4出现次数为偶数
设满足条件的r位数为 a r a_r ar,序列 a 0 , a 1 . … a 10 a_0, a_1.…a_{10} a0,a1.…a10的指数型母函数为
求1,3,5,7,9五个数字组成的n位数的个数, 要求其中3,7出现的次数为偶数,其他1,5,9出现次数不加限制。
2.3 错排
请问n对男女来跳舞,先跳了一曲,下一曲必须换舞伴,请问有多少种不同的换法?
这其实就是经典的欧拉错排问题。
n个有序的元素应有n!个不同的排列,如若一个排列使得所有的元素不在原来的位置上,则称这个排列为错排;有的叫重排
错排的递推关系
123的错排有312,231。这二者可以看作是12错排,3分别与1,2换位而得的。
我们设 n个数 1~n 的错排数目为 D(n)。
那么任取其中一数i,数i分别与其他的n-1个数之一互换,其余n-2个数进行错排,共得 ( n − 1 ) D n − 2 (n-1)D_{n-2} (n−1)Dn−2个错排。
另一部分为 数 i 以外的n-1个数进行错排,然后i与其中每个数互换得 ( n − 1 ) D n − 1 (n-1)D_{n-1} (n−1)Dn−1错排。
其他情况无法一次互换得到
因而 D n = ( n − 1 ) ( D n − 1 + D n − 2 ) m , D 1 = 0 , D 2 = 1 , D 0 = 1 D_n = (n - 1)(D_{n-1} + D_{n-2})m, D_1 = 0, D_2 = 1, D_0 = 1 Dn=(n−1)(Dn−1+Dn−2)m,D1=0,D2=1,D0=1
这是一个非常系数递推关系,下面给出一种解法:


2.4 Stirling 数
2.4.1 第一类Stirling 数
第一类Stirling数 s(n, m) 为 n个人跳集体舞,分成m个圆环的方法数目。
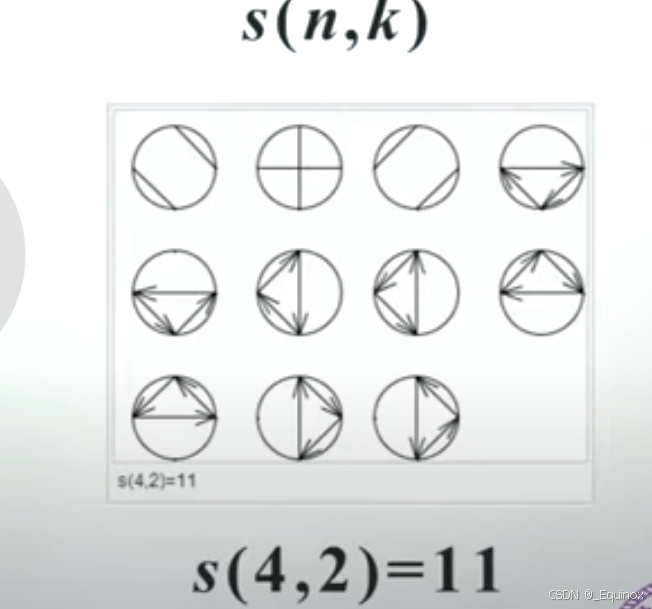
s(n, 0) = 0, s(1, 1) = 1
考虑 n -> n + 1
- 第n+1个人可以单独自己跳舞,其他n个人构成m-1个圈。
- 第n+1个人加入到别的队伍中,可以选择第i个的左边,所以有n个不同的位置,而其他n个人s(n.m)种不同的组圈方法
s(n + 1, m) = s(n, m - 1) + n * s(n, m)
2.4.2 第二类Stirling数
第二类Stirling数S(n, m): n个有区别的球放到m个相同的盒子中,要求无一空盒。

考虑 S(n, m)
- 第n 个球独占一盒,S(n - 1, m - 1)
- 第n 个球放到 前 n - 1 选取的m 个盒子中的其中一个,m * S(n - 1, m)
S(n, m) = S(n - 1, m - 1) + mS(n - 1, m)
如果是 n个有标志的球放进m个有区别的盒子,无空盒:m!S(n, m)
我们尝试用指数型母函数求解第二类Stirling数的直接表达式:












![97,【5】buuctf web [极客大挑战 2020]Greatphp](https://i-blog.csdnimg.cn/direct/bf02989596fa483a90550d39524a3e68.png)