目录
1.红黑树
1.1红黑树的概念
1.2红黑树的性质
1.3红黑树节点的定义
1.4红黑树的插入操作
1.5红黑树的验证
1.6红黑树的删除
1.7红黑树与AVL树的比较
1.8红黑树的应用
1.红黑树
1.1红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
1.2红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
1.3红黑树节点的定义
我们将红色与黑色设置成枚举类型,使代码看起来更加规范,我们定义节点采用类模板的方式,内部成员分别是左节点指针,右节点指针,父亲节点指针,pair结构体类型的变量,然后就是代表我们颜色的变量。我们再对它们进行初始化列表就可以了,我们的每个节点初始颜色都得设置成红色,不然就无法满足我们上面给的5条红黑树的性质。
1.4红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2. 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何 性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连 在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一: cur为红,p为红,g为黑,u存在且为红
cur和p均为红,违反了性质三,此处能否将p直接改为黑?——不能
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
在我们搞清楚了插入的操做的原理之后,我们再来看它的代码就很容易明白了。
//插入 bool Insert(const pair<K, value>& kv) { if (_root == nullptr) { _root = new Node(kv); _root->_col = BLACK; return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { if (kv.first > cur->_kv.first) { parent = cur; cur = cur->_right; } else if (kv.first < cur->_kv.first) { parent = cur; cur = cur->_left; } else { return false; } } cur = new Node(kv); cur->_col = RED; if (kv.first < parent->_kv.first) { parent->_left = cur; } else { parent->_right = cur; } cur->_parent = parent; //调整红黑树 //parent是黑的也直接结束 while (parent && parent->_col == RED) { //关键看叔叔 Node* grandf = parent->_parent; if (parent == grandf->_left) { Node* uncle = grandf->_right; //叔叔存在且为红,变色即可 if (uncle && uncle->_col == RED) { uncle->_col = parent->_col = BLACK; grandf->_col = RED; //继续往上处理 cur = grandf; parent = cur->_parent; } else//叔叔不存在,或则存在且为黑 { // g // p u //c if (cur == parent->_left) { parent->_col = BLACK; grandf->_col = RED; RotateR(grandf); } // g // p u // c else { RotateL(parent); grandf->_col = RED; cur->_col = BLACK; RotateR(grandf); } break; } } else { Node* uncle = grandf->_left; //叔叔存在且为红,变色即可 if (uncle && uncle->_col == RED) { uncle->_col = parent->_col = BLACK; grandf->_col = RED; //继续往上处理 cur = grandf; parent = cur->_parent; } else//叔叔不存在,或则存在且为黑 { // g // u p // c if (cur == parent->_right) { parent->_col = BLACK; grandf->_col = RED; RotateL(grandf); } // g // u p // c else { RotateR(parent); grandf->_col = RED; cur->_col = BLACK; RotateL(grandf); } break; } } } _root->_col = BLACK; return true; }看过我AVL树或则二叉搜索树文章的同学肯定对前半部分代码非常熟悉了,就是二叉搜索树的方式进行插入,接下来我们直接分析红黑树的调整部分的代码。
我们可以看到我们循环的条件是父亲节点不为空且是红的就要一直进行调整,根据我们所画的图,我们需要一个祖父节点,我们发现接下来是有一套if...else,这是判断父亲节点是祖父的左孩子还是右孩子,方便我们确定叔叔节点的位置,我们所画的图只是if的情况,else的情况我没有画的原因是只要你把if的逻辑弄懂了,那么else就是反一下,没有什么新的东西,我等会稍微讲一讲就清楚了,我们重新回到if里,这种情况,叔叔节点就是祖父的右孩子,按照情况一,叔叔存在且为红,那么我们只需要进行变色操作就可以了,如果叔叔不存在,或则存在且为黑,那么我们就需要进行旋转操作,按照情况二的图里,如果cur是在父亲的左子树,那么直接右旋就可以了,不要忘了父亲节点和祖父节点要变色,如果cur是在父亲的右子树方向,那么我们就要进行左旋,变色,再右旋就可以了,跟我们画的图的思路是一模一样的。有了这个思路再看我们else的代码就会发现除了把旋转方向对换一下,指针方向稍微改改,其他可以说是一模一样。
旋转代码:
//右旋 void RotateR(Node* parent) { Node* SubL = parent->_left; Node* SubLR = SubL->_right; parent->_left = SubLR; if (SubLR) { SubLR->_parent = parent; } SubL->_right = parent; Node* ppnode = parent->_parent; parent->_parent = SubL; if (parent == _root) { _root = SubL; _root->_parent = nullptr; } else { if (ppnode->_left == parent) { ppnode->_left = SubL; } else if (ppnode->_right == parent) { ppnode->_right = SubL; } SubL->_parent = ppnode; } }//左旋 void RotateL(Node* parent) { Node* SubR = parent->_right; Node* SubRL = SubR->_left; parent->_right = SubRL; if (SubRL) { SubRL->_parent = parent; } SubR->_left = parent; Node* ppnode = parent->_parent; parent->_parent = SubR; if (parent == _root) { _root = SubR; _root->_parent = nullptr; } else { if (ppnode->_left == parent) { ppnode->_left = SubR; } else if (ppnode->_right == parent) { ppnode->_right = SubR; } SubR->_parent = ppnode; } }右旋和左旋的代码讲解大家可以去看我的C++实现——AVL树那篇文章,这里的左旋右旋代码跟那里的是一模一样的,只不过少了行平衡因子的更新而已,因为红黑树不用平衡因子。
1.5红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
中序遍历代码:
//中序遍历 void InOrder() { _InOrder(_root); } void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->_left); cout << root->_kv.first<< ": " << root->_kv.second << endl; _InOrder(root->_right); }中序遍历就不用我多说什么了吧,就是按照左根右的方式进行递归就可以了。
判断是否是红黑树:
//判断是否平衡 bool IsBalance() { if (_root->_col == RED) { return false; } int refNum = 0; Node* cur = _root; while (cur) { if (cur->_col == BLACK) { refNum++; } cur = cur->_left; } return Check(_root, 0, refNum); } bool Check(Node* root, int blacknum,const int refnum) { if (root == nullptr) { if (refnum != blacknum) { cout << "存在黑色节点不相等的路径" << endl; return false; } return true; } if (root->_col == RED && root->_parent->_col == RED) { cout << root->_kv.first << ": " << "存在红色连续" << endl; return false; } if (root->_col == BLACK) { blacknum++; } return Check(root->_left, blacknum, refnum) && Check(root->_right, blacknum, refnum); }判断是否是红黑树我们要按照它的5条性质去设计。
首先,判断根节点是不是黑的,不是直接返回false,接下来我们再来看其它性质是否满足,我们先计算出一条路径,然后交给check函数去做。
当一条路走完后,我们看一下黑色是不是一样多,一样多我们就返回true,否则返回false。我们还要看是否有连续的红色存在,有就返回false。
最后就是以递归的方式遍历每条路径,遇到黑色节点记录上就好了。
1.6红黑树的删除
红黑树的删除本节不做讲解,有兴趣的同学可参考:《算法导论》或者《STL源码剖析》
推荐博客:http://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html
1.7红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log_2 N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
1.8红黑树的应用
1. C++ STL库 -- map/set、mutil_map/mutil_set
2. Java 库
3. linux内核
4. 其他一些库
C++实现——红黑树
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:/a/871021.html
如若内容造成侵权/违法违规/事实不符,请联系我们进行投诉反馈qq邮箱809451989@qq.com,一经查实,立即删除!相关文章
leetcode67. 二进制求和,简单模拟
leetcode67. 二进制求和
给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。
示例 1: 输入:a “11”, b “1” 输出:“100”
示例 2: 输入:a “1010”, b “1011” 输出:“10101”
…
网络如何发送一个数据包
网络如何发送一个数据包
网络消息发送就是点一点屏幕。 骚瑞,这一点都不好笑。(小品就是我的本质惹) 之前我就是会被这个问题搞的不安宁。是怎么知道对方的IP地址的呢?怎么知道对方的MAC呢?世界上计算机有那么多&…
SQL每日一练-0816
今日SQL题:计算每个项目的年度收入增长率
难度系数:🌟☆☆☆☆☆☆☆☆☆
1、题目要求
计算每个项目每年的收入总额,并计算项目收入环比增长率。找出每年收入增长率最高的项目。输出结果显示年份、项目ID、项目名称、项…
[AHK V2] 转换乱码“涓浗”为“中国”
想还原乱码字符串:涓浗 用乱码恢复工具 乱码恢复 可以查看到,该乱码的现在编码是gbk,原来编码是utf8 (也就是说原来是UTF-8编码的字符串,用GBK编码解析导致产生乱码,那么解析思路就是将GBK编码还原成UTF-8即可 )
编码标识可以在这查阅 代码页标识符
GBK就是cp936
U…
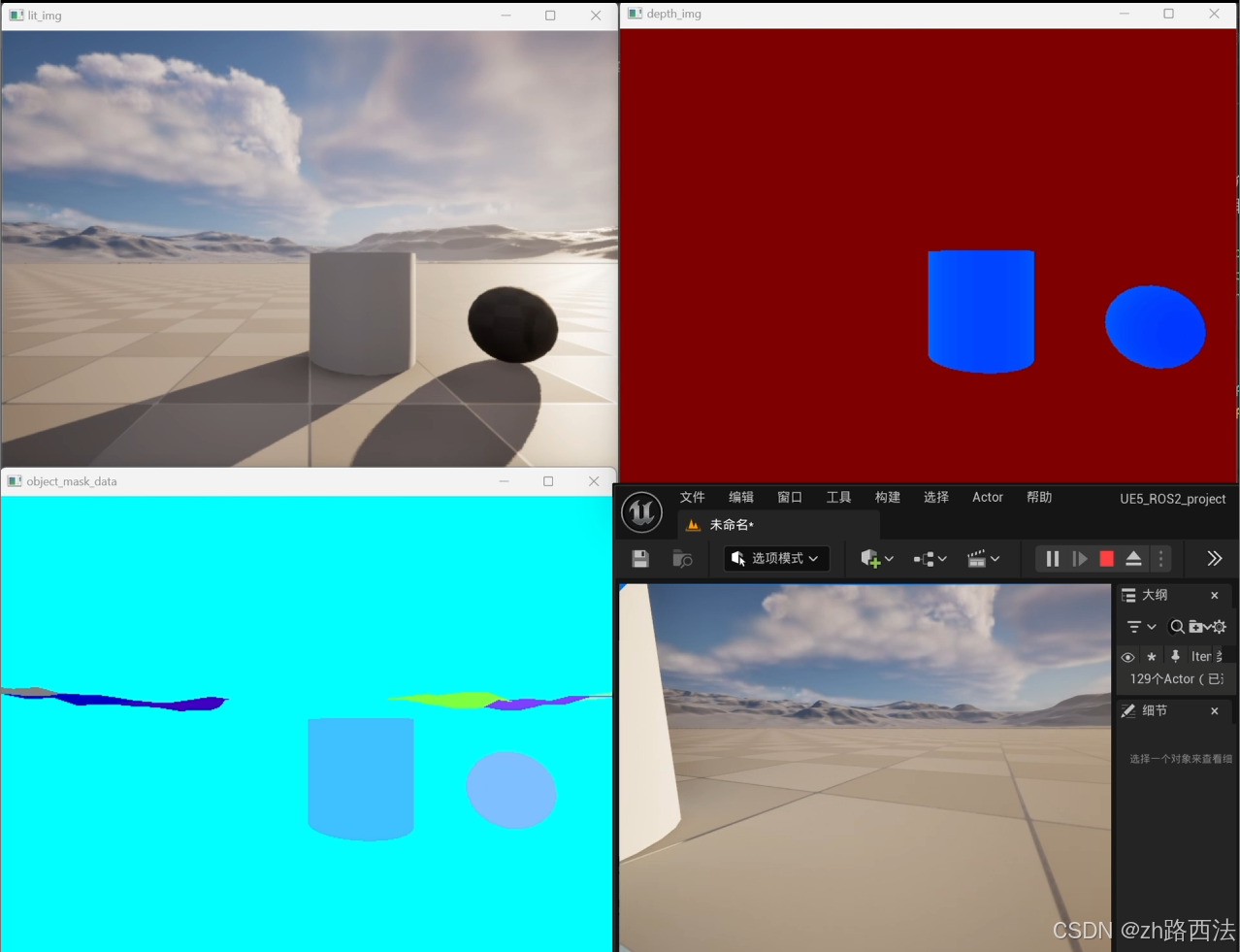
基于UE5和ROS2的激光雷达+深度RGBD相机小车的仿真指南(一)---UnrealCV获取深度+分割图像
前言
本系列教程旨在使用UE5配置一个具备激光雷达深度摄像机的仿真小车,并使用通过跨平台的方式进行ROS2和UE5仿真的通讯,达到小车自主导航的目的。本教程使用的环境: ubuntu 22.04 ros2 humblewindows11 UE5.4.3python8 本系列教程将涉及以…
解决旧版CMS内容管理无法登录的问题
最近遇到了输入正确的账户密码,旧版的CMS内容管理的平台提示登录成功却无法跳转的问题 遇到这种情况请不要慌!!!
请按照下面的步骤解决问题:
1.点击账号管理 2.点击右上角的返回旧版控制台 3.点击cloud1环境 4.点击扩…
leetcode13. 罗马数字转整数,流程图带你遍历所有情况
leetcode13. 罗马数字转整数 示例 1: 输入: s “III” 输出: 3
示例 2: 输入: s “IV” 输出: 4
示例 3: 输入: s “IX” 输出: 9
示例 4: 输入: s “LVIII” 输出: 58 解释: L 50, V 5, III 3.
示例 5: 输入: s “MCMXCIV” 输出: 1994 解释: M 1000, CM 900, XC…
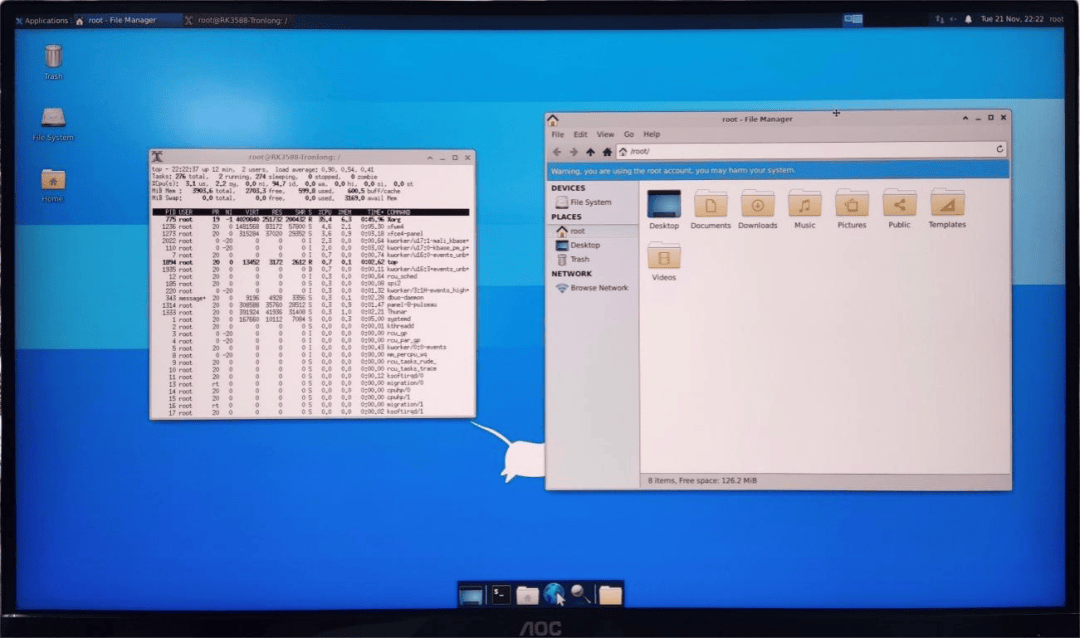
RK3588J正式发布Ubuntu桌面系统,丝滑又便捷!
本文主要介绍瑞芯微RK3588J的Ubuntu系统桌面演示,开发环境如下:
U-Boot:U-Boot-2017.09
Kernel:Linux-5.10.160
Ubuntu:Ubuntu20.04.6
LinuxSDK:
rk3588-linux5.10-sdk-[版本号]
(基于rk3…
Kubectl 常用命令汇总大全
kubectl 是 Kubernetes 自带的客户端,可以用它来直接操作 Kubernetes 集群。 从用户角度来说,kubectl 就是控制 Kubernetes 的驾驶舱,它允许你执行所有可能的 Kubernetes 操作;从技术角度来看,kubectl 就是 Kubernetes…
力扣面试经典算法150题:找出字符串中第一个匹配项的下标
找出字符串中第一个匹配项的下标
今天的题目是力扣面试经典150题中的数组的简单题: 找出字符串中第一个匹配项的下标 题目链接:https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/description/?envTypestudy-plan-v2&envIdto…
知识改变命运 数据结构【栈和队列面试题】
1.最小栈 class MinStack {Stack <Integer>stack;Stack <Integer>minStack; public MinStack() {stacknew Stack<>();minStacknew Stack<>();}public void push(int val) {stack.push(val);if(minStack.empty()) {minStack.push(val);} else {int top…
Android 12系统源码_多屏幕(二)模拟辅助设备功能开关实现原理
前言
上一篇我们通过为Android系统开启模拟辅助设备功能开关,最终实现了将一个Activity显示到多个屏幕的效果。 本篇文章我们具体来分析一下当我们开启模拟辅助设备功能开关的时候,Android系统做了什么哪些操作。
一、模拟辅助设备功能开关应用位置 …
基于web框架的协同过滤的美食推荐系统【数据爬虫、管理系统、数据可更新、样式可调整】
文章目录 有需要本项目的代码或文档以及全部资源,或者部署调试可以私信博主项目介绍研究背景研究的目的与意义协同过滤算法基于用户的协同过滤算法定义基于物品的协同过滤算法的定义 数据库设计db_food(美食信息表)db_collect(美食…
【Kubernetes】k8s集群图形化管理工具之rancher
目录
一.Rancher概述
1.Rancher简介
2.Rancher与k8s的关系及区别
3.Rancher具有的优势
二.Rancher的安装部署
1.实验准备
2.安装 rancher
3.rancher的浏览器使用 一.Rancher概述
1.Rancher简介
Rancher 是一个开源的企业级多集群 Kubernetes 管理平台,实…
【Linux网络】select函数
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 文章目录 select函数介绍select函数参数介绍select函数返回值select的工作流程TCP服务器【多路复用版】 select函数介绍
在Linux网络编程中,select 函数是一种非常有用的IO多路复用技术࿰…
基于springboot的车辆违章信息管理系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…
鸿萌数据恢复服务:SQL Server 中的“PFS 可用空间信息不正确”错误
天津鸿萌科贸发展有限公司从事数据安全服务二十余年,致力于为各领域客户提供专业的数据恢复、数据备份、网络及终端数据安全等解决方案与服务。 同时,鸿萌是国际主流数据恢复软件(Stellar、UFS、R-Studio、ReclaiMe Pro 等)的授权代理商,为专…
RK3568笔记五十六:yolov8_obb旋转框训练部署
若该文为原创文章,转载请注明原文出处。 本文基于rknn_model_zoo和山水无移大佬的博客和代码训练模型并部署到正点原子的ATK-DLRK3568板子测试。
https://github.com/ultralytics/ultralytics 一、训练
1、环境搭建
使用的是AUTODL环境,yolov8-obb数据集不大,也可以使用c…
最新文章
- 在高流量下保持WordPress网站的稳定和高效运行
- linux 安装启动zookeeper全过程及遇到的坑
- langchain系列 - FewShotPromptTemplate 少量示例
- 投资组合风险管理
- MySQL八股学习笔记
- 在windows下安装windows+Ubuntu16.04双系统(下)
- CMU生成式人工智能大模型:从入门到放弃(七)
- 服务拆分的原则
- Spring Boot中的@GetMapping注解可以用于处理HTTP GET请求,并且可以接收对象参数,详细示例
- 《乡村振兴战略下传统村落文化旅游设计 》在2023年畅销榜排名465位
- 【JS重点知识04】JS执行机制(重点面试题)
- 5种常用于LLM的令牌遮蔽技术介绍以及Pytorch的实现









![[AHK V2] 转换乱码“涓浗”为“中国”](https://i-blog.csdnimg.cn/direct/30c1900ddf814697a5d6c694048020e4.png)