第4章 Fouier变换
Raymond Edward Alan Christopher Paley, Fellow of
Trinity College, Cambridge, and International Research
Fellow at the Massachusetts Institute of Technology
and at Harvard University, was killed by an avalanche
on April 7, 1933, while skiing in the vicinity of Banff,
Alberta. Although only twenty-six years of age, he
was already recognized as the ablest of the group of
young English mathematicians who have been inspired
by the genius of G. H. Hardy and J. E. Littlewood. In
a group notable for its brilliant technique, no one had
developed this technique to a higher degree than Paley.
Nevertheless he should not be thought of primarily
as a technician, for with this ability he combined
creative power of the first order. As he himself was
wont to say, technique without “rugger tactics” will
not get one far, and these rugger tactics he practiced
to a degree that was characteristic of his forthright
and vigorous nature.
Possessed of an extraordinary capacity for making
friends and for scientific collaboration, Paley believed
that the inspiration of continual interchange of
ideas stimulates each collaborator to accomplish more
than he would alone. Only the exceptional man works
well with a partner, but Paley had collaborated successfully
with many, including Littlewood, Pólya, Zygmund,and Wiener.
( Raymond Edward Alan Christopher Paley,剑桥三一学院院士、麻省理工学院和哈佛大学国际研究员,于 1933 年 4 月 7 日在Alberta 省 Banff 附近滑雪时遭遇雪崩身亡。虽然只有二十六岁,但他已被公认为受到 G. H. Hardy 和 J. E. Littlewood 天才启发的英国年轻数学家中最有才华的人。在一个以其出色技术而闻名的团队中,没有人比 Paley 将这项技术发展到更高的程度。尽管如此,他不应该被主要视为一名技术人员,因为他凭借这种能力结合了一流的创造力。 正如他自己常说的那样,没有“橄榄球战术”的技术是走不了多远的,而他所练习的这些橄榄球战术达到了他率直而充满活力的性格特征。
Paley 拥有结交朋友和进行科学合作的非凡能力,他相信不断交换思想的灵感会激励每个合作者比他单独完成更多的事情。只有杰出的人才能够与合作伙伴合作得很好,但Paley已经与许多人成功合作,包括Littlewood、Pólya、Zygmund和Wiener。)
------------------------------------------------------------------------------------N. Wiener, 1933
若 f 是 ℝ 上的一个函数,并满足合适的规则和递降条件,则其Fourier变换可定义为
及其逆变换
。
Fourier变换(包括其 d 维变体)在分析中起着基础性作用,正如第 I 册书的读者所领悟的那样。在此,我们想说明 Fourier 变换的一维理论与复分析之间的密切(intimate)而丰富(fruitful)的联系。本章阐述的主旨(The main theme)(表述有些不精确)如下:对于本章开头定义在实轴上的函数 f ,将其扩展成一个全纯函数的可能性与其 Fourier 变换 在无穷远处的寁降(例如指数)密切相关。我们将分两个阶段详细阐述这个主旨。
第一阶段,我们假设 f 可以在包含实轴的水平条中解析连续,并在无穷远处具备“中速递降(moderate decrease)”特性(注:对于一个函数 f ,若它是连续的且存在 A > 0 使得对于任意 x∈ ℝ 有 , 则我们称 f 是中速递降的。一个更为严格的条件是 f ∈ 𝒮 (检测函数的 Schwartz 空间),这也意味着
,更多细节参见第 I 册书),因此,定义 Fourier 变换
的这个积分收敛。因此,我们推断出
在无穷远处是逞指数函数递降的;也直接推断出,对于Fourier 逆变换公式本属性也成立。此外,人们也可以很容易地从这些考量中获得 Poisson求和公式
。顺便说一句,所有这些定理都是周线积分(contour integration)的优雅结果。
第二阶段,我们以Fourier 逆变换公式的有效性作为出发点,若我们假设 和
中速递降的,而无需对 f 的分析性做任何假设,则逆变换公式成立。然后,我们问一个简单而自然的问题:使得 f 的 Fourier 变换在有界区间(比如,[-M,M ])上获得支持的条件是什么?正如人们注意到的那样,这是一个基本问题,无需涉及任何复分析的概念即可表述。然而,仅根据函数 f 的全纯属性即可解决这个问题。条件是(由 Paley-Wiener 定理给出),存在一个 f 的满足以下增长条件的到 ℂ 的全纯扩展:
(对于某个常量 A > 0 ) 。
称满足这个条件的函数为指数型(函数)(exponential type)。
注意观察这个条件, 在紧集合之外消没这种情况可被视为无穷远处的一个递降属性的极端版本,因此,上述定理显然属于上述主题的范围内。
在所有这些问题中,决定性的技术将在于在水平带(strip)(即实轴)的边界内移动积分周线。当 z 具有非零虚部的时候,将利用 的特有行为。事实上,当 z 是实数的时候,指数型函数保持有界且震荡。而若 Im{ z } ≠ 0 ,将有指数递降或递升,取决于是否乘积 ξ Im{ z } 是负数还是正数。
1. 𝕱 类(The class 𝕱)(译注:大写字母 F 的德文尖角体活字)
我们在第I册书中研究Fourier变换时施加到函数上的最弱递降条件是中速递降。在那一章节中,我们在 和
满足
和
( 对于某些正常量 A,A’ 和任意 x,ξ ∈ ℝ)
的条件下证明了 Fourier 逆变换公式和 Poisson 求和公式。引导我们考虑这类函数,因为各种例子(例如 Poisson 核
表明,这类函数在上半平面的稳态热传导方程的 Dirichlet 问题的解中起着基础性的作用。 在Poisson 核这个例子中,我们有 。
在当前的语境下,我们引入一类函数,它特别适用于我们所设立的目标:用复分析证明关于Fourier变换的定理。此外,这类函数足够大,囊括了我们心中很多重要应用的函数。
对于每一个 a > 0 ,我们用 表示满足下列两个条件的所有这类函数 f :
( i ) 函数 f 在水平带(horizontal strip)
中是全纯的。
( i i ) 存在一个常量 A > 0 使得
(对于任意 x∈ ℝ 和 |y| < a ) 。
换句话说, 就是由
上的这些全纯函数构成的,且这些全纯函数在每一个水平轴 Im(z) = y (-a < y < a)上一致地中速递降。例如,对于任意 a ,函数
属于
。
此外,函数
,
其在 z = ±ci 处有简单极点, 对于任意 0 < a < c ,它属于 。
另一个例子是 f (z) = 1/cosh(πz) ,只要| a| < 1/2 ,它就属于 。这个函数及其基本属性之一已经在第3章2.1节例3中讨论过。
也应注意到,Cauchy积分公式的简单应用表明,若 ,则对于每一个 n ,f 的 n阶导数对于任意 b (0 < b < a ) 是属于
的。
最后,我们用 𝕱 表示对于某些 a ,属于 的所有函数类。
评注:
中速递降条件可以稍微弱化,对于任意 ε > 0 ,用 代替
的递降的阶。正如读者所观察到的,在这种限制较少的条件下,下面的许多结果保持不变。
2. 𝕱 上Fourier变换的行为(Action of the Fourier transform on 𝕱)
在此,我们证明有关 𝕱 中函数的三个定理,包括Fourier逆变换和Poisson求和公式。所有这三个证明背后的思想都是相同的:周线积分。因此,所使用的方法将与第I册书中所对应的结果不同。
定理 2.1 若对于某个 a > 0 , f 属于 类,则对于任意 0 ≤ b < a ,有
。
证明:
回顾事实 。b = 0 这种情况只是表明
有界,这一点从定义
的积分公式、f 是中速递降的假设、以及指数函数以 1 为界的事实立即可推出。
现在假设 0 < b < a 及首先假设 ξ > 0 。主要一步为平移积分周线,即,实轴向下移动b的长度。更确切地说,考虑图1中的周线以及函数 。
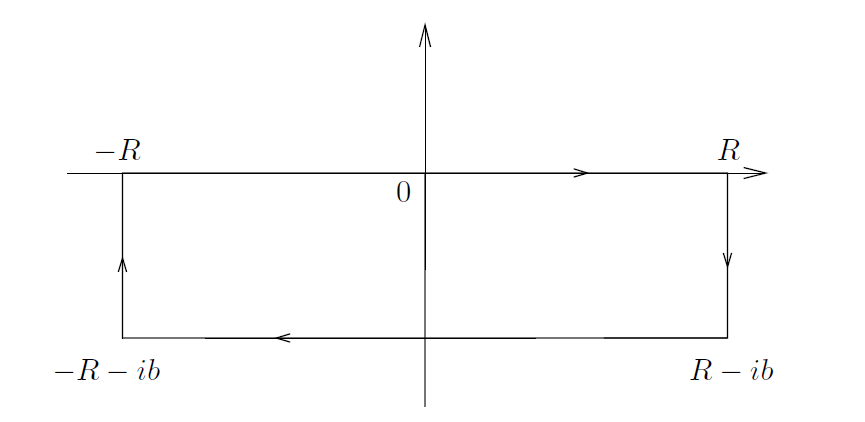
---------------------------------------图1:当 ξ > 0时定理2.1的证明中使用的周线----------------------------
我们断言,随着 R 趋近于无穷大,g在两边垂直边上的积分收敛于0 。例如,左边垂直线段上的积分可以估算为
。
对另一边进行类似的估算证明了我们的断言。因此,通过将Cauchy定理应用于这个大矩形上,当 R 趋近于无穷大时,我们在极限中求得
,
上式导向了估算
,
其中,B 是一个合适的常量。对 ξ < 0 采用相似的论证(只不过这次实轴向上平衡b),就使我们完成了对定理的证明。
这一结论表明,只要 f ∈ 𝕱 ,则 在无穷远处寁降。我们注意到,我们扩展 f 越是 深入(即,加大 a),则我们可选择的 b 可以越大,因此,递降越快。我们将在第 3 节中回到这一循环思想,其中我们所描述的那些函数f 的
具有最终递降条件:紧支持(compact support)。
因为 在ℝ 上寁降,所以Fourier逆变换公式中的积分有意义,现在我们回到这个恒等式的复分析证明。
定理 2.2 若 f ∈ 𝕱 ,则 Fourier 逆变换成立,即
(对于任意 x∈ ℝ) 。
除了周线积分,定理的证明还要求一个简单的恒等式,我们将这个恒等式分开介绍。
引理 2.3 若 A 是一个正数且B是一个实数,则 。
证明:
因为 A > 0 且 B∈ ℝ ,我们有 ,且积分收敛。根据定义
。
然而,
,
上式随着 R 趋近于无穷大而趋近于 1/(A + iB) 。
现在,我们可以证明Fourier 逆变换定理了。再一次地,涉及ξ 的符号问题,因此,首先,我们将Fourier 逆变换公式写成
。
对于第二个积分,我们按后面的方式进行论证。假设f ∈ 𝕱 且选择 0 < b < a 。按定理2.1的证明论证,或者,简单地使用等式(1),我们得到
。
通过应用引理和积分按ξ 的收敛性特性,我们求得
。
其中, 表示从左惯穿到右的直线
。(换句话说,
是实轴向下移动 b 的长度。) 对于 ξ < 0 时的积分,类似的计算给出
。
其中, 是实轴向上移动 b 的长度。现在已知任意 x∈ ℝ ,考虑图2中的周线
。
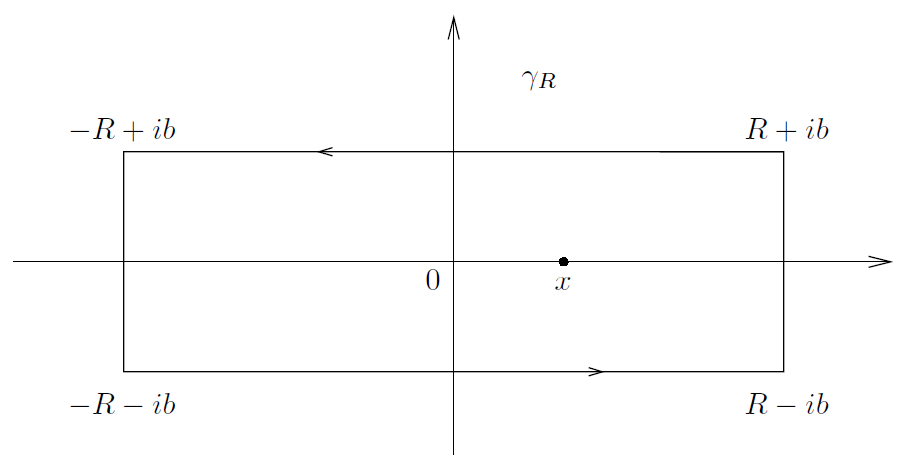
-----------------------------------------------图2: 定理2.2的证明中使用的周线------------------------------------
函数 f ( ζ )/( ζ - x) 在 x 处具有简单极点且具有留数 f ( x ),因此,留数公式给出
。
令 R 趋近于无穷大,读者可以很容易地验证,垂直边上的积分趋近于0,因此,与前面的结果结合在一起,我们得到
。
因此,定理得证。
我们要证明的三个证理中的最后一个是Poisson求和公式。
定理 2.4 若 f ∈ 𝕱 ,则
。
证明:
假设 f ∈ 𝕱 且选择某个 b 使得 0 < b < a 。函数 在整数点具有简单极点且具有留数 1/(2πi ) 。因此,
在整数n处具有简单极点,且具有留数 f ( n )/(2πi )。因此,我们可以将留数公式应用到图3中周线
(其中,N 是整数)。
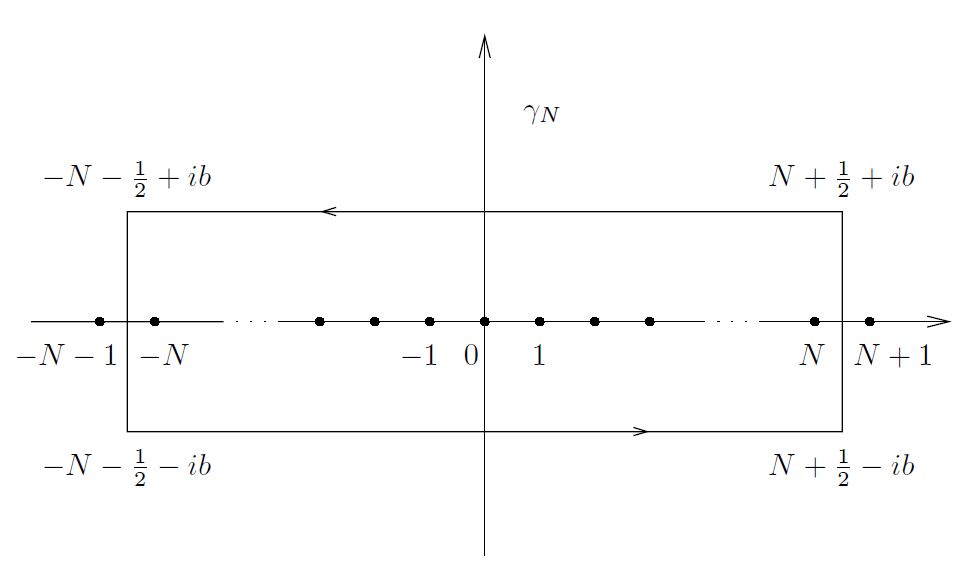
------------------------------------------图3: 定理2.4的证明中使用的周线 ----------------------------
为便产生了
。
令 N 趋向于无穷大,并回顾到,f 具有中速递降特性,我们发现,这个和收敛于 还注意到,垂直线段上的积分趋近于0 。因此,在极限表达式中,我们得到
(2) 。
其中, 和
分别是实数轴向下和向上分别移动b的距离。
现在,我们利用这个事实——若 |w | > 1 ,则
,
可以发现,在 上(其中,
),我们有
。
此外,若 |w| < 1 ,则
,
因此,在 上 ,我们有
。
在(2)中代入这些观察结果,我们求得
,
其中,我们根据等式(1)及其下移的类似物将 和
移回到实数轴。
Poisson求和公式具有许多深远的影响,我们通过推导几个有趣的恒等式来结束本节,这些恒等式对于以后的应用非常重要。
首先,我们回顾第 2 章中例子1中的积分,它表明函数 是其自身的Fourier变换:
。
对于 t > 0 和 a∈ ℝ 的固定值,在上式积分中进行变量替换 表明,函数
是
。将Poisson求和公式应用到Fourier变换对
和
(归属 𝕱 类)上,便产生了下面的关系:
(3) 。
这个恒等式具有显著的影响。例如,其特例 a = 0 是 “θ函数”(theta function)的一个版本的变换法则:若对于 t > 0 , 用级数 定义 𝛝 ,则关系式 (3) 确切地指的是
(4) 。
这个等式将在第6章中用于推导Riemann ζ 函数的关键函数方程。此外,通用格式 a∈ ℝ 将在第10章中用于建立更多一般Jacobi 𝛩 函数的相应法则。
我们所回顾的Poisson求和公式的另一个应用是,我们在第3章例子3中证明函数 1/(cosh(πx)) 的Fourier变换仍然是其自身:
。
这意味着,若 t > 0 和 a∈ ℝ ,则函数 的Fourier 变换是
,应用 Poisson求和公式得到
(5) 。
这个公式将在第 10 章的二平方定理的语境中使用。
3. Paley-Wiener[péili-wí:nə]定理(Paley-Wiener theorem)
在本节,我们稍微改变一下我们的观点:我们不假设 f 的任何分析性,但我们仍假设Fourier逆变换公式的有效性:在条件
和
的条件下,若
, 则有
。对于在这些条件下的逆变换公式的证明,我们建议读者参见第I册第5章。
我们从指出定理 2.1 的部分逆开始。
定理 3.1 假如 对于某两个常量A ,a > 0,满足递降条件
。则对于任意0 < b < a ,则 f (x) 是在带
上全纯的函数 f (z)到ℝ上的限定。
证明:
定义
,
并注意到,根据第2章中的定理5.4 ,则 是复可积函数。此外,还注意到,对于带
中的任意 z ,f (z) 可以定义为
,
因为根据我们在 上的假设,积分绝对收敛:积分优化为
,
上式在 b < a 的情况下是有限的。此外,对于 ,
(随着
),
因此,序列 在
中一致收敛于 f ,根据第 2 章中的定理 5.2 便证明了这个定理。
我们暂时离题,进行如下考察。
推论3.2 若对于某个 a > 0 有 , 且 f 在非空开区间中消没,则 f = 0 。
因为,根据定理,f 在包含实轴的区域上是可分析的,此推论是第2章中定理4.8的一个应用结果。特别是,我们原还了第I册第5章练习21所证明的事实,即,若非 f = 0 ,则 和
不能同时具有紧支持。Paley-Wiener定理比起前面的定理又进了一步,并描述了那些在已知区间[-M,M ]上具有Fourier变换的函数的特征。
定理 3.3 若 f 在ℝ上是连续且中速递降的,则对于某个 A > 0 ,当且仅当其在区间[-M,M ]上具有Fourier变换 时,f 才可以扩展成复平面上具有
的复可积函数。
一个方向的情况简单。若 在区间[-M,M ]被支持,则
和
皆中速递降,且其Fourier逆变换适用公式
。
因为积分域有限,我们可以在积分式中使用复变量 z 替换 x,从而在ℂ上定义复数值函数为
。
若是 z 实数,则按结构 g(z) = f (z),并且根据第2章定理5.4 g是全纯的。最后, 若 z = x + iy ,则我们有
。
相反的结论还需多做一些工作。首先注意到,若 在区间[-M,M ]被支持,则如上论证能给出更强的界限
,而不是我们的假设(即
)。然后,这个思想是试图减少这种更强的界限的情况。然而,这样做是远远不够的,因为我们还需要一个随着 x ⟶ ∞(当 y ≠ 0 时)而呈(中速)递降的函数特性来处理某个积分在无穷远处的收敛性。
因此,我们首先假设 f 的这一进一步的性质,然后我们一步一步地删除额外的假设。
第1步,我们假设 f 在复平面上是全纯的,且满足下列考虑按 x 递降并按 y递增的条件:
(6) 。
然后,我们证明,在这个更强的假设条件下,若 |ξ| > M,则 。为了理解这一点,我们首先假设 ξ > M 并写成
。
此处,我们已经使用标准参数(等式(1))将实轴向下移动 y > 0 的距离。取绝对值给出界限
。
令 y 趋于无穷大,并想到 ξ - M > 0 ,便证明了 。按照类似的论证,将周线向上平移 y > 0 的距离,便证明了只要 ξ < - M ,便有
。第2步,我们放松条件(6),仅假设 f 满足
(7) 。
比起定理中的条件而言,这仍然是一个较强的条件,但比(6)有所减弱。首先假设 ξ > M,对于任意 ε > 0 ,考虑下列辅助函数
。
我们观察到,在闭合的下半平面(包含实轴)中量 具有小于或等于1的绝对值,并随着ε 趋近于0 而趋近于1 。特别是,这证明了随着 ε 趋近于 0 而
,因为我们可以写成
,
并想到,f 在ℝ上中速递降。
但是,对于每个固定的 ε ,我们有
,
因此,根据第1步,我们一定有 , 并因此,随着 ε ⟶ 0 而传递给极限后,有
。尽管我们现在必须在上半平面中论证,并使用
代替 ,但类似的论证适用于ξ < - M 这种情况。
第3步,为了推导出这个证明,只需证明定理中的条件即意味着第2步中的条件(7)即可。事实上,在除以一个恰当的常量之后,只需证明,若对于任意实数x,| f ( x ) | ≤ 1 且对于任意复数 z 有 。这源自Phragmén 和Lindelöf的一个巧妙且非常有用的思想,该思想允许人们将最大模原理应用于各种无界域。我们需要的具体结果如下。
定理 3.4 假设 F 在扇区
中是全纯函数,并且存在常量 C ,c > 0,使得对于扇区中的任意 z ,有 。则对于任意 z∈S,有
| F ( z )| ≤ 1 。
换句话说,若 F 在S 的边界上以 1 为界,且没有更多合理的增长量,则事实上,F 是按1处处有界的。则从简单观察可推断出,在F的增长上施加某种限制是必要的。考虑函数
。在F 在S的边界上以 1 为界,但若 x是实数,则随着 x⟶∞ 而F(x )无界。现在我们给出定理3.4的证明。
证明:
证明思想是“抑制(subdue)”函数 的“敌人(enemy)”,将其变成我们的有利条件:简言之,大家可以修改
, 将其替换成
且 α < 2 。为简单起见,我们取α = 3/2 。
若ε > 0 ,令
。
此处,我们选择对数的主枝来定义 ,因此,若
且 – π < θ < π ,则
。因此,
在 S 中是全纯的,且在其界限内是连续的。此外,
;
且因为在扇区中 – π /4 < θ < π/4 ,我们得到表达式
,
因此,在扇区中,cos(3θ/2) 恒为正值。这与事实 一起,证明了
在闭合扇区中随着
而寁降,特别是,
有界。我们断言,事实上,对于任意
,
( 其中,
表示 S 的闭包 )。为了证明这一点,我们定义
。
假设 F 不等于 0 ,令 为使得
的点序列。因为 M ≠ 0 且
随着 z 在扇区中变得无穷大而递降为 0 ,
不能避开到无穷大,我们推断出这个序列累积到一点
。根据最大值原理,w不会是S的一个内部点,因此,w只能是位于其边界上。但在边界上,我们首先根据假设有 | F(z) | ≤ 1 ,其次根据
,因此 M ≤ 1 ,因此,我们以上的断言得到证明。
最后,我们可以令 ε ⟶ 0 从而推导出定理的证明。
关于Phragmén-Lindelöf 定理的进一步推广,见练习3和问题9。
现在,我们用这个结论来推导 Paley-Wiener 定理的证明,即,证明若 | f (x) | ≤ 1 且 , 则
。首先,注意到,Phragmén-Lindelöf 定理中的扇区可以被旋转,比如,对于第一象限,
,而结果保持不变。则,我们考虑
,
并注意到,F 在正实轴和正虚轴上以 1 为界。此外,因为我们在象限中有 , 我们根据 Phragmén-Lindelöf 定理推导出,对于Q中的任意z ,| F ( z ) | ≤ 1 ,这意味着
。对于其它象限也作类似论证可推导出第3步以及Paley-Wiener 定理的证明。
我们以Paley-Wiener定理背后的另一版本的思想来结束本章,这次描述其Fourier变换对于任意负的ξ 消没的函数。
定理 3.5 假设 和
具有中速递降特性,则对于任意 ξ < 0 ,当且仅当 f 可以在闭合的上半平面
中被延拓成连续有界函数且 f 在其内部是全纯时,
。
证明:
首先假设对于 ξ < 0 有 。根据Fourier逆变换公式
并且,当 z = x + iy 且 y ≥ 0 时,我们可以扩展 f 为
。
注意到积分收敛并且
,
这就证明了 f 的有界性。
在闭合半平面上一致收敛到 f (z) 确立了 f 在这个平面上的连续性和在其内部的全纯性。
对于其逆,我们按照定理3.3的证明的论证思想进行论证。对于正的 ε 和 δ ,我们设
。
则 在包含闭合上半平面的域中是全纯的。我们也可以像之前一样用Cauchy定胆证明,对于任意 ξ < 0 ,
。则,依次传递极限,我们可以得到对于 ξ < 0 有
,最后,对于任意 ξ < 0 ,
。
评注:
读者应该注意到上述定理与第 3 章中的定理 7.1 之间存在一定的类比。这里我们处理的是上半平面中的全纯函数,那里处理的是圆盘中的全纯函数。 在本例中,当ξ < 0 时,Fourier变换消没;而在之前的情况下,当 n < 0 时,Fourier系数消没。
内容来源:
<< Complex Analysis >> ,作者:E.M. Stein & R. Shakarchi
术语参考资料:
<<英汉数学词汇>>,张鸿林,葛显良 编订,清华大学比版社,2018年
<<新英汉数学词汇>> ,科学出版社名词室,科学出版社, 2002年
<<物理学名词>>,第三版,科学出版社会,2019年
<<英汉综合物理学词汇>> 科学出版社,1999年