本讲中将学习如何对角化含有 n 个线性无关特征向量的矩阵，以及对角化是怎样简化计算的。

对角化矩阵 Diagonalizing a matrix S−1AS = Λ

如果矩阵 A 具有 n 个线性无关的特征向量，将它们作为列向量可以组成一个可逆方阵 S，并且有：

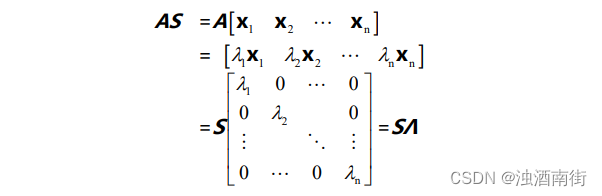
这里的矩阵 Λ 为对角阵，它的非零元素就是矩阵 A 的特征值。因为矩阵 S 中的列向量线性无关，因此逆矩阵 S-1存在。在等式两侧左乘逆矩阵，得到 S-1AS=Λ。同样地，A=SΛS-1。

对于消元法而言，矩阵有 LU 分解，对于施密特正交法，矩阵有 QR 分解，而上面的推导是一种新的矩阵分解。

矩阵的幂 Powers of A

特征值给矩阵的幂计算提供了方法。
如果 Ax=λx，则有 $A^2$x=λAx=${\lambda }^2$x。说明矩阵 $A^2$ 有着和 A 一样的特征向量，而特征值为${\lambda }^2$。我们将写成对角化形式则有：$A^2$=SΛ$S^{-1}$SΛ$S^{-1}$=S${\Lambda }^2$$S^{-1}$。做相同的处理还可以得到：$A^k$ =S${\Lambda }^k$$S^{-1}$。这说明 $A^k$ 有着和 A 一样的特征向量，而特征值为${\lambda }^k$。

如果矩阵 A 具有 n 个线性无关的特征向量，如果所有的特征值均满足 $\left|\begin{array}{c}{\lambda }_i\end{array}\right|$ <1 。则 k→∞时，$A^k$→0。

重特征值 Repeated eigenvalues

如果矩阵 A 没有重特征值，则其一定具有 n 个线性无关的特征向量。
如果矩阵 A 有重特征值，它有可能具有 n 个线性无关的特征向量，也可能没有。比如单位阵的特征值为重特征值 1，但是其具有 n 个线性无关的特征向量。

差分方程 Difference equations $u_{k+1}$=A$u_k$

从给定的一个向量 u0 出发，我们可以通过对前一项乘以矩阵 A 得到下一项的方式，得到一个向量序列：$u_{k+1}$=A$u_k$.

这里的 $u_{k+1}$=A$u_k$可以是一个一阶差分方程，而 $u_k$=$A^k{u}_0$就是方程的解。但这种简洁形式并没有给出足够的信息，我们需要通过特征向量和矩阵的幂运算给出真实解的结构。

斐波那契数列 Fibonacci sequence

斐波那契数列为 0,1,1,2,3,5,8,13……其通项公式为 Fk+2=Fk+1+Fk。求 F100 ？ 如果我们以矩阵的方式来理解数列，则矩阵的特征值可以告诉我们数列中数值的增长速度。
为了凑成矩阵形式，需要用一个比较巧妙的技巧。令 $u_k$ = $\left[\begin{array}{c}a\\ b\end{array}\right]$ ，则有：
$$\begin{array}{rl}& F_{k+2}=F_{k+1}+F_k\\ & F_{k+1}=F_{k+1}\end{array}$$
写成矩阵形式为
$$u_{k+1}=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]u_k$$
观察矩阵 A=$\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]$的特征值和特征向量，因为其为对称矩阵，特征值为实数，且特征向量正交。