Appilied energy论文复现：计及光伏电站快速无功响应特性的分布式电源优化配置方法程序代码！

本程序参考Applied energy论文《Optimal siting and sizing of distributed generation in distribution systems with PV solar farm utilized as STATCOM (PV-STATCOM)》，文中主要对光伏电站、微燃机等分布式电源进行优化配置，程序较为简单和基础，具有较强的可扩展性和适用性，注释清晰，干货满满，下面对文章和程序作简要介绍。

创新点：

1. 在分布式电源的优化配置问题中计及了光伏电站的快速无功响应特性，以体现PV-STATCOM这一新技术对分布式电源配置方案的影响，进而有效响应了近年来因产业升级而日渐增加的敏感负荷的用电需求。

2. 选取了光伏电站、微型燃气轮机两种典型的分布式电源进行优化配置问题的研究，通过构建加权电压支撑能力指标以表征配电系统中光伏电站对敏感负荷节点的电压支撑能力，并将其嵌入到分布式电源优化配置模型中以求解最优的分布式电源安装位置和安装容量，以及对应的电压暂降过程仿真，充分证明了本研究的价值和意义。

文中结果：

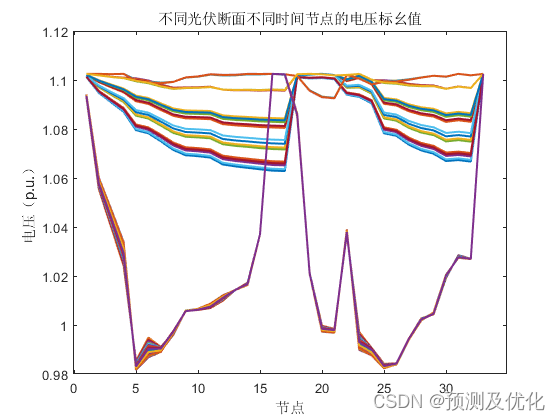
程序结果：

部分程序：

%计算电压支撑能力指标
% Program for Newton-Raphson Load Flow Analysis..
nbus = 33;                  
mpc=IEEE33BW;
T=24;
nb=33;
nl=32;
N=5;%光伏断面数量
Wref=0;%电力支撑指标下限
pref=0;%光伏渗透率约束下限
rmt=0.0001;%微燃机出力下限
dw_pv=[1 3 8 5 2];%每个光伏区间单位光伏有功出力
Y =[8.60890545517020 - 4.38848759645336i,-8.60890545517020 + 4.38848759645336i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 00.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-0.675684973458593 + 0.889394050182110i,1.61983928437771 - 1.72970736243838i,-0.944154310919121 + 0.840313312256273i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.638181753905898i,1.15270060498254 - 1.01042169531650i,-0.278801443624791 + 0.372239941410601i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,-3.19139102810467 + 3.04544326767306i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.000.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-0.685901016646612 + 0.541617384080303i,1.37813650857855 - 1.08327620483196i,-0.692235491931937 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-0.692235491931937 + 0.541658820751653i,0.692235491931937 - 0.541658820751653i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-3.91132581228411 + 1.99227137433585i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-2.79428122129950 + 1.42270405602406i,3.32556722153864 - 1.89112873819902i,-0.531286000239134 + 0.468424682174957i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.0007 + 0.615869856836191i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.0000.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000.513100757068179i,1.88471913450910 - 2.10469649825879i,-1.36554428748186 + 1.59159574119061i,0.00000000000000 + 0.00000000000000i;0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,0.00000000000000 + 0.00000000000000i,-0.858092532269815 + 1.33419548565823i,0.858092532269815 - 1.33419548565823i];          % Calling ybusppg.m to get Y-Bus Matrix..
busd =[1,1,1,0,0,0,0,0,0,0;
    2,3,1,0,0,0,0.100000000000000,0.0600000000000000,0,0;
    3,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    4,3,1,0,0,0,0.120000000000000,0.0800000000000000,0,0;
    5,3,1,0,0,0,0.0600000000000000,0.0300000000000000,0,0;
    6,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    7,3,1,0,0,0,0.200000000000000,0.100000000000000,0,0;
    8,3,1,0,0,0,0.200000000000000,0.100000000000000,0,0;
    9,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    10,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    11,3,1,0,0,0,0.0450000000000000,0.0300000000000000,0,0;
    12,3,1,0,0,0,0.0600000000000000,0.0350000000000000,0,0;
    13,3,1,0,0,0,0.0600000000000000,0.0350000000000000,0,0;
    14,3,1,0,0,0,0.120000000000000,0.0800000000000000,0,0;
    15,3,1,0,0,0,0.0600000000000000,0.0100000000000000,0,0;
    16,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    17,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    18,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    19,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    20,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    21,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    22,3,1,0,0,0,0.0900000000000000,0.0400000000000000,0,0;
    23,3,1,0,0,0,0.0900000000000000,0.0500000000000000,0,0;
    24,3,1,0,0,0,0.420000000000000,0.200000000000000,0,0;
    25,3,1,0,0,0,0.420000000000000,0.200000000000000,0,0;
    26,3,1,0,0,0,0.0600000000000000,0.0250000000000000,0,0;
    27,3,1,0,0,0,0.0600000000000000,0.0250000000000000,0,0;
    28,3,1,0,0,0,0.0600000000000000,0.0200000000000000,0,0;
    29,3,1,0,0,0,0.120000000000000,0.0700000000000000,0,0;
    30,3,1,0,0,0,0.200000000000000,0.600000000000000,0,0;
    31,3,1,0,0,0,0.150000000000000,0.0700000000000000,0,0;
    32,3,1,0,0,0,0.210000000000000,0.100000000000000,0,0;
    33,3,1,0,0,0,0.0600000000000000,0.0400000000000000,0,0];      % Calling busdatas..
BMva = 100;                 % Base MVA..
bus = busd(:,1);            % Bus Number..
type = busd(:,2);           % Type of Bus 1-Slack, 2-PV, 3-PQ..
V = busd(:,3);              % Specified Voltage..
del = busd(:,4);            % Voltage Angle..
    Pg = busd(:,5)/BMva;        % PGi..
    Qg = busd(:,6)/BMva;        % QGi..
    Pl = busd(:,7)/BMva;        % PLi..
    Ql = busd(:,8)/BMva;        % QLi..
    Qmin = busd(:,9)/BMva;      % Minimum Reactive Power Limit..
    Qmax = busd(:,10)/BMva;     % Maximum Reactive Power Limit..
P = Pg - Pl;                % Pi = PGi - PLi..
Q = Qg - Ql;                % Qi = QGi - QLi..
Psp = P;                    % P Specified..
Qsp = Q;                    % Q Specified..
G = real(Y);                % Conductance matrix..
B = imag(Y);                % Susceptance matrix..

pv = find(type == 2 | type == 1);   % PV Buses..
pq = find(type == 3);               % PQ Buses..
npv = length(pv);                   % No. of PV buses..
npq = length(pq);                   % No. of PQ buses..

Tol = 1;  
Iter = 1;
while (Tol > 1e-5)  % Iteration starting..
    
    P = zeros(nbus,1);
    Q = zeros(nbus,1);
    % Calculate P and Q
    for i = 1:nbus
        for k = 1:nbus
            P(i) = P(i) + V(i)* V(k)*(G(i,k)*cos(del(i)-del(k)) + B(i,k)*sin(del(i)-del(k)));
            Q(i) = Q(i) + V(i)* V(k)*(G(i,k)*sin(del(i)-del(k)) - B(i,k)*cos(del(i)-del(k)));
        end
    end

    % Checking Q-limit violations..
    if Iter <= 7 && Iter > 2    % Only checked up to 7th iterations..
        for n = 2:nbus
            if type(n) == 2
                QG = Q(n)+Ql(n);
                if QG < Qmin(n)
                    V(n) = V(n) + 0.01;
                elseif QG > Qmax(n)
                    V(n) = V(n) - 0.01;
                end
            end
         end
    end
    
    % Calculate change from specified value
    dPa = Psp-P;
    dQa = Qsp-Q;
    k = 1;
    dQ = zeros(npq,1);
    for i = 1:nbus
        if type(i) == 3
            dQ(k,1) = dQa(i);
            k = k+1;
        end
    end
    dP = dPa(2:nbus);
    M = [dP; dQ];       % Mismatch Vector
    
    % Jacobian
    % J1 - Derivative of Real Power Injections with Angles..
    J1 = zeros(nbus-1,nbus-1);
    for i = 1:(nbus-1)
        m = i+1;
        for k = 1:(nbus-1)
            n = k+1;
            if n == m
                for n = 1:nbus
                    J1(i,k) = J1(i,k) + V(m)* V(n)*(-G(m,n)*sin(del(m)-del(n)) + B(m,n)*cos(del(m)-del(n)));
                end
                J1(i,k) = J1(i,k) - V(m)^2*B(m,m);
            else
                J1(i,k) = V(m)* V(n)*(G(m,n)*sin(del(m)-del(n)) - B(m,n)*cos(del(m)-del(n)));
            end
        end
    end
    
    % J2 - Derivative of Real Power Injections with V..
    J2 = zeros(nbus-1,npq);
    for i = 1:(nbus-1)
        m = i+1;
        for k = 1:npq
            n = pq(k);
            if n == m
                for n = 1:nbus
                    J2(i,k) = J2(i,k) + V(n)*(G(m,n)*cos(del(m)-del(n)) + B(m,n)*sin(del(m)-del(n)));
                end
                J2(i,k) = J2(i,k) + V(m)*G(m,m);
            else
                J2(i,k) = V(m)*(G(m,n)*cos(del(m)-del(n)) + B(m,n)*sin(del(m)-del(n)));
            end
        end
    end
    
    % J3 - Derivative of Reactive Power Injections with Angles..
    J3 = zeros(npq,nbus-1);
    for i = 1:npq
        m = pq(i);
        for k = 1:(nbus-1)
            n = k+1;
            if n == m
                for n = 1:nbus
                    J3(i,k) = J3(i,k) + V(m)* V(n)*(G(m,n)*cos(del(m)-del(n)) + B(m,n)*sin(del(m)-del(n)));
                end
                J3(i,k) = J3(i,k) - V(m)^2*G(m,m);
            else
                J3(i,k) = V(m)* V(n)*(-G(m,n)*cos(del(m)-del(n)) - B(m,n)*sin(del(m)-del(n)));
            end
        end
    end

欢迎感兴趣的小伙伴关注下方公众号获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：/a/237860.html

如若内容造成侵权/违法违规/事实不符，请联系我们进行投诉反馈qq邮箱809451989@qq.com，一经查实，立即删除！

相关文章

SD生成的图像不清晰，如何解决

SD生成的图像不清晰，如何解决

文生图 选择高清修复&#xff1a; 几点注意 重绘幅度&#xff1a;这里不用太高&#xff0c;他会根据你生成的低分辨率图像&#xff0c;生成高分辨率的图像&#xff0c;可以选择0.3~05之间&#xff0c;给AI跟多想象力空间可以选择0.5 ~ 0.7。太低边缘模糊&#xff0c;太高了可能…
阅读更多...
《数字图像处理-OpenCV/Python》连载（56）图像的灰度直方图

《数字图像处理-OpenCV/Python》连载（56）图像的灰度直方图

《数字图像处理-OpenCV/Python》连载&#xff08;56&#xff09;非线性灰度变换 本书京东 优惠购书链接 https://item.jd.com/14098452.html 本书CSDN 独家连载专栏 https://blog.csdn.net/youcans/category_12418787.html 第 8 章 图像的直方图处理 图像的直方图是反映像素值…
阅读更多...
约瑟夫问题

约瑟夫问题

目录 方法一&#xff1a;数组模拟 方法二&#xff1a;链表模拟 方法三&#xff1a;数学递归 约瑟夫问题&#xff1a; 编号为 1 到 n 的 n 个人围成一圈。从编号为 1 的人开始报数&#xff0c;报到 m 的人离开。下一个人继续从 1 开始报数。 n-1 轮结束以后&#xff0c;只剩下…
阅读更多...
人人都能用的AI编程助手 CodeGeeX

人人都能用的AI编程助手 CodeGeeX

视频版&#xff1a;人人都能用的Ai编程助手——CodeGeeX 大家好&#xff0c;我是凌览。 现在距离 AI 大火已经快有一年啦&#xff0c;作为程序员可不得准备一款AI帮咱们干点活。本文分享一款 AI 工具 CodeGeeX&#xff0c;帮助大家提高一波学习和工作效率。 CodeGeeX 是什么…
阅读更多...
Linux之Apache服务器安装及配置

Linux之Apache服务器安装及配置

一、Apache服务器简介 Apache HTTP Server&#xff08;简称Apache&#xff09;是Apache软件基金会的一个开放源码的网页服务器&#xff0c;可以在大多数计算机操作系统中运行&#xff0c;由于其多平台和安全性被广泛使用。Apache曾经是世界使用排名第一的Web服务器软件&#xf…
阅读更多...
strict-origin-when-cross-origin

strict-origin-when-cross-origin

严格限制同源策略 &#xff08;1&#xff09;允许服务器的同源IP地址访问 &#xff08;2&#xff09;允许Referer --- 后端服务器要配置
阅读更多...
两线制 4-20mA 隔离变送器(输出回路供电)

两线制 4-20mA 隔离变送器(输出回路供电)

两线制 4-20mA 隔离变送器(输出回路供电) 特征&#xff1a; ◆低成本&#xff0c;小体积&#xff0c;符合 UL94-V0 阻燃标准 ◆安装方式采用国际标准 DIN35mm 导轨安装方式 ◆双隔离(信号输入、信号输出相互之间 3000VDC 隔离) ◆4-20mA 电流输入与输出&#xff0c;精度高(失真…
阅读更多...
ansible部署安装Tomcat

ansible部署安装Tomcat

我们需要用到的文件jdk以及tomcat安装包 下载链接:https://pan.baidu.com/s/1sjG8Yl8k-SUbOv7KwKXZMA 提取码&#xff1a;t71z 准备n台机器&#xff08;我这里就简单部署三台机器&#xff09; ansible的安装部署以及配置可以看博主之前的文章自动化运维工具-ansible部署 ansib…
阅读更多...
zookeeper高级应用原理

zookeeper高级应用原理

文章目录 分布式锁分布式锁-读写锁分布式锁-Curator实现ZK集群管理 zookeeper 集群zookeeper 集群节点个数配置zookeeper 选举ZAB协议zookeeper 选举zookeeper 集群数据读写 分布式锁 分布式锁&#xff1a;在分布式环境下&#xff0c;保护跨进程、跨主机、跨网络的共享资源&am…
阅读更多...
Day57力扣打卡

Day57力扣打卡

打卡记录 最小体力消耗路径 链接 Dijkstra 将Dijkstra算法从计算最短路径转化为计算路径最大差值。 class Solution:def minimumEffortPath(self, heights: List[List[int]]) -> int:n, m len(heights), len(heights[0])dist [0] [0x3f3f3f3f] * (n * m - 1)vis set…
阅读更多...
iPhone 数据恢复:iMyFone D-Back iOS

iPhone 数据恢复:iMyFone D-Back iOS

iMyFone D-Back iOS 最佳 iPhone 数据恢复&#xff0c;最好的 iPhone 数据恢复软件&#xff0c;恢复成功率最高。 直接从iOS设备、iTunes/iCloud/第三方程序备份快速恢复数据。 有选择地恢复已删除的照片、WhatsApp、消息和 18 多种其他数据类型。 仅通过 iCloud 帐户访问即可从…
阅读更多...
【组合数学】递推关系

【组合数学】递推关系

目录 1. 递推关系建立2. 常系数齐次递推关系的求解3. 常系数非齐次递推关系的求解4. 迭代法 1. 递推关系建立 给定一个数的序列 f ( 0 ) , f ( 1 ) , . . . , f ( n ) , . . . , f (0), f(1), ..., f(n ),... , f(0),f(1),...,f(n),..., 若存在整数 n 0 n_0 n0​ &#xff…
阅读更多...
启动jar包命令

启动jar包命令

一、Windows环境 找到jar包的位置&#xff1b; 按shift键&#xff0c;点击鼠标右键&#xff0c;选中在此处打开PowerShell窗口&#xff1b; 此时进入命令行工具 输入java -jar .\java_web-0.0.1-SNAPSHOT.jar&#xff08;注意空格&#xff09;。 二、Linux环境 2.1 方式一 …
阅读更多...
【二者区别】cuda和cudatoolkit

【二者区别】cuda和cudatoolkit

Pytorch 使用不同版本的 cuda 由于课题的原因&#xff0c;笔者主要通过 Pytorch 框架进行深度学习相关的学习和实验。在运行和学习网络上的 Pytorch 应用代码的过程中&#xff0c;不少项目会标注作者在运行和实验时所使用的 Pytorch 和 cuda 版本信息。由于 Pytorch 和 cuda 版…
阅读更多...
【JVM从入门到实战】（二）字节码文件的组成

【JVM从入门到实战】（二）字节码文件的组成

一、Java虚拟机的组成 二、字节码文件的组成 字节码文件的组成 – 应用场景 字节码文件的组成部分-Magic魔数 什么是魔数&#xff1f; Java字节码文件中的魔数 文件是无法通过文件扩展名来确定文件类型的&#xff0c;文件扩展名可以随意修改&#xff0c;不影响文件的内容。…
阅读更多...
用23种设计模式打造一个cocos creator的游戏框架----(十三)模板方法模式

用23种设计模式打造一个cocos creator的游戏框架----(十三)模板方法模式

1、模式标准 模式名称&#xff1a;模板方法模式 模式分类&#xff1a;行为型 模式意图&#xff1a;定义一个操作中的算法骨架&#xff0c;而将一些步骤延迟到子类中。Template Method 使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 结构图&#xff1a…
阅读更多...
【ArcGIS Pro微课1000例】0053：基于SQL Server创建与启用地理数据库

【ArcGIS Pro微课1000例】0053：基于SQL Server创建与启用地理数据库

之前的文章有讲述基于SQL Server创建企业级地理数据库，本文讲述在SQL Server中创建常规的关心数据库，然后在ArcGIS Pro中将其启用，转换为企业级地理数据库。 1. 在SQL Server中创建数据库** 打开SQL Server 2019，连接到数据库服务器。 展开数据库连接，在数据库上右键→新…
阅读更多...
使用Android Studio的Gradle Tasks对源码生成jar包

使用Android Studio的Gradle Tasks对源码生成jar包

一. 前言 As工具可以用来编译第三方源码&#xff08;比如okhttp &#xff0c;retrofit源码&#xff09;&#xff0c; 用于打jar包或aar包&#xff0c;使用工具自带的Tasks工具可以帮忙我们完成这些事情。 二. 遇到问题 Android Studio Gradle打包Tasks不显示&#xff0c;如图…
阅读更多...
销售技巧培训之如何提升房地产销售技巧

销售技巧培训之如何提升房地产销售技巧

在房地产销售这个竞争激烈的行业中&#xff0c;要想获得成功&#xff0c;不仅需要熟练掌握销售技巧&#xff0c;还需要不断地提升自己的能力。下面&#xff0c;我们将从以下几个方面探讨如何提升房地产销售技巧。 一、了解客户需求 倾听客户&#xff1a;在与客户沟通时&#x…
阅读更多...
正运动ZDevelop软件使用流程

正运动ZDevelop软件使用流程

ZDevelop是正运动技术ZMoiton系列运动控制器的PC端程序开发调试与诊断软件&#xff0c;通过它用户能够很容易的对控制器进行程序编辑与配置&#xff0c;快速开发应用程序、实时诊断系统运行参数以及对运动控制器正在运行的程序进行实时调试&#xff0c;支持中英双语环境。 BAS…
阅读更多...
最新文章

Copyright @ 2022~2023