Linear independent component analysis (ICA)
x i ( k ) = ∑ j = 1 n a i j s j ( k ) for all i = 1 … n , k = 1 … K ( ) x_i(k) = \sum_{j=1}^{n} a_{ij}s_j(k) \quad \text{for all } i = 1 \ldots n, k = 1 \ldots K \tag{} xi(k)=j=1∑naijsj(k)for all i=1…n,k=1…K()
- x i ( k ) x_i(k) xi(k) is the i i i-th observed signal in sample point k k k (possibly time)
- a i j a_{ij} aij constant parameters describing “mixing”
- Assuming independent, non-Gaussian latent “sources” s j s_j sj
- ICA is identifiable, i.e. well-defined. Observing only x i x_i xi we can recover both a i j a_{ij} aij and s j s_j sj .
Fundamental difference between ICA and PCA
- PCA doesn’t find the original coordinates, ICA does.
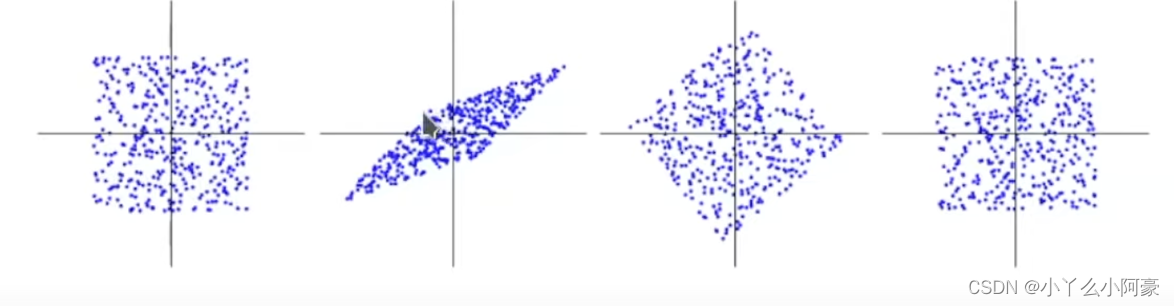
- PCA, Gaussian factor analysis are not identifiable:
- Any orthogonal rotation is equivalent: s ′ = U s s' = Us s′=Us has same distribution.
Nonlinear ICA is an unsolved problem
-
Extend ICA to nonlinear case to get general disentanglement?
-
Unfortunately, “basic” nonlinear ICA is not identifiable:
-
If we define nonlinear ICA model for random variables ( x_i ) as
x i = f i ( s 1 , … , s n ) , i = 1 … n x_i = f_i(s_1, \ldots, s_n) , i = 1 \ldots n xi=fi(s1,…,sn),i=1…n
we cannot recover original sources (Darmois, 1952; Hyvärinen & Pajunen, 1999)
Darmois construction
-
Darmois (1952) showed the impossibility of nonlinear ICA:
-
For any x 1 , x 2 x_1, x_2 x1,x2, can always construct y = g ( x 1 , x 2 ) y = g(x_1, x_2) y=g(x1,x2) independent of x 1 x_1 x1 as
g ( ξ 1 , ξ 2 ) = P ( x 2 < ξ 2 ∣ x 1 = ξ 1 ) g(\xi_1, \xi_2) = P(x_2 < \xi_2 | x_1 = \xi_1) g(ξ1,ξ2)=P(x2<ξ2∣x1=ξ1)
-
Independence alone too weak for identifiability:
- We could take x 1 x_1 x1 as an independent component which is absurd
-
Looking at non-Gaussianity equally absurd:
- Scalar transform h ( x 1 ) h(x_1) h(x1) can give any distribution
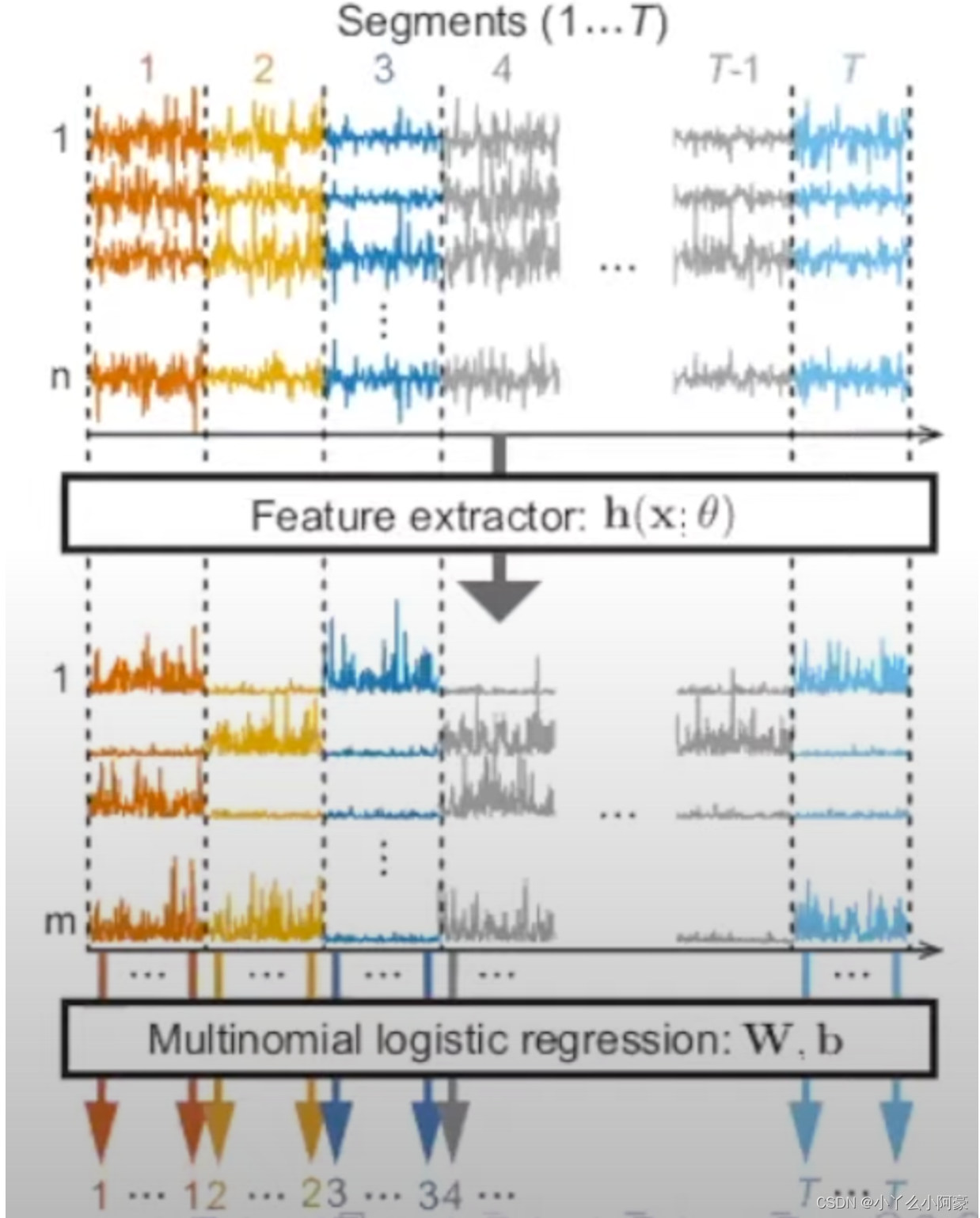
Time-contrastive learning
- Observe n n n-dim time series x ( t ) x(t) x(t)
- Divide x ( t ) x(t) x(t) into T T T segments (e.g., bins with equal sizes)
- Train MLP to tell which segment a single data point comes from
- Number of classes is T T T
- Labels given by index of segment
- Multinomial logistic regression
- In hidden layer h h h, NN should learn to represent nonstationarity 非平稳性 (= differences between segments)
- Could this really do Nonlinear ICA?
- Assume data follows nonlinear ICA model
x
(
t
)
=
f
(
s
(
t
)
)
x(t) = f(s(t))
x(t)=f(s(t)) with
- smooth, invertible nonlinear mixing f : R n → R n f : \mathbb{R}^n \rightarrow \mathbb{R}^n f:Rn→Rn
- components s i ( t ) s_i(t) si(t) are nonstationary, e.g., in variances
- Assume we apply time-contrastive learning on
x
(
t
)
x(t)
x(t)
- using MLP with hidden layer in h ( x ( t ) ) h(x(t)) h(x(t)) with dim ( h ) = dim ( x ) \text{dim}(h) = \text{dim}(x) dim(h)=dim(x)
- Then, TCL will find s ( t ) 2 = A h ( x ( t ) ) s(t)^2 = Ah(x(t)) s(t)2=Ah(x(t)) for some linear mixing matrix A A A. (Squaring is element-wise)
- I.e.: TCL demixes nonlinear ICA model up to linear mixing (which can be estimated by linear ICA) and up to squaring.
- This is a constructive proof of identifiability
- Imposing independence at every segment -> more constraints -> unique solution. 增加了限制保证了indentifiability
用MLP,通过自监督分类(某一个信号来自于哪个时间段)来训练网络。这样MLP可以表示不同时间段内的信号差。而后原始信号 s 2 s^2 s2 可以表示为观测值(x)经MLP隐藏层分离结果的线性组合。
Deep Latent Variable Models
-
General framework with observed data vector x x x and latent s s s:
p ( x , s ) = p ( x ∣ s ) p ( s ) , p ( x ) = ∫ p ( x , s ) d s p(x, s) = p(x|s)p(s), \quad p(x) = \int p(x, s)ds p(x,s)=p(x∣s)p(s),p(x)=∫p(x,s)ds
where θ \theta θ is a vector of parameters, e.g., in a neural network -
In variational autoencoders (VAE):
- Define prior so that s s s white Gaussian (thus s i s_i si; all independent)
- Define posterior so that x = f ( s ) + n x = f(s) + n x=f(s)+n
-
Looks like Nonlinear ICA, but not identifiable
- By Gaussianity, any orthogonal rotation is equivalent:
s ′ = M s has exactly the same distribution if M T M = I s' = Ms \text{ has exactly the same distribution if } M^TM = I s′=Ms has exactly the same distribution if MTM=I
- By Gaussianity, any orthogonal rotation is equivalent:
Conditioning DLVM’s by another variable
通过引入一个新的变量u来解,比如找视频和音频的关系,时间t就可以作为辅助变量(auxiliary varibale)。通过条件独立(conditional independent)来解。
Conclusion
-
Typical deep learning needs class labels, or some targets
-
If no class labels: unsupervised learning
-
Independent component analysis is a principled approach
- can be made nonlinear
-
Identifiable: Can recover components that actually created the data (unlike PCA, VAE etc)
-
Special assumptions needed for identifiability, one of:
- Nonstationarity (“time-contrastive learning”)
- Temporal dependencies (“permutation-contrastive learning”)
- Existence of auxiliary (conditioning) variable (e.g., “iVAE”)
-
Self-supervised methods are easy to implement
-
Connection to DLVM’s can be made → iVAE
-
Principled framework for “disentanglement”
总结来说Linear ICA是可解的,对于Nonlinear ICA则需要增加额外的假设才能可解(原始信号可分离)。Nonlinear ICA的思想可以用在深度学习的其他模型上。
Reference
- https://www.youtube.com/watch?v=_cBLSNRWt8c