容斥dp，二项式反演

前言

由于水平有限，这篇文章比较难懂，并且也有很多不够透彻的地方，如果您有任何的看法，非常感谢您私信指导。

容斥dp

用dp的方法来描述容斥，大概的想法是，把容斥系数分到每一步里去乘。

通常当你有容斥做法，且适配的子集条件较为一般，且数据范围不足通过时考虑使用容斥dp。

确实不太好描述，看题吧。

来源神秘

求长度为 $n\leq 2000$ ，值域为 $m\leq 2000$ 的序列个数，满足前一个数不是后一个数的非本身的倍数。

设 $f_{i,j}$ 表示前 $i$ 个数，第 $i$ 个数为 $j$ 的合法序列方案数，则：
$f_{i,j}=\underset{k=1}{\overset m\sum}[j=k 或 j\nmid k]f_{i-1,k}$
复杂度 $O(nm^2)$

如果我们转化成：
$f_{i,j}=\underset{k=1}{\overset m\sum}f_{i-1,k}-\underset{k=1}{\overset m\sum}[j\not=k 且 j\mid k]f_{i-1,k}$

就可以做到 $O(nm\log m)$

$n,m\leq 10^5$ ：
考虑容斥，如果设 $S_i$ 表示第 $i, i + 1$ 个数满足限制的所有方案构成的集合，那么答案为 $|\bigcap S_i|$ ，那么其补集为一些数不满足限制，也就是说是倍数关系。如果设 $f (i)$ 表示 $i$ 选出 $i$ 个位置不满足条件的方案数，设 $g (i)$ 表示恰好 $n$ 中有 $i$ 个位置不满足条件的方案数，那么相当于二项式反演的式子（虽然可以直接认为是容斥，但是虽然但是）：
$f(x)=\underset{i=x}{\overset n\sum}\begin{pmatrix}i\\x\end{pmatrix}g(i)$
$g(x)=\underset{i=x}{\overset n\sum}\begin{pmatrix}i\\x\end{pmatrix}(-1)^{i-x}f(i)$
$ans=g(0)=\underset{i=0}{\overset n\sum}(-1)^if(i)$

我们可以认为一个不合法的相邻位置会贡献一个 $- 1$ 的容斥系数，具体来说会给它这种方案乘上一个 $- 1$ 的系数，对于一种方案来说，它实际上对答案的贡献（加到答案上的值是） $1)^k$ ，其中 $k$ 表示这种方案中有多少邻居不合法。

然后我们考虑现在的所有位置，存在着两种情况，一种叫做“非法”，一种叫做“不管”，这些东西形成了一些连续段，最终拼成了整个序列。

那么可以将数列拆成 $1$ 个不知道+ $x\geq 0$ 个非法的若干连续段，相当于编出来一个转移。

那么就可以根据这个东西把序列划分为若干个阶段，然后设出状态。即 $f_i$ 表示以 $i$ 为结尾的所有容斥系数之和。容易发现 $f_i$ 等于长度为 $i$ 的合法序列的数量。

那么就会有 $f_i=\underset{j\geq 0}{\sum}f_{i-j}\cdot w_{j}\cdot h(j)$ ，相当于枚举最后一个非法段的长度。
那么 $h(j)=(-1)^{j-1}$ ，因为长度为 $j$ 的非法段其实指定了 $j - 1$ 个非法位置，以及开头有一个不管的位置。

$w_j$ 表示长度为 $j$ 的非法段共有多少种，容易发现这种段的长度为 $\log m$

这样可以做到 $O((n+m)\log m)$

$n\leq 10^{18},m\leq 10^6$ ：
转移与前面 $\log m$ 项有关，可以矩阵加速。
$O(\log^3m\log n+m \;\text{poly}\log m)$

$n\leq 10^{18},m\leq 10^9$ ：配合各类筛法以及根号分治。

AT_dp_y/CF599C

不能走黑不好做。考虑容斥，设 $S_i$ 表示第 $i$ 个黑色格子不走的方案数，则 $ans=|\bigcap S_i|$ ，其补集转化为走一些黑色格子。

设 $f (x)$ 表示选出 $x$ 个黑走的方案数，则 $ans=\underset{i=0}{\overset n\sum}(-1)^if(i)$

我们先把黑色格子以 $(x, y)$ 升序排列，然后设 $f_i$ 表示必然走第 $i$ 个黑格子的所有方案的系数和，在这里会发现这实际上相当于以第 $i$ 个黑格子为终点，其他黑色格子不走的方案数。

那么转移就是 $f_i=\underset{j<i}{\sum}-\begin{pmatrix}x_i-x_j+y_i-y_j\\x_i-x_j\end{pmatrix}f_j$ ，表示枚举之前走了哪个黑色格子。
这里的 $- 1$ 是因为当前走了一个黑色格子，所以要乘上 $- 1$ 的系数。
组合数是表示从上一个黑色格子走到这里的方案数。

这样会发现一个问题是，这样没有办法表示是从左上角出发，到右下角结束的。因此我们强制在左上角和右下角添加一个黑色格子。并且令初值 $f_1=-1$ ，表示走了左上角黑色格子的方案容斥系数和。

观察转移的形式，我们会发现 $f_i$ 实际上表示的是走了左上角那个黑色格子，以及第 $i$ 个黑色格子的方案数，这样就可以做了。

时间复杂度 $O(n^2)$

CF1728G

标算做法是由于每次只添加一盏灯，因此会照亮一个连续段，只需要剩下的灯照亮前后缀即可，预处理前后缀就能算出来。

但是有多项式做法。

考虑容斥是怎么做的，相当于选出一些点强制不能照亮，剩下点随意，这样方案数是好求的。
那么对于一种照亮的情况，我们可以把它划分为首尾不能照亮+中间随意的连续段，那么设 $f_i$ 表示第 $i$ 个点为结尾的容斥系数和，转移相当于枚举最后一个左右为不能照亮，中间是任意的连续段。（以 $i$ 为结尾，说明 $i$ 不能照亮）

那么 $f_i=\underset{j<i}\sum- w_{j,i}\cdot f_j$

$w$ 是 $O(nm^2)$ 好算的。

这样dp出来相当于强制第一个点和第 $i$ 个点不能照亮的方案数，所以我们在正负无穷的位置添加两个点，就可以dp出答案。

这样每次询问 $w$ 只会有 $m^2$ 个位置（在这次询问中）改变。

复杂度为 $O((n+q)m^2)$

填数（模拟赛题）

给定 $n, m, k$ 和 $k$ 个区间 $l_i,r_i)$ ，求有多少个长为 $n$ 的正整数数组 $a$ 满足：

$\leq a_i \leq m$ 。
对于每个给定的区间 $l_i,r_i)$ ，存在至少一对 $l_i \leq p_0 < p_1 \leq r_i$ ，满足 $a_{p_0} = a_{p_1}$ 。

答案对 $10^9 + 7$ 取模。 $\leq n,m \leq 10^6$ ， $\leq k \leq 2000$ 。

区间问题一个经典套路是不存在相交区间或者不存在包含区间。
本题中我们发现子集严格强于超集，因此不存在包含区间。我们把包含区间去重之后编一个后效性消除，把区间按照右端点升序排列。

然后我们把 $=$ 容斥为 $\not=$ ，相当于强制一些区间当中没有重复的数字，然后用dp的方法把容斥系数乘起来。

设 $f_i$ 表示考虑前 $i$ 个区间，第 $i$ 个区间被选为非法的所有情况的容斥系数和，则：

$f_i=\underset{j<i}\sum -f_j\cdot \left\{\begin{matrix} l_i>r_j:m^{\underline{len_i}}\cdot m^{l_i-r_j}\hspace{2.25cm}\\ else:(m-(r_j-l_i+1))^{\underline{len_i-(r_j-l_i+1)}} \end{matrix}\right.$

强制开头结尾有一个区间即可。

P4099

首先这个题有不容斥的做法，如果设 $f_u$ 表示以 $u$ 为子树的答案会发现没法转移，因为不知道子树内部拓扑序的情况。
如果我们想要把一个儿子加入，必须要知道这个儿子在拓扑序列中的排名，因此必须要记录进状态里，即 $f_{u,i}$ 表示以 $u$ 为子树， $u$ 在拓扑序列中的顺序为 $i$ 的方案数。然后编一个转移就可以了。

但是这个题也可以容斥（虽然容斥做法好像更难一点…）

具体来说，一条边其实提供了一个限制，即 $u\rightarrow v$ 说明 $u$ 的拓扑序在 $v$ 之前，如果只有内向边是好做的，那我们选择对外向边容斥。
设 $S_i$ 表示满足所有内向边的限制和第 $i$ 条外向边限制的所有序列构成的集合，则答案为 $|\bigcap S_i|$ ，那么补集相当于取到一些外向边，然后把它们反转为内向边，剩下一些外向边断开的方案数。

那么如果我们指定一个反转，可以认为那条外向边带有 $- 1$ 的容斥系数。

非常容易编出来一个dp，即 $f_u$ 表示 $u$ 子树的答案，转移考虑把 $u$ 的一个儿子合并到 $u$ 子树内部，如果是内向边，就乘上 $\begin{pmatrix}siz_u+siz_v-1\\siz_v\end{pmatrix}$ 合并，表示 $u$ 为最后一个节点，前面 $siz_u+siz_v-1$ 个位置选出 $siz_v$ 个位置放置 $v$ 子树内部的拓扑序列情况。
如果是外向边，那么就考虑两种情况。
一种叫做反转，这时候带有 $-\begin{pmatrix}siz_u+siz_v-1\\siz_v\end{pmatrix}$ 的系数。
另一种叫做断开，这时候带有 $\begin{pmatrix}siz_u+siz_v\\siz_v\end{pmatrix}$ 的系数，因为与 $u$ 没有关系了， $u$ 不一定是最后一个，因此可以在任意位置插入。

void dfs(int u,int fa) {
	f[u]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		dfs(v,u);
		if(w) f[u]=f[u]*f[v]%M*C[siz[u]+siz[v]-1][siz[v]]%M;
		else f[u]=f[u]*f[v]%M*C[siz[u]+siz[v]-1][siz[v]-1]%M;
		siz[u]+=siz[v];
	}
}

但是会发现这样是错的。

具体错误是，假如说要合并一个子树，并且一种情况经过了断边/反转之后 $u$ 的连通块大小实际上为 $x$ ， $v$ 的连通块大小为 $y$ ，但是我们在合并内向边的时候强制 $u$ 在最后一个，即从 $siz_u+siz_v-1$ 中选，实际上是不对的，我们只需要强制在 $x + y$ 个位置中， $u$ 在最后一个即可。那我们可以修改一下状态，即设 $f_{u,x}$ 表示目前所在的内向连通块大小为 $x$ 的方案数，现在再来编一下转移：

内向边： $f_{u,x+y}\leftarrow +f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\x+y\end{pmatrix}\begin{pmatrix}x+y-1\\y\end{pmatrix}$ ，表示先选出拓扑序列的一些位置放连通块，然后再连通块内部安排放置顺序，在放连通块的位置内部安排顺序时，必须强制 $u$ 在最后一个位置。
外向边取反： $f_{u,x+y}\leftarrow -f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\x+y\end{pmatrix}\begin{pmatrix}x+y-1\\y\end{pmatrix}$
外向边断开： $f_{u,x}\leftarrow +f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\siz_v\end{pmatrix}$

void dfs(int u,int fa) {
	f[u][1]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		
		dfs(v,u);
		
		memset(g,0,sizeof g);
		
		for(int i=1;i<=siz[u];i++)
			for(int j=1;j<=siz[v]&&i+j<=n;j++)
				if(w)
					(g[i+j]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][i+j]%M*C[i+j-1][j]%M)%=M;
				else
					(g[i]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M,
					(g[i+j]+=(M-1)*f[u][i]%M*f[v][j]%M*C[siz[u]+siz[v]][i+j]%M*C[i+j-1][j]%M)%=M;
		
		memcpy(f[u],g,sizeof g);
		siz[u]+=siz[v];
	}
}

但是这样会发现连样例都过不了。原因是系数乘错了。乘错的原因是，在 $f_{u,x}$ 中，已经乘上了 $\begin{pmatrix}siz_u\\x\end{pmatrix}$ 作为大小为 $x$ 的连通块放在 $siz_u$ 个位置的方案，然后在转移到 $f_{u,x+y}$ 时又选了一次，这样就选多了。事实上只需要在 $siz_u+siz_v$ 个位置中选出 $siz_v$ 个位置放新子树的拓扑序信息即可。但是这样就没法限制 $v$ 在 $u$ 前了，具有后效性，而增加一维状态记录 $u$ 在拓扑序中的位置，来消除后效性在时间上是不可能的，因此我们选择推迟后效性。

转移：

内向边： $f_{u,x+y}\leftarrow +f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\siz_v\end{pmatrix}$ ，表示先选出拓扑序列的一些位置放连通块，然后再连通块内部安排放置顺序，在连通块内部安排顺序时，必须强制 $u$ 在最后一个位置。
外向边取反： $f_{u,x+y}\leftarrow -f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\siz_v\end{pmatrix}$
外向边断开： $f_{u,x}\leftarrow +f_{u,x}f_{v,y}\begin{pmatrix}siz_u+siz_v\\siz_v\end{pmatrix}$

注意是先合并再修改 $f$ ，具体看代码。

当我们把 $u$ 的所有子树合并完成之后，考虑一个实际上大小为 $x$ 的连通块，其中由于我们并没有限制 $u$ 必须要在其他节点之前，因此答案会多算 $x$ 倍，因此再除掉就可以了：
$f_{u,x}\leftarrow f_{u,x}\cdot \frac 1x$

#include<iostream>
#include<cstring>
#include<vector>
#include<map>
#include<numeric>
using namespace std;
const int N=1e3;
const long long M=1e9+7;
long long C[N+5][N+5];
long long f[N+5][N+5];
long long g[N+5];
long long siz[N+5];
long long inv[N+5];
vector<vector<pair<int,int>>>a;
int n;
void dfs(int u,int fa) {
	f[u][1]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		
		dfs(v,u);
		
		memset(g,0,sizeof g);
		
		for(int i=1;i<=siz[u];i++)
			for(int j=1;j<=siz[v]&&i+j<=n;j++)
				if(w)
					(g[i+j]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
				else {
					(g[i]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
					(g[i+j]+=(M-1)*f[u][i]%M*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
				}
		
		memcpy(f[u],g,sizeof g);
		siz[u]+=siz[v];
	}
	for(int i=1;i<=siz[u];i++)
		(f[u][i]*=inv[i])%=M;
}
int main() {
	for(int i=0;i<=N;i++) C[i][i]=C[i][0]=1;
	inv[0]=inv[1]=1;
	for(int i=2;i<=N;i++) (inv[i]=(M-1)*(M/i)%M*inv[M%i])%=M;
	for(int i=1;i<=N;i++)
		for(int j=1;j<=N;j++)
			(C[i][j]=C[i-1][j-1]+C[i-1][j])%=M;
	int T;
	cin>>T;
	while(T--) {
		memset(f,0,sizeof f);
		memset(siz,0,sizeof siz);
		a.resize(0);
		cin>>n;
		a.resize(n+5);
		for(int i=1,u,v;i<n;i++) {
			char c;
			cin>>u>>c>>v;
			u++;
			v++;
			if(c=='<') a[u].push_back({0,v}),a[v].push_back({1,u});
			else a[u].push_back({1,v}),a[v].push_back({0,u});
		}
		dfs(1,0);
		cout<<accumulate(f[1]+1,f[1]+n+1,0ll)%M<<endl;
	}
}
/*
1
4
1 < 0
2 < 0
3 < 0

1 
3
0 < 1
0 < 2

1
4 
0 < 1 
0 < 2 
0 < 3

*/

ARC101_C

树上任意一边都没覆盖，容斥为选出一些边不被覆盖，每选出这样一条边，就在这种方案上乘一个 $- 1$ 的系数。

考虑一个dp，再合并完所有子树之后，如果我们要断开它与父亲的那条边，那就要求出子树内部随意匹配的方案数，显然与子树连通块的大小有关，因此要记录一维表示子树连通块的大小。

设 $f_{u,i}$ 表示以 $u$ 为根的子树目前有大小为 $i$ 的不知道边构成的连通块的方案数，转移就是考虑把儿子 $v$ 合并进来：

$f_{u,x+y}\leftarrow+f_{u,x}f_{v,y}(x>0,y\geq 0)$

先合并再修改。

如果 $u$ 和父亲的连边是断开的，那么 $u$ 父亲边的状态是“非法”，不是“未指定”，因此不知道连通块的大小为 $0$ ，则 $f_{u,0}$ 表示断边的容斥方案数，我们dp求出 $f_{u,x>0}$ 后考虑求出 $f_{u,0}$

那么 $f_{u,0}\leftarrow-f_{u,i}w_i$ ，表示我们指定它向父亲的连边是断开的，因此带有 $- 1$ 的系数。
$w_i$ 表示大小为 $i$ 的连通块任意匹配方案数，显然 $w_{奇数}=0$ ，现在考虑偶数是如何递推的。

我们想要从 $w_{i-2}$ 递推到 $w_i$ ，那么就需要增加一对匹配，可以选择新增一对匹配，这样方案数是 $1$ ，或者选择新增两个点，然后断开原来的 $\frac {i-2}2$ 组中的一组匹配，新的两个点和旧的两个点形成两组匹配，这样配对会有 $2$ 种方案，这样方案数是 $2\left(\frac{i-2}2\right)=i-2$

因此 $w_i=(1+i-2)w_{i-2}=(i-1)w_{i-2}$

或者得到 $w_i=\underset{j=1}{\overset {j/2}\prod}(2j-1)$ ，表示每次选出最小的点进行匹配。
初值为 $f_{u,1}=1$ ，答案为 $f_{1,0}$ ，因为转移的时候假设根节点连向父亲的边断开了，所以乘了一个 $- 1$ 的系数，要再乘回来。

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int N=5e3;
const long long M=1e9+7;
vector<int> a[N+5];
long long w[N+5];//i对
long long f[N+5][N+5];
int siz[N+5];
int n;
long long g[N+5];
void dfs(int u,int fa) {
	siz[u]=1;
	for(auto&v:a[u])
		if(v^fa) {
			dfs(v,u);
			memset(g,0,sizeof g);
			for(int x=1; x<=siz[u]; x++)
				for(int y=0; y<=siz[v]; y++)
					if(x+y<=N)
						(g[x+y]+=f[u][x]*f[v][y])%=M;
			memcpy(f[u],g,sizeof f[u]);
			siz[u]+=siz[v];
		}
	for(int i=0; i<=n; i++)
		(f[u][0]+=(M-1)*f[u][i]%M*w[i]%M)%=M;
}
int main() {
	cin>>n;
	for(int i=1,u,v; i<n; i++) {
		cin>>u>>v;
		a[v].push_back(u);
		a[u].push_back(v);
	}
	w[0]=1;
	for(int i=2; i<=n; i+=2) w[i]=w[i-2]*(i-1)%M;

	for(int i=1; i<=n; i++) f[i][1]=1;
	dfs(1,0);

//	for(int i=1;i<=n;i++,cout<<endl)
//		for(int j=0;j<=n;j++,cout<<' ')
//			cout<<f[i][j];
	cout<<(M-1)*f[1][0]%M;
}

话说不知道为啥初值设为 $- 1$ 也能过，有人知道请您联系我。

有标号连通图计数

求 $n$ 个节点的无向连通图有多少个，节点有标号，编号为 $[1, n]$
$n <= 5000$

这个题是朴素容斥，即考虑如何用容斥原理来修正答案。

设 $f_i$ 表示大小为 $i$ 的连通图数量，一个想法是首先连出一棵树，但是不太好搞，考虑补集转换，总边数为 $\frac{i(i-1)}2$ ，总可能性为 $h(i)=2^{\frac {i(i-1)}2}$ 种，减去不连通的情况即可，那我们枚举 $1$ 号点所在的连通块大小 $j$ ，然后从剩下的 $i - 1$ 个点中选出 $j - 1$ 个点，情况数量为： $f_j \begin{pmatrix}i-1\\ j-1\end{pmatrix}$ ，剩下 $i - j$ 个点随意连边，转移方程为：
$f_i=h(i)-\underset{j<i}\sum f_j \begin{pmatrix}i-1\\ j-1\end{pmatrix}h(i-j)$

山东省队集训

给定一张 $n\leq 15$ 个点 $m\leq 200$ 条边的无向图，对于所有 $k$ ，请求出保留恰好 $k$ 条边使得整张图连通的方案数。

容斥，设 $f_{i,S}$ 表示保留了 $i$ 条边，使得 $S$ 连通的方案数。不连通就枚举 $1$ 所在的连通块。
$f_{i,S}=\begin{pmatrix}cnt_S\\i\end{pmatrix}-\underset{1\in T\subsetneq S}{\sum}\underset{j=0}{\overset i\sum}f_{j,T}\begin{pmatrix}cnt_{S-T}\\i-j\end{pmatrix}$

$cnt_S$ 表示两端都在 $S$ 内的边的数量，时间复杂度 $O(3^nm^2)$ ，难以通过。

观察到转移系数只与 $cnt_{S-T}$ 有关，把 $c n t$ 相同的 $T$ 一起转移，复杂度 $O(3^nm+2^nm^3)$ ，可以通过：
$f_{i,S}=\begin{pmatrix}cnt_S\\i\end{pmatrix}-\underset{k=0}{\overset i\sum}\underset{j=0}{\overset i\sum}\begin{pmatrix}k\\i-j\end{pmatrix}\times g_j(S,k)$

其中 $g_i(S,k)=\underset{1\in T\subsetneq S}\sum[cnt_{S-T}=k]f_{i,T}$

我们枚举一个 $S, T, i$ ，把它贡献到对应的 $g$ 上即可。

或者把 $f_i$ 看成多项式的形式，那么就是 $1+x)^?$ 的形式，那我们令 $(1 + x) = y$ ，转移就变成了多项式平移，可以 $O (m)$ 完成。

或者还有一种我没看懂的做法：
（来自lyp的PPT）
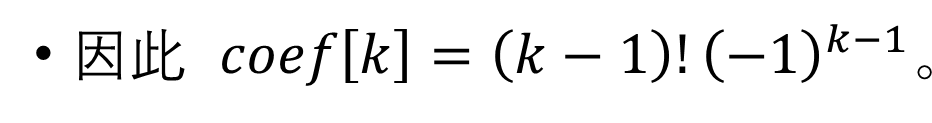
在这里插入图片描述

没有看懂，如果您看懂了的话，请您联系我。

LOJ575

首先想到的是离散dp。
考虑如果我们要往序列后面添加一个数字，那么我们只需要知道原来的序列末尾在序列中的排名，就可以知道我们能添加多少个比它小/大的数字了。

设 $f_{i,j}$ 表示长度为 $i$ 的序列值域为 $[1, i]$ ，末尾为 $j$ 的方案数，如果是小于号，那么 $f_{i,j}(n-j+1)+\rightarrow f_{i+1,k>j}$ ，表示我们向 $[1, i]$ 中插入一个比 $j$ 大的数字 $k$ ，把值域变为 $[1, i + 1]$ ，大于号同理。

但是这样 $O(n^2)$ 到顶了。

考虑容斥，我们对大于号容斥，那么一些大于号会变成小于号，另一些会变成不知道。
那么符号序列就可以拼成一个不知道+若干个非法。

$f_i$ 表示dp到了第 $i$ 个数字的系数和，转移就是枚举最后一个上升序列是 $(j, i]$ ，同时要求 $a_j=‘>’$ ，表示 $a_j$ 被我们容斥为了不知道：
$f_i=\underset{j<i}\sum [a_j=‘>’](-1)^{cnt_{i-1}-cnt_j}f_j\begin{pmatrix}i\\j\end{pmatrix}$

时间复杂度 $O(n^2)$

做分治NTT即可优化到 $O(n\log^2n)$

ABC236Ex

如果到图上考虑，相等连边，那么合法方案数就是图全部不连通的方案数。

设 $S_i$ 表示第 $i$ 条边不存在的方案集，则要求的就是 $|\bigcap S_i|$ ，补集就是指定一些边存在，另一些边不知道。

那么可以对边集容斥，就获得了 $O\left(2^{\frac{n(n-1)}2}\right)$ 的做法。

相当于我们把点集 $[n]$ 划分为若干集合 ${S_1,S_2,S_3,...,S_k\}$ ，确保内部连通，外部不知道。

设 $f_S$ 表示考虑 $S$ 内部的容斥系数之和。转移就是枚举最后一个被选出的连通块。
$f_S=\underset{u\in T\subseteq S}\sum w_{T}\cdot h'(T)\cdot f_{S-T}$

那我们只需要知道 $h^{'} (T) = h (∣ T ∣)$ 即可，那就是使得 $∣ T ∣$ 个点的图连通的所有方案的容斥系数之和。

可以通过一个打表小容斥求出：
$n$ 个点的所有方案的容斥系数和为，枚举实际上选了几条边，得到：
$H(n)=\underset{i=0}{\overset{\frac{n(n-1)}2}\sum}\begin{pmatrix}\frac{n(n-1)}2\\i\end{pmatrix}(-1)^i=[n=1]$

那么它等于连通+不连通的系数和，如果不连通，那么枚举1所在的连通块大小：
$H(n)=h(n)+\underset{i=1}{\overset {n-1}\sum}\begin{pmatrix}n-1\\i-1\end{pmatrix}h(i)H(n-i)=h(n)+\underset{i=1}{\overset {n-1}\sum}\begin{pmatrix}n-1\\i-1\end{pmatrix}h(i)[n-1=i]$