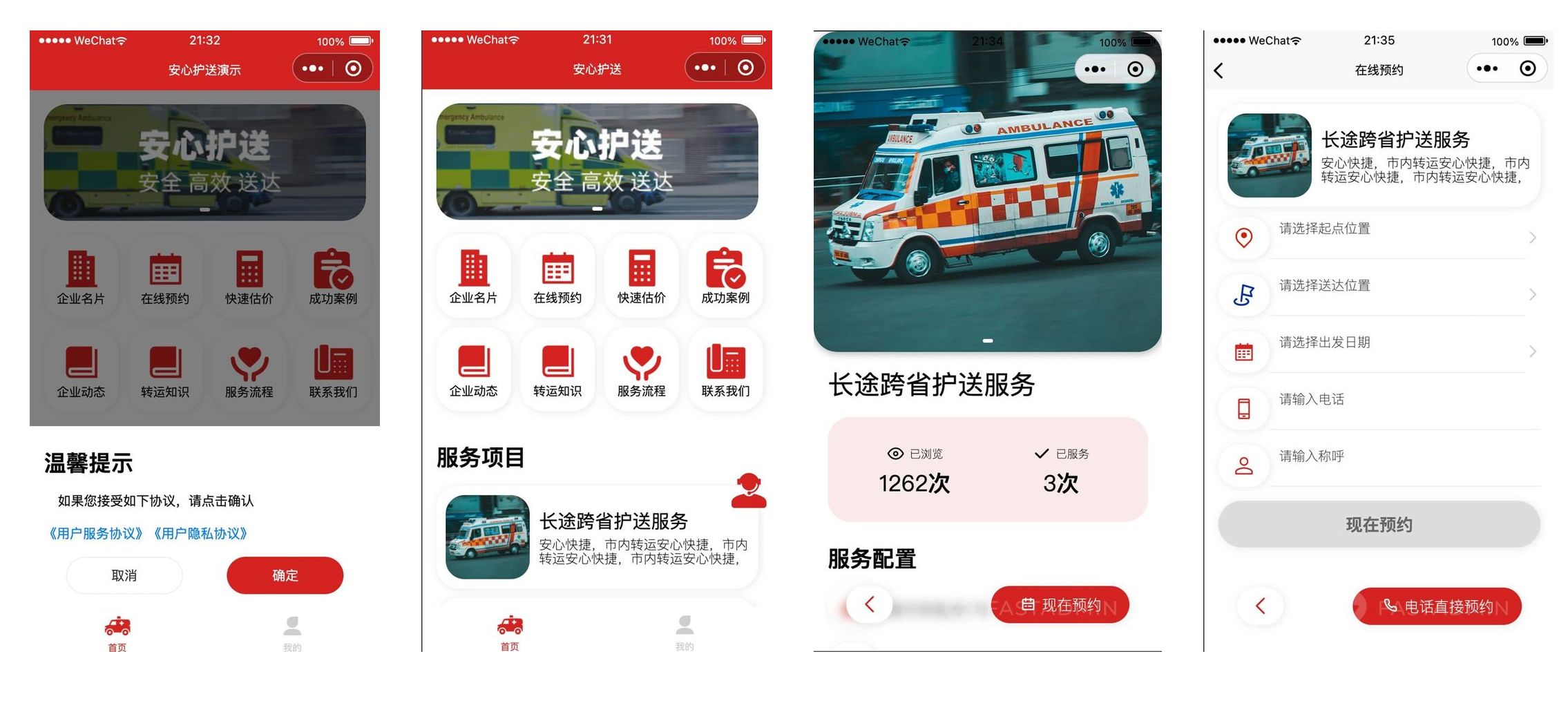
牛顿二项公式

$$(x+y{)}^n=\stackrel{n}{\sum _{k=0}}{C}_n^k\cdot x^{n-k}{y}^k$$.

映射

$f:X\to Y$，$f$ 为 $X$ 到 $Y$ 的映射。$f$ 是一个对应关系，$X,Y$ 是两个非空集合。在对应关系 $f$ 下，$X$ 中的元素 $x$ 在 $Y$ 中有唯一确定的元素 $y$ 与之对应。

• $y$ 为 $x$ 在 $f$ 下的像。
• $x$ 为 $y$ 在 $f$ 下的原像。

集合 $X$ 是 映射 $f$ 的定义域，记 $D_f$，即 $D_f=X$.

$X$ 中所有元素的 像 组成的 集合 称为 映射$f$ 的 值域，记 $R_f$ 或 $f(X)$，即 R f = f ( X ) = { f ( x ) ∣ x ∈ X } R_f=f(X)=\{f(x)|x\in X\} Rf​=f(X)={f(x)∣x∈X}.

• 对于每一个元素 $x\in X$，在 $Y$ 中的像 $y$ 是唯一的。但对于每一个元素 $y\in Y$，在 $X$ 中的原像不一定是唯一的。
• $R_f\subset Y$，不一定 $R_f=Y$.

---

对于 $f:X\to Y$，

• 若 $R_f=Y$，则称 $f:X\to Y$ 为 满射。（集合 $Y$ 中每个元素在集合 $X$ 中都能找到它的原像。）
• 若 $x_1\ne x_2,(x_1,x_2\in X)$ 且 $f(x_1)\ne f(x_2)$，则称 $f:X\to Y$ 为 单射。（集合 $X$ 中任意两个元素在 $Y$ 中的像不相等，$X$ 中任意两个元素的像没有重复。）
• 既是满射又是单射的映射称为一一映射或双射。

---

映射又称算子。在不同数学分支有着不同的惯用名，非空集 $X$ 到 数集 $Y$ 的映射称为 $X$ 上的 泛函；从非空集 $X$ 到它自身的映射又称为 $X$ 上的 变换；从 实数集 $R$（或其子集） 到实数集 $Y$ 的映射通常称为 定义在 $X$ 上的 函数。

---

逆映射与复合映射：

$f:X\to Y$ 是单射，则其存在逆映射。

$f:X\to Y$ 是单射，则 $y\in R_f$，有唯一的 $x\in X$，$f(x)=y$.

定义一个新的映射 $g:R_f\to X$，每个 $y\in R_f$，$g(y)=x$.

$g$ 为 $f$ 的 逆映射。记 $g=f^{-1}$，$g$ 的定义域 $Dg=D_{f^{-1}}=R_f$，$g$ 的值域 $R_g=R_{f^{-1}}=X$.

---

$f:[-\frac{\pi }{2},\frac{\pi }{2}]\to [-1,1]$，对每个 $x\in [-\frac{\pi }{2},\frac{\pi }{2}]$，$f(x)=\sin x$ 是一个映射，定义域 $D_f=[-\frac{\pi }{2},\frac{\pi }{2}]$，值域 $R_f=[-1,1]$. 此时，$f$ 是一个单射，所以其存在逆映射 $f^{-1}=\arcsin x,x\in [-1,1]$，$f^{-1}$ 就是反正弦函数，定义域 $D_{f^{-1}}=[-1,1]$，值域 $R_{f^{-1}}=[-\frac{\pi }{2},\frac{\pi }{2}]$.

---

两个映射 $g:X\to Y_1$ 和 $f:Y_2\to Z$，

$Y_1\subset Y_2$，则可以定义复合映射：

$f\circ g:X\to Z,(f\circ g)(x)=f[g(x)],x\in X$.

• 满足条件：$R_g\subset D_f$.
• $f\circ g$ 有意义并不代表 $g\circ f$ 有意义.
• $f\circ g$ 和 $g\circ f$ 都有意义，符合映射 $f\circ g$ 与 $g\circ f$ 也未必相同.

---

映射 $g:\mathrm{R}\to [-1,1]$，对每个 $x\in \mathrm{R}$，$g(x)=\sin x$；映射 $f:[-1,1]\to [0,1]$，对每个 $u\in [-1,1]$，$f(u)=\sqrt{1-u^2}$，

复合映射 $f\circ g:\mathrm{R}\to [0,1]$，对每个 $x\in \mathrm{R}$，有 $(f\circ g)(x)=f[g(x)]=f(\sin x)=\sqrt{1-{\sin }^{2}x}=|\cos x|$.

---

函数

定义：设数集 $D\subset \mathrm{R}$，则称映射 $f:D\to \mathrm{R}$ 为定义在 $D$ 上的函数，通常记为 $y=f(x),x\in D$。

• $x$ 自变量
• $y$ 因变量
• $D$ 定义域，记 $D_f$.

$x$ 处的函数值 $y=f(x)$. $x$ 与 $y$ 的函数关系。全体函数值 $f(x)$ 构成的集合称为值域 $R_f$ 或 $f(D)$. R f = f ( D ) = { y ∣ y = f ( x ) , x ∈ D } R_f=f(D)=\{y|y=f(x),x\in D\} Rf​=f(D)={y∣y=f(x),x∈D}.

---

符号函数：$y=\mathrm{sgn}x=\{\begin{array}{ll}-1,& x<0,\\ 0,& x=0,\\ 1,& x>0.\end{array}$

$x=\mathrm{sgn}x\cdot x$.

---

取整函数：$y=[x]$，图像为阶梯曲线，定义域 $D=(-\infty ,+\infty )$，值域 $R_f=\mathrm{Z}$.

---

函数的特性

• 有界性：
  • $f(x)\le K_1$，$K_1$ 为 $f(x)$ 在 $X$ 上的一个 上界
  • $f(x)\ge K_2$，$K_2$ 为 $f(x)$ 在 $X$ 上的一个 下界
  • $|f(x)|\le M$，$f(x)$ 在 $X$ 上 有界
  • $\forall M\in {\mathrm{R}}^{+},\exists x_1\in X,|f(x_1)|>M$，则 $f(x)$ 在 $X$ 上无界。
  • 若 $f(x)$ 在 $X$ 上既有上界又有下届，则 $f(x)$ 在 $X$ 上有界。
• 单调性：
  • $f(x)$，$I\subset D$，$\forall x_1,x_2\in I,x_1<x_2$，有 $f(x_1)<f(x_2)$，则 $f(x)$ 在区间 $I$ 上是 单调增加 的。
  • $f(x)$，$I\subset D$，$\forall x_1,x_2\in I,x_1<x_2$，有 $f(x_1)>f(x_2)$，则 $f(x)$ 在区间 $I$ 上是 单调减少 的。
  • 单调增加和单调减少的函数统称为 单调函数。

---

函数的奇偶性：

• $f(x)=f(-x)$，关于 $x=0$ 对称，偶函数。
• $f(x)=-f(-x)$，关于 $(0,0)$ 对称，奇函数。

---

函数的周期性：

$f(x)$ 定义域 $D$，$\exists l\in {\mathrm{R}}^{+}$，使 $\forall x\in D$ 有 $(x\pm l)\in D$，且 $f(x+l)=f(x)$. 则称 $f(x)$ 为周期函数，$l$ 称为 $f(x)$ 的周期，（最小正周期）。

---

$y=\sin x$ ：(奇函数，周期 $2\pi$.)

---

$y=\cos x$ ：(偶函数，周期 $2\pi$.)

---

$y=\sin (x+\frac{\pi }{4})$：

---

$y=\sin x+\cos x$ ：(非奇非偶函数，周期 $2\pi$.)

$y=\sin x+\cos x=\sqrt{2}(\sin x\cdot \frac{\sqrt{2}}{2}+\cos x\cdot \frac{\sqrt{2}}{2})$

$=\sqrt{2}(\sin x\cdot \cos \frac{\pi }{4}+\cos x\cdot \sin \frac{\pi }{4})$

$=\sqrt{2}\sin (x+\frac{\pi }{4})$.

$y=\sqrt{2}\sin (x+\frac{\pi }{4})$ 由 $y=\sin x$ 左移了 $\frac{\pi }{4}$ 单位再整体乘以 $\sqrt{2}$ 得来。

---

$y=\tan x$ ：(奇函数，周期 $\pi$.)

---

Dirichlet 狄利克雷函数：

$D(x)=\{\begin{array}{ll}1,& x\in \mathrm{Q},\\ 0,& x\in {\mathrm{Q}}^C.\end{array}$

${\mathrm{Q}}^C$，角标 $C$ 一般表示有理数集 $\mathrm{Q}$ 相对于实数集 $\mathrm{R}$ 的补集，${\mathrm{Q}}^C$ 的意思就是 无理数集。

任何有理数加上一个有理数，还是有理数；任何无理数加上一个有理数，还是一个无理数。对于这个函数，任何有理数都是它的周期。

$\because$ 没有最小的有理数

$\therefore$ Dirichlet 函数没有最小正周期。

---

反函数与复合函数

反：

设函数 $f:D\to f(D)$ 是单射，则它存在逆映射 $f^{-1}:f(D)\to D$，则称此映射 $f^{-1}$ 为函数 $f$ 的反函数。

一般地，$y=f(x)$，$x\in D$ 的反函数记成 $y=f^{-1}(x),x\in f(D)$.

相对于反函数 $y=f^{-1}(x)$ 来说，原来的函数 $y=f(x)$ 称为 直接函数，它俩在函数图像上关于直线 $y=x$ 对称，其实 $y=f^{-1}(x)$ 就是由 $y=f(x)$ 对换 $x$ 轴 和 $y$ 轴 得到的函数图像。

复合：

$y=f(u)$ 定义域 $D_f$，$u=g(x)$ 定义域 $D_g$，其值域 $R_g\subset D_f$，则确定一个 复合函数 : $y=f[g(x)],x\in D_g$. $u$ 为 中间变量。

先 $g$ 后 $f$ 的复合，记为 $f\circ g$，即：$(f\circ g)(x)=f[g(x)]$.

---

$f(x),g(x)$ 的定义域为 $D_f,D_g$，$D=D_f\cap D_g\ne \varnothing$，定义两个函数的运算：

• 和（差）：$(f\pm g)(x)=f(x)\pm g(x),x\in D;$
• 积： $(f\cdot g)(x)=f(x)\cdot g(x),x\in D;$
• 商： ( f g ) ( x ) = f ( x ) g ( x ) , x ∈ D − { x ∣ g ( x ) = 0 , x ∈ D } \Big(\dfrac{f}{g}\Big)(x)=\dfrac{f(x)}{g(x)},\quad x\in D-\{x|g(x)=0,x\in D\} (gf​)(x)=g(x)f(x)​,x∈D−{x∣g(x)=0,x∈D}.

---

任何定义在 $(-l,l)$ 上的函数 $f(x)$ 都可以写成 $f(x)=g(x)+h(x)$ 的形式，其中 $g(x)$ 为 $(-l,l)$ 上的偶函数，$h(x)$ 为 $(-l,l)$ 上的奇函数。

设函数 $f(x)$ 的定义域为 $(-l,l)$，证明必存在 $(-l,l)$ 上的偶函数 $g(x)$ 及奇函数 $h(x)$，使得 $f(x)=g(x)+h(x)$.

证明：

假设存在这种的 $g(x)$ 和 $h(x)$，使得 $f(x)=g(x)+h(x)$.

且 $g(x)=g(-x)$，$h(-x)=-h(x)$.

则 $f(-x)=g(-x)+h(-x)=g(x)-h(x)$.

$g(x)=\frac{1}{2}[f(x)+f(-x)]$.

$h(x)=\frac{1}{2}[f(x)-f(-x)]$.

$g(x)+h(x)=f(x)$.

$g(-x)=\frac{1}{2}[f(-x)+f(x)]=g(x)$.

$h(-x)=\frac{1}{2}[f(-x)-f(x)]=-h(x)$.

由结论 $f(x)=g(x)+h(x)$ 反推条件 $g(x)=g(-x)$，$h(-x)=-h(x)$.

当 $f(x)$ 是偶函数时，$h(x)=0$，它既是关于 $x=0$ 对称的偶函数，也是关于 $(0,0)$ 对称的奇函数。

初等函数

• 幂函数：$y=x^{\mu }$，（$\mu \in \mathrm{R}$ 是常数）
• 指数函数：$y=a^x$，（$a>0$，$a\ne 1$）
• 对数函数：$y={\log }_{a}x$，（$a>0$ 且 $a\ne 1$，特别当 $a=e$ 时，记为 $y=\ln x$，$e\approx 2.718$，是一个无理数。）
• 三角函数：$y=\sin x,y=\cos x,y=\tan x$ 等
• 反三角函数：$y=\arcsin x,y=\arccos x,y=\arctan x$ 等

以上这五类为 基本初等函数。

由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数，称为初等函数，例如：

$y=\sqrt{1-x^2},y={\sin }^{2}x,y=\sqrt{\cot \frac{x}{2}}$

---

双曲正弦

$y=\mathrm{sh}x=\frac{e^x-e^{-x}}{2}$

双曲余弦

$y=\mathrm{ch}x=\frac{e^x+e^{-x}}{x}$

双曲正切

$y=\mathrm{th}x=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

公式

• $\mathrm{sh}(x\pm y)=\mathrm{sh}x\cdot \mathrm{ch}y\pm \mathrm{ch}x\cdot \mathrm{sh}y$
• $\mathrm{ch}(x\pm y)=\mathrm{ch}x\cdot \mathrm{ch}y\pm \mathrm{sh}x\cdot \mathrm{sh}y$

对于 $\mathrm{ch}(x-y)=\mathrm{ch}x\cdot \mathrm{ch}y-\mathrm{sh}x\cdot \mathrm{sh}y$，当 $x=y$ 时，有 $\mathrm{ch}(x-x)=\mathrm{ch}0={\mathrm{ch}}^{2}x-{\mathrm{sh}}^{2}x=1$.

对于 $\mathrm{sh}(x+y)=\mathrm{sh}x\cdot \mathrm{ch}y+\mathrm{ch}x\cdot \mathrm{sh}y$，当 $x=y$ 时，有 $\mathrm{sh}2x=2\mathrm{ch}x\cdot \mathrm{sh}x$.

对于 $\mathrm{ch}(x+y)=\mathrm{ch}x\cdot \mathrm{ch}y+\mathrm{sh}x\cdot \mathrm{sh}y$，当 $x=y$ 时，有 $\mathrm{ch}2x={\mathrm{ch}}^{2}x+{\mathrm{sh}}^{2}x$.

双曲函数 $y=\mathrm{sh}x,y=\mathrm{ch}x(x\ge 0),y=\mathrm{th}x$ 的反函数依次记为：

反双曲正弦：$y=\mathrm{arsh}x$

反双曲余弦：$y=\mathrm{arch}x$

反双曲正切：$y=\mathrm{arth}x$

---

$y=\mathrm{sh}x$ 的反函数：$y=\mathrm{arsh}x=\ln (x+\sqrt{x^2+1})$. 推导过程如下：

$x=\mathrm{sh}y=\frac{e^y-e^{-y}}{2}$

令 $u=e^y$

$x=\frac{u-\frac{1}{u}}{2}$

$u^2-2xu-1=0$

$u=\frac{2x\pm \sqrt{4x^2+4}}{2}=x\pm \sqrt{x^2+1}$

$\because u=e^y>0$

又 $\because \sqrt{x^2+1}>x$

$\therefore$ 只能取正号：$u=x+\sqrt{x^2+1}$

$y=\mathrm{arsh}x=\ln (x+\sqrt{x^2+1})$，$x+\sqrt{x^2+1}>0$，即 $x\in (-\infty ,+\infty )$.

$-y=-f(x)=-\ln (x+\sqrt{x^2+1})=\ln \frac{1}{x+\sqrt{x^2+1}}=\ln \frac{-x+\sqrt{x^2+1}}{(\sqrt{x^2+1}+x)(\sqrt{x^2+1}-x)}=\ln \frac{-x+\sqrt{x^2+1}}{(x^2+1)-x^2}=\ln (-x+\sqrt{x^2+1})$

$=f(-x)=\ln (-x+\sqrt{x^2+1})$

$\therefore$ $y=\mathrm{arsh}x$ 是奇函数。

---

$y=\mathrm{ch}x$ 的反函数 $y=\mathrm{arch}x=\ln (x+\sqrt{x^2-1}),x\ge 1$.

定义域：当 $x<0$ 时，$x+\sqrt{x^2-1}$ 始终小于零，所以 $x$ 不能小于零；

当 $x>0$ 时，只要满足 $\sqrt{x^2-1}$ 根号下大于零即可，即 $x\ge 1$.

所以定义域为 $[1,+\infty )$. 推导过程如下：

$x=\mathrm{ch}y,y\ge 0$.

$x=\frac{e^y+e^{-y}}{2},y\ge 0$.

令 $u=e^y$

$x=\frac{u+\frac{1}{u}}{2}$

$u^2-2xu+1=0$

$u=\frac{2x\pm \sqrt{4x^2-4}}{2}=x\pm \sqrt{x^2-1}>0$

$x>0$ 且 $x^2-1\ge 0$，$\therefore x\ge 1$.

$\because u=e^y>0,y\ge 0,u\ge 1$

$\therefore$ 取正号 $u=x+\sqrt{x^2-1}$.

$\therefore y=\mathrm{arch}x=\ln (x+\sqrt{x^2-1}),x\ge 1$.

$y=\mathrm{ch}x,(x\ge 0)$ 的反函数 $y=\mathrm{arch}x$ 即反双曲余弦函数的图像：

$y=\mathrm{ch}x,(x\le 0)$ 的反函数 $y=\mathrm{arch}x$ 即反双曲余弦函数的图像：

---

$y=\mathrm{th}x=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ 的反函数 $y=\mathrm{arth}x=\frac{1}{2}\ln \frac{1+x}{1-x},x\in (-1,1)$. 下面是推导过程：

$x=\frac{e^y-e^{-y}}{e^y+e^{-y}}$

令 $u=e^y$

$x=\frac{u-\frac{1}{u}}{u+\frac{1}{u}}$，$\because u=e^y>0$，分子分母同时乘以 $u$ ：

$u=\frac{u^2-1}{u^2+1}$

$u^2-1=u^{2}x+x$

$(x-1)u^2=-x-1$

$u^2=\frac{x+1}{1-x}$

$u=\sqrt{\frac{1+x}{1-x}}$

$u=e^y=\sqrt{\frac{1+x}{1-x}}$

$y=\ln (\frac{1+x}{1-x}{)}^{\frac{1}{2}}=\frac{1}{2}\ln \frac{1+x}{1-x}$

$\frac{1+x}{1-x}>0$

$x\ne 1$

当 $x<1$ 时，$1+x>0$ 得：$x>-1$

当 $x>1$ 时，$1+x<0$ 得：$x<-1$，不成立。

所以定义域为 $(-1,1)$.

---

$y=\sec x=\frac{1}{\cos x}$，$\cos x\ne 0$，$x\ne 2k\pi \pm \frac{\pi }{2},k\in \mathrm{Z}$.

$y=\csc x=\frac{1}{\sin x}$，$\sin x\ne 0$，$x\ne k\pi ,k\in \mathrm{Z}$.

$y=\cot x=\frac{\cos x}{\sin x}=\frac{1}{\tan x}$，$\tan x\ne 0$，$x\ne k\pi ,k\in \mathrm{Z}$.

导数

什么是导数：

设函数 $y=f(x)$ 在点 $x_0$ 的某个 邻域${}^{\ast }$ 内有定义，$x$ 在 $x_0$ 处取得增量 $\Delta x$ (这个增量 $\Delta x$ 可能为正也可能为负，确切地说就是一个变化量，有正负)，点 $x_0+\Delta x$ 仍在该邻域内，相应地，因变量取得增量 $\Delta y$ ，$\Delta y=f(x_0+\Delta x)-f(x_0)$；如果 $\Delta y$ 与 $\Delta x$ 之比当 $\Delta x\to 0$ 时的极限存在，那么称函数 $y=f(x)$ 在点 $x_0$ 处可导，并称这个极限为函数 $y=f(x)$ 在点 $x_0$ 处的导数，记为 $f^{\prime }(x_0)$.

$f^{\prime }(x_0)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$.

也可记作 $y^{\prime }{|}_{x=x_0},\frac{\mathrm{d}y}{\mathrm{d}x}{|}_{x=x_0},\frac{\mathrm{d}f(x)}{\mathrm{d}x}{|}_{x=x_0}$.

---

邻域${}^{\ast }$：以 $x_0$ 为中心的任何开区间称为点 $x_0$ 的邻域，记作 $U(x_0)$；在 $U(x_0)$ 中去掉中心 $x_0$ 后，称为点 $x_0$ 的去心邻域，记作 $\stackrel{\circ }{U}(x_0)$.

设 $x_0\in \mathrm{R},\delta >0$，开区间 $(x_0-\delta ,x_0+\delta )$ 称为点 $x_0$ 的 $\delta$ 邻域，记作 $U(x_0,\delta )$. 点 $x_0$ 的去心 $\delta$ 邻域记作 $\stackrel{\circ }{U}(x_0,\delta )$，$\delta$ 称为邻域半径.

对于 $0\le |x-x_0|<\delta$ ，绝对值的几何意义为距离，$|x-x_0|$ 即 $x$ 到 $x_0$ 的距离. $0\le |x-x_0|<\delta$ 即 $x$ 到 $x_0$ 的距离大于等于 0 小于等于 $\delta$ ，$x\in (x_0-\delta ,x_0+\delta )$，即 $x\in U(x_0,\delta )$.

同样地，对于 $0<|x-x_0|<\delta$ ，意思是 $x\in (x_0-\delta ,x_0)\cup (x_0,x_0+\delta )$，即 $x\in \stackrel{\circ }{U}(x_0,\delta )$.

---

导数的本质：

从导数的定义可以看出，导数的本质就是一个求极限的运算，从函数图像上来看，导数的几何意义就是函数曲线上某点处的斜率。

---

基本导数公式

$$(\mathrm{C}{)}^{\prime }=0,(\mathrm{C}是常数).$$

$$(\sin x{)}^{\prime }=\cos x$$

$$(x^u{)}^{\prime }=u\cdot x^{u-1}$$

$$(\cos x{)}^{\prime }=-\sin x$$

$$(\tan x{)}^{\prime }=(\frac{\sin x}{\cos x}{)}^{\prime }=\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}={\sec }^{2}x$$

$$(\cot x{)}^{\prime }=(\frac{\cos x}{\sin x}{)}^{\prime }=\frac{-{\sin }^{2}x-{\cos }^{2}x}{{\sin }^{2}x}=-{\csc }^{2}x$$

$$(\sec x{)}^{\prime }=(\frac{1}{\cos x}{)}^{\prime }=-{\cos }^{-2}x\cdot (-\sin x)=\sec x\cdot \tan x$$

$$(\csc x{)}^{\prime }=(\frac{1}{\sin x}{)}^{\prime }=-{\sin }^{-2}x\cdot \cos x=-\csc x\cdot \cot x$$

$$({\mathrm{a}}^x{)}^{\prime }={\mathrm{a}}^x\cdot \ln a,(\mathrm{a}>0,a\ne 1).$$

$$({\mathrm{e}}^x{)}^{\prime }={\mathrm{e}}^x$$

$$({\log }_{a}x{)}^{\prime }=\frac{1}{x\cdot \ln a},(a>0,a\ne 1).$$

$$(\ln x{)}^{\prime }=\frac{1}{x}$$

$$(\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}$$

$$(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$$

$$(\arctan x{)}^{\prime }=\frac{1}{1+x^2}$$

$$(\mathrm{arccot}x{)}^{\prime }=-\frac{1}{1+x^2}$$

---

函数的和、差、积、商的求导法则：

设 $u=u(x)$, $v=v(x)$ 都可导，则

（1）$(u\pm v{)}^{\prime }=u^{\prime }\pm v^{\prime }$.

（2）$(\mathrm{C}u{)}^{\prime }=\mathrm{C}{u}^{\prime },(\mathrm{C}是常数).$

（3）$(uv{)}^{\prime }=u^{\prime }v+u{v}^{\prime }$.

（4）$(\frac{u}{v}{)}^{\prime }=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}$.

---

反函数的求导法则：

设 $x=f(y)$ 在区间 $I_y$ 内单调可导（单调才能有反函数），且 $f(y)\ne 0$，则它的反函数 $y=f^{-1}(x)$ 在 $I_x=f(I_y)$ 内也可导，则：
$$[f^{-1}(x){]}^{\prime }=\frac{1}{f^{\prime }(y)}或\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}.$$

也就是说，反函数的导数等于直接函数导数的倒数。

用函数图像来解释，应该更容易理解。对于 $y=f(x)$ ，导数在图像上表现为函数图像曲线某点的切线，即函数图像在该点处的斜率。而反函数 $x=f^{-1}(y)$ 的图像和直接函数 $y=f(x)$ 的图像关于直线 $y=x$ 对称，即将 $x$ 轴和 $y$ 反转，斜率 $k=\frac{\Delta y}{\Delta x},(\Delta x\to 0)$ ，当图像关于直线 $y=x$ 对称反转后，在同一点处的斜率互为倒数关系 $k^{\prime }=\frac{1}{k}=\frac{\Delta x}{\Delta y}$. 所以，反函数的导数等于直接函数导数的倒数。

设 $x=\sin y$，$y\in [-\frac{\pi }{2},\frac{\pi }{2}]$ 为直接函数，则 $y=\arcsin x$ 是它们的反函数. $x=\sin y$ 在开区间 $I_y=(-\frac{\pi }{2},\frac{\pi }{2})$ 内单调、可导，且 $(\sin y{)}^{\prime }=\cos y>0$. 在对应区间 $I_x=(-1,1)$ 上有 $y^{\prime }=(\arcsin x{)}^{\prime }=\frac{1}{x^{\prime }}=\frac{1}{\cos y}$.

$\cos y=\sqrt{1-{\sin }^{2}y}=\sqrt{1-x^2}$.

$\therefore y^{\prime }=(\arcsin x{)}^{\prime }=\frac{1}{x^{\prime }}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-x^2}}$.

同样地，对于 $x=\cos y$, $y\in [0,\pi ]$ 为直接函数，则 $y=\arccos x$ 是它的反函数. $x=\cos y$ 在开区间 $I_y=(0,\pi )$ 内单调、可导，且 $(\cos y{)}^{\prime }=-\sin y<0$. 在对应的区间 $I_x=(-1,1)$ 上有 $y^{\prime }=(\arccos x{)}^{\prime }=\frac{1}{x^{\prime }}=-\frac{1}{\sin y}$.

$\sin y=\sqrt{1-{\cos }^{2}y}=\sqrt{1-x^2}$.

$\therefore y^{\prime }=(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$.

---

复合函数求导法则：
设 $y=f(u)$，而 $u=g(x)$ 且 $f(u)$ 及 $g(x)$ 都可导，则复合函数 $y=f[g(x)]$ 的导数为 $y^{\prime }=f^{\prime }(u)\cdot g^{\prime }(x)$. 或 $y^{\prime }=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\cdot \frac{\mathrm{d}u}{\mathrm{d}x}$.