有限元方法在求解PED时，一般先将控制方程转化为等效的若积分形式，本文试图总结一下这一过程的一些数学基础，本文主要从工程的角度出发和理解，不探讨严谨的数学证明过程。

PDE强形式

强形式是PDE及其边界条件的原始形式。求解强形式问题要求解函数满足方程及其边界条件中的所有微分算子和约束。
例如一维泊松方程：
$-\frac{d^{2}u}{d{x}^2}=f\text{in}(0,1)$
边界条件为：
$u(0)=u(1)=0$
例如弹性力学中的平衡方程：
$\nabla \cdot \sigma +b=0\text{in}\Omega$
边界条件为：
$u=0\text{on}\partial {\Omega }_u$ $\sigma \cdot n=t\text{on}\partial {\Omega }_t$
大部分的PDE方程都很难搞，无法直接求得解析解，只能从逼近的角度求得近似数值解，再进行数值求解之前，一般需要弄一个试探函数， 试探函数给定了一些基函数的形式但是系数待定，通过让试探函数满足控制方程来获取一组方程从而求解系数。这里面有一个较大的问题就是，PDE中一般含有高阶导数想，如果想让试探函数满足PDE方程，那么对试探函数的连续性要求就比较高，如果通过一定的方式对方称进行转换，降低对试函数的连续性要求，将会对方程的求解带来极大地方便。

等效积分和弱形式

偏微分方程的等效积分形式是通过乘以一个权函数并在定义域上积分得到的。这一形式通过将原始的偏微分方程转化为一个积分方程，能够更容易地处理边界条件并降低对解的光滑性要求。

下面以泊松方程为例详细说明这个过程。

强形式

考虑一个定义在区域 $\Omega$ 上的泊松方程：
$-\Delta u=f\text{在}\Omega$
有Dirichlet边界条件：
$u=0\text{在}\partial \Omega$

弱形式的推导

乘以测试函数：选择一个适当的测试函数 $v\in H_0^1(\Omega )$（在 $\partial \Omega$ 上为零的平方可积函数），并将泊松方程乘以 $v$：$-\Delta u\cdot v=f\cdot v$

在定义域上积分：对上述等式在定义域 $\Omega$ 上积分：${\int }_{\Omega }(-\Delta u)vd\Omega ={\int }_{\Omega }fvd\Omega$

应用分部积分（高斯定理）：为了简化左边的积分，我们应用分部积分（也称为高斯散度定理）：
${\int }_{\Omega }(-\Delta u)vd\Omega ={\int }_{\Omega }\nabla \cdot (\nabla u)vd\Omega ={\int }_{\partial \Omega }(\nabla u\cdot \mathbf{n})vdS-{\int }_{\Omega }\nabla u\cdot \nabla vd\Omega$
其中，$\mathbf{n}$ 是$\Omega$ 的外法向量，$\partial \Omega 是\Omega$的边界。由于$v$在边界$\partial \Omega$ 上为零，边界项消失，因此：${\int }_{\Omega }(-\Delta u)vd\Omega =-{\int }_{\Omega }\nabla u\cdot \nabla vd\Omega$

得到等效弱形式：结合右边的积分，我们得到泊松方程的弱形式：${\int }_{\Omega }\nabla u\cdot \nabla vd\Omega ={\int }_{\Omega }fvd\Omega$
在这个弱形式中，求解的函数 $u$ 只需要在区域 $\Omega$内具有一阶导数的平方可积性，而不需要具有二阶连续导数。这使得弱形式在有限元方法中具有广泛的应用，因为它降低了对解的光滑性要求，并且能够自然地处理边界条件。

再来看一个弹性力学平衡方程的弱积分形式

弹性力学平衡方程

假设我们有一个弹性体，定义在区域 $\Omega$ 上，具有以下强形式的平衡方程：
$\nabla \cdot \sigma +b=0\text{在}\Omega$
这里 $\sigma$ 是应力张量，$b$ 是体力密度。
假设边界条件包括：

• Dirichlet 边界条件：位移 $u=0$ 在边界 ${\Gamma }_u$ 上。
• Neumann 边界条件：表面力 $\sigma \cdot n=t$ 在边界 ${\Gamma }_t$ 上，其中 $n$ 是外法向量。
  

弱形式推导

乘以测试函数：选择一个适当的测试函数 $v\in [H_0^1(\Omega ){]}^n$，并将平衡方程乘以 $v$：$(\nabla \cdot \sigma +b)\cdot v=0$

在定义域上积分：对上述等式在定义域 $\Omega$ 上积分：${\int }_{\Omega }(\nabla \cdot \sigma )\cdot vd\Omega +{\int }_{\Omega }b\cdot vd\Omega =0$

应用分部积分（高斯散度定理）：为了简化第一项的积分，我们应用分部积分（高斯散度定理）：${\int }_{\Omega }(\nabla \cdot \sigma )\cdot vd\Omega =-{\int }_{\Omega }\sigma :\nabla vd\Omega +{\int }_{\partial \Omega }(\sigma \cdot n)\cdot vdS$
其中，$\partial \Omega$ 是 $\Omega$ 的边界，由于 $\partial \Omega ={\Gamma }_u\cup {\Gamma }_t$，
我们有：${\int }_{\partial \Omega }(\sigma \cdot n)\cdot vdS={\int }_{{\Gamma }_t}t\cdot vdS+{\int }_{{\Gamma }_u}(\sigma \cdot n)\cdot vdS$
注意到在 ${\Gamma }_u$ 上，测试函数 $v=0$，所以：${\int }_{{\Gamma }_u}(\sigma \cdot n)\cdot vdS=0$
因此：${\int }_{\partial \Omega }(\sigma \cdot n)\cdot vdS={\int }_{{\Gamma }_t}t\cdot vdS$

得到弱积分形式：结合右边的积分，我们得到平衡方程的弱积分形式：$-{\int }_{\Omega }\sigma :\nabla vd\Omega +{\int }_{\Omega }b\cdot vd\Omega +{\int }_{{\Gamma }_t}t\cdot vdS=0$
代入应力-应变关系 $\sigma =\mathbb{C}:ϵ$，并且 $ϵ=\frac{1}{2}(\nabla u+(\nabla u{)}^T)$
我们有：$-{\int }_{\Omega }(\mathbb{C}:ϵ):\nabla vd\Omega +{\int }_{\Omega }b\cdot vd\Omega +{\int }_{{\Gamma }_t}t\cdot vdS=0$
注意到 $ϵ:\nabla v=\frac{1}{2}(\nabla u+(\nabla u{)}^T):\nabla v=\nabla u:\nabla v$，
我们得到：${\int }_{\Omega }\mathbb{C}:(\nabla u:\nabla v)d\Omega ={\int }_{\Omega }b\cdot vd\Omega +{\int }_{{\Gamma }_t}t\cdot vdS$

弹性力学平衡方程的弱积分形式
${\int }_{\Omega }\mathbb{C}:(\nabla u:\nabla v)d\Omega ={\int }_{\Omega }b\cdot vd\Omega +{\int }_{{\Gamma }_t}t\cdot vdS\forall v\in [H_0^1(\Omega ){]}^n$

在这个弱积分形式中降低了对解的光滑性要求，使得问题可以在更广泛的函数空间中讨论，并且能够自然地处理边界条件，处理积分时边界项可以自然地引入力的边界条件。在有限元方法中，弱形式为数值求解提供了方便和稳定性。这种形式在工程和科学计算中具有广泛的应用。

降阶的思想

上面的若积分形式推导过程中，有一个关键的地方是利用分部积分将含有最高二阶导数的控制方程转换为只含有最高一阶导数的积分形式。这样对函数$u$只需要求较低阶的连续性就可以了。这种降阶是以提高测试函数$v$的连续性要求为代价的，但是适当提高其连续性的要求并不困难，因为它们是可以选择的已知函数。这种通过适当提高对任意函数$v$ 的连续性要求，以降低对微分方程场函数 u 的连续性要求所建立的等效积分形式称为微分方程的等效积分“弱”形式。它在近似计算中，尤其是在有限单元法中是十分重要的。值得指出的是，从形式上看“弱”形式对函数u的连续性要求降低了， 但对实际的物理问题却常常较原始的微分方程更通近真正解，因为原始微分方程往往对解提出了过分“平滑”的要求。

试函数连续性要求

对于一个C0连续的函数，其一阶导数和二阶导数是存在间断点的，如果对间断点附近进行光滑过度，那么一阶导数变得连续，二阶导数则可能出现无穷大。

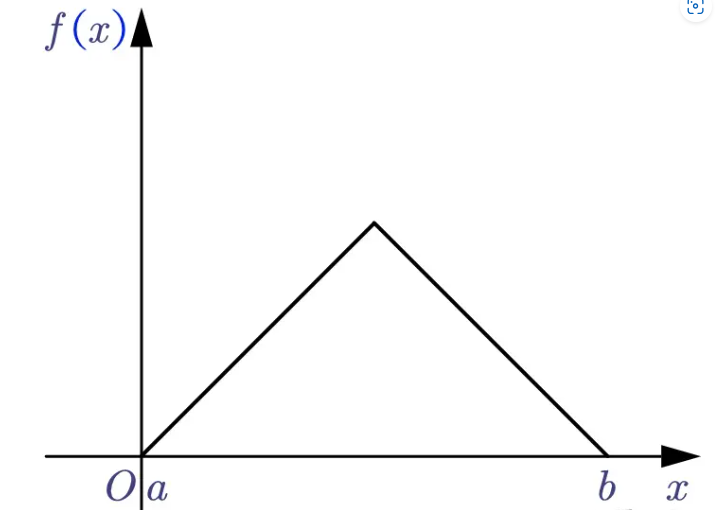
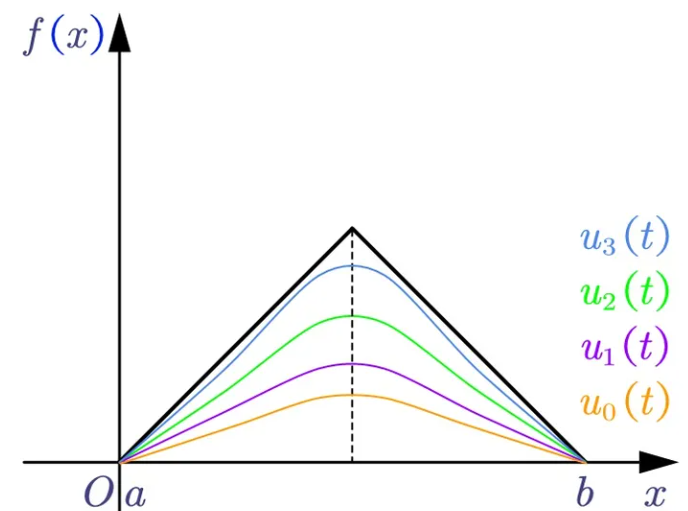
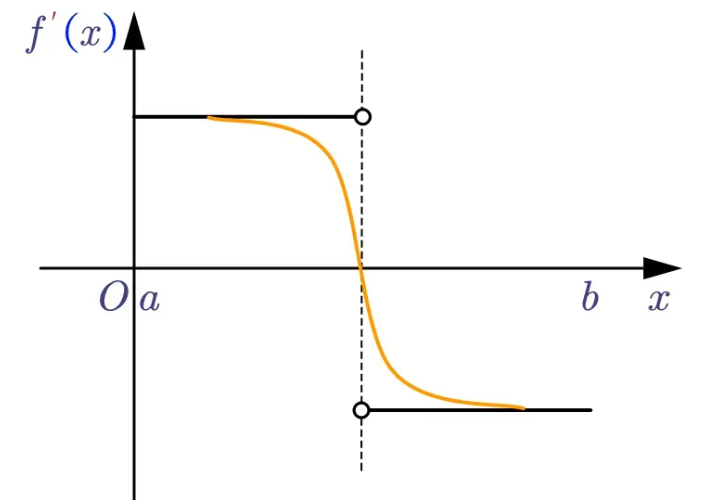
看如下更具体一点的例子，这个分段线性函数$f(x)$存在一个一阶导数不连续点，如果用一个光滑函数序列去无线逼近$f(x)$函数，光滑函数的导数也将无限逼近$f^{\prime }(x)$，直观上看光滑函数导数围成的面积和$f^{\prime }(x)$围成的面积接近。

不是一般性，我们总结一下：
如果弱形式积分方程含有最高二阶导数，那么要求试探函数满足C1连续，因为C1连续函数的一阶导数连续，二阶导数可求(不一定连续)， 若只有C0连续，那么二阶导数可能会出现无穷大。
如果弱形式积分方程含有最高一阶导数，那么要求试探函数满足C0连续，弱不连续，则一阶导数可能会出现无穷大情况。

弱导数的思想

其实上面对连续性的要求暗含了弱导数的思想，对于C0函数，虽然一阶导数存在间断点，但是我们可以引入弱导数的概念，将导数的概念泛化，从而解决了数学理论上的一些棘手问题。

定义

设 $f$ 是一个定义在开区间 $\Omega \subset \mathbb{R}$ 上的可积函数。若存在一个可积函数 $g$，使得对于任意一个紧支撑 $\phi \in C_c^{\infty }(\Omega )$（$\Omega$上紧支撑的无限可微函数，紧支撑即在边界处为0），以下积分恒等式成立：
${\int }_{\Omega }f(x){\phi }^{\prime }(x)dx=-{\int }_{\Omega }g(x)\phi (x)dx$
则称 $g$ 是 $f$ 的弱导数，记作 $g=f^{\prime };$ 或 $g=\frac{d}{dx}f$。

直观理解

弱导数的定义意味着我们通过积分的形式来定义导数，使其能够应用于传统意义上不可导的函数。我们通过测试函数 $\phi$ 的积分来“探测” $f$ 的导数。

示例

考虑 $f(x)=|x|$ 在区间 $(-1,1)$ 上的情况。

1. $f(x)=|x|$ 在 $x=0$ 处不可导，但在其他地方是可导的。
2. $f(x)$ 的传统导数 $f^{\prime }(x)$ 在 $x=0$ 处不定义，但弱导数可以定义。

我们先计算 ${\int }_{-1}^1|x|{\phi }^{\prime }(x)dx$。
由于 $|x|$ 在 $x=0$ 处不可导，我们将积分分成两部分：

${\int }_{-1}^1|x|{\phi }^{\prime }(x)dx={\int }_{-1}^0(-x){\phi }^{\prime }(x)dx+{\int }_0^{1}x{\phi }^{\prime }(x)dx$

对每个部分进行分部积分：

${\int }_{-1}^0(-x){\phi }^{\prime }(x)dx={\left[-x\phi (x)\right]}_{-1}^0+{\int }_{-1}^0\phi (x)dx={\int }_{-1}^0\phi (x)dx$ ${\int }_0^{1}x{\phi }^{\prime }(x)dx={\left[x\phi (x)\right]}_0^1-{\int }_0^1\phi (x)dx=-{\int }_0^1\phi (x)dx$

所以：

${\int }_{-1}^1|x|{\phi }^{\prime }(x)dx={\int }_{-1}^0\phi (x)dx-{\int }_0^1\phi (x)dx$

合并积分：
${\int }_{-1}^1|x|{\phi }^{\prime }(x)dx={\int }_{-1}^1\text{sgn}(x)\phi (x)dx$

这里，$\text{sgn}(x)$ 是符号函数，定义为：

$\text{sgn}(x)=\{\begin{array}{ll}-1,& x<0\\ 0,& x=0\\ 1,& x>0\end{array}$

因此，我们得出：
${\int }_{-1}^1|x|{\phi }^{\prime }(x)dx=-{\int }_{-1}^1\text{sgn}(x)\phi (x)dx$
这表明：

$\frac{d}{dx}|x|=\text{sgn}(x)$

弱导数的概念使我们能够处理不具备传统导数的函数。通过积分形式定义导数，我们可以在更广泛的函数空间中讨论导数的概念。这在有限元分析、偏微分方程等领域中有重要应用。弱导数使得我们能够对不可导函数进行分析和计算。许多实际问题中，涉及的函数可能在某些点上不可导，但仍然可以定义其弱导数。例如撒花姑娘面的例子$f(x)=|x|$ 在 $x=0$ 处不可导，但其弱导数存在且等于符号函数 $\text{sgn}(x)$。