文章目录
- 决策单调性
- 四边形不等式
- 决策单调性
- 形式1
- 法1 分治
- 法2 二分队列
- 例题 P3515
- Solution
- 形式2
- 例题 P3195
- Solution
- 形式3
- 例题 CF833B
- Solution
- 形式4
- 例题
- Solution
- 后话
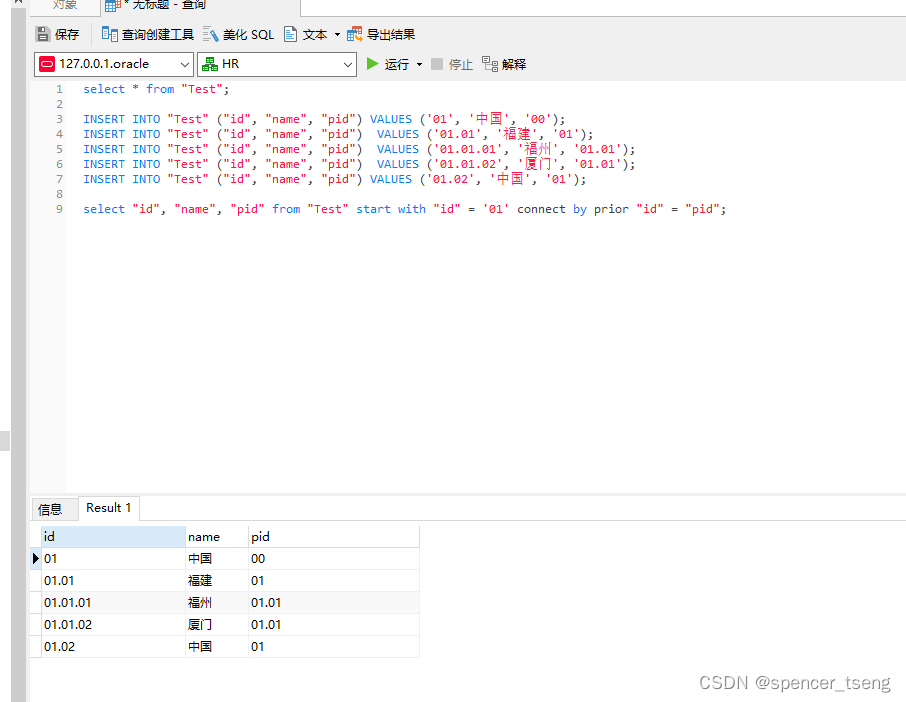
决策单调性
四边形不等式
定义:
对于二元函数
w
(
x
,
y
)
w(x,y)
w(x,y),若
∀
a
,
b
,
c
,
d
∈
Z
\forall a,b,c,d\in \mathbb{Z}
∀a,b,c,d∈Z,且
a
≤
b
≤
c
≤
d
a\le b\le c\le d
a≤b≤c≤d,都有
w
(
a
,
d
)
+
w
(
b
,
c
)
≥
w
(
a
,
c
)
+
w
(
b
,
d
)
w(a,d)+w(b,c)\ge w(a,c)+w(b,d)
w(a,d)+w(b,c)≥w(a,c)+w(b,d),则称函数
w
w
w 满足四边形不等式,也称它满足凸完全单调性
简记为 跨越 + + + 包含 ≥ \ge ≥ 交叉
定理1:
若函数 w ( x , y ) w(x,y) w(x,y) 满足 ∀ a , b ∈ Z , a < b \forall a,b\in \mathbb{Z},a<b ∀a,b∈Z,a<b 都有 w ( a , b + 1 ) + w ( a + 1 , b ) ≥ w ( a , b ) + w ( a + 1 , b + 1 ) w(a,b+1)+w(a+1,b)\ge w(a,b)+w(a+1,b+1) w(a,b+1)+w(a+1,b)≥w(a,b)+w(a+1,b+1)
则函数 w w w 满足四边形不等式
证明1:
若 a < c a<c a<c,有 w ( a , c + 1 ) + w ( a + 1 , c ) ≥ w ( a , c ) + w ( a + 1 , c + 1 ) w(a,c+1)+w(a+1,c)\ge w(a,c)+w(a+1,c+1) w(a,c+1)+w(a+1,c)≥w(a,c)+w(a+1,c+1)
若 a + 1 < c a+1<c a+1<c,有 w ( a + 1 , c + 1 ) + w ( a + 2 , c ) ≥ w ( a + 1 , c ) + w ( a + 2 , c + 1 ) w(a+1,c+1)+w(a+2,c)\ge w(a+1,c)+w(a+2,c+1) w(a+1,c+1)+w(a+2,c)≥w(a+1,c)+w(a+2,c+1)
两式相加,得 w ( a , c + 1 ) + w ( a + 1 , c ) + w ( a + 1 , c + 1 ) + w ( a + 2 , c ) ≥ w ( a , c ) + w ( a + 1 , c + 1 ) + w ( a + 1 , c ) + w ( a + 2 , c + 1 ) w(a,c+1)+w(a+1,c)+w(a+1,c+1)+w(a+2,c)\ge w(a,c)+w(a+1,c+1)+w(a+1,c)+w(a+2,c+1) w(a,c+1)+w(a+1,c)+w(a+1,c+1)+w(a+2,c)≥w(a,c)+w(a+1,c+1)+w(a+1,c)+w(a+2,c+1)
即 w ( a , c + 1 ) + w ( a + 2 , c ) ≥ w ( a , c ) + w ( a + 2 , c + 1 ) w(a,c+1)+w(a+2,c)\ge w(a,c)+w(a+2,c+1) w(a,c+1)+w(a+2,c)≥w(a,c)+w(a+2,c+1)
同理可证, ∀ a ≤ b ≤ c , w ( a , c + 1 ) + w ( b , c ) ≥ w ( a , c ) , w ( b , c + 1 ) \forall a\le b\le c,w(a,c+1)+w(b,c)\ge w(a,c),w(b,c+1) ∀a≤b≤c,w(a,c+1)+w(b,c)≥w(a,c),w(b,c+1)
同理可证, ∀ a ≤ b ≤ c ≤ d \forall a\le b\le c\le d ∀a≤b≤c≤d, w ( a , d ) + w ( b , c ) ≥ w ( a , c ) + w ( b , d ) w(a,d)+w(b,c)\ge w(a,c)+w(b,d) w(a,d)+w(b,c)≥w(a,c)+w(b,d)
决策单调性
定义:
考虑转移方程
f
[
i
]
=
min
0
≤
j
<
i
(
f
[
j
]
+
w
(
j
,
i
)
)
f[i]=\min_{0\le j <i} (f[j]+w(j,i))
f[i]=min0≤j<i(f[j]+w(j,i))
令
p
[
i
]
p[i]
p[i] 表示
i
i
i 的最优决策
j
j
j,即让
f
[
i
]
f[i]
f[i] 取最小值的 最小
j
j
j
若
p
[
i
]
p[i]
p[i] 在
[
1
,
n
]
[1,n]
[1,n] 上单调不减,则称
f
f
f 具有决策单调性
定理2:
考虑转移方程 f [ i ] = min 0 ≤ j < i ( f [ j ] + w ( j , i ) ) f[i]=\min_{0\le j <i} (f[j]+w(j,i)) f[i]=min0≤j<i(f[j]+w(j,i)),若函数 w w w 满足四边形不等式,则 f f f 具有决策单调性
证明2:
∀ i ∈ [ 1 , n ] , j ∈ [ 0 , p [ i ] − 1 ] , f [ p [ i ] ] + w ( p [ i ] , i ) ≤ f [ j ] + w ( j , i ) \forall i\in [1,n],j\in[0,p[i]-1],f[p[i]]+w(p[i],i)\le f[j]+w(j,i) ∀i∈[1,n],j∈[0,p[i]−1],f[p[i]]+w(p[i],i)≤f[j]+w(j,i) ( 1 ) \color{red}(1) (1)
∀ i ′ ∈ [ i + 1 , n ] , j < p [ i ] < i < i ′ , w ( j , i ′ ) + w ( p [ i ] , i ) ≥ w ( j , i ) + w ( p [ i ] , i ′ ) \forall i'\in [i+1,n],j<p[i]<i<i',w(j,i')+w(p[i],i)\ge w(j,i)+w(p[i],i') ∀i′∈[i+1,n],j<p[i]<i<i′,w(j,i′)+w(p[i],i)≥w(j,i)+w(p[i],i′)
∴ w ( p [ i ] , i ′ ) − w ( p [ i ] , i ) ≤ w ( j , i ′ ) − w ( j , i ) \therefore w(p[i],i')-w(p[i],i)\le w(j,i')-w(j,i) ∴w(p[i],i′)−w(p[i],i)≤w(j,i′)−w(j,i) ( 2 ) \color{red}(2) (2)
( 1 ) \color{red}(1) (1)+ ( 2 ) \color{red}(2) (2) 得: f [ p [ i ] ] + w ( p [ i ] , i ′ ) ≤ f [ j ] + w ( j , i ′ ) f[p[i]]+w(p[i],i')\le f[j]+w(j,i') f[p[i]]+w(p[i],i′)≤f[j]+w(j,i′)
∴ p [ i ′ ] ≥ p [ i ] \color{red} \therefore p[i']\ge p[i] ∴p[i′]≥p[i]
所以 f f f 具有决策单调性
形式1
用于优化形如
f
[
i
]
=
min
1
≤
j
≤
i
w
(
j
,
i
)
f[i]=\min_{1\le j\le i} w(j,i)
f[i]=min1≤j≤iw(j,i) 的转移方程。
因为我们只需要找到每一个
p
[
i
]
p[i]
p[i],我们就可以算出每一个
f
[
i
]
f[i]
f[i] 了,那么对于这种方法,我们有两种常见方法。
法1 分治
考虑求区间
[
1
,
n
]
[1,n]
[1,n] 的
p
[
i
]
p[i]
p[i],我们先求出
p
[
m
i
d
]
p[mid]
p[mid],再把它分成两个区间
[
1
,
m
i
d
−
1
]
[1,mid-1]
[1,mid−1] 和
[
m
i
d
+
1
,
n
]
[mid+1,n]
[mid+1,n] 分治求解。
为什么可以呢,因为根据决策单调性,
∀
i
∈
[
m
i
d
+
1
,
n
]
,
p
[
i
]
≥
p
[
m
i
d
]
,
∀
j
∈
[
1
,
m
i
d
−
1
]
,
p
[
j
]
≤
p
[
m
i
d
]
\forall i\in[mid+1,n],p[i]\ge p[mid],\forall j\in [1,mid-1],p[j]\le p[mid]
∀i∈[mid+1,n],p[i]≥p[mid],∀j∈[1,mid−1],p[j]≤p[mid]
所以可以分治来求答案。
参考代码:
void solve(int l,int r,int pl,int pr){
// 求pmid=p[mid]
//算出 f[mid]
solve(l,mid-1,p,pmid);
solve(mid+1,r,pmid,pr);
}
法2 二分队列
易证,每一个决策一定是在一个区间内的,例如:
p
[
i
]
(
i
∈
[
1
,
4
]
)
=
1
,
p
[
i
]
(
i
∈
[
5
,
9
]
)
=
3
,
p
[
i
]
(
i
∈
[
10
,
n
]
)
=
k
p[i](i\in[1,4])=1,p[i](i\in[5,9])=3,p[i](i \in[10,n])=k
p[i](i∈[1,4])=1,p[i](i∈[5,9])=3,p[i](i∈[10,n])=k
所以可以维护一个单调队列,用于表示每个决策
i
i
i 所对应的最优转移点。
参考代码:
void solve(){
h=1,t=0;
for(int i=1;i<=n;i++){
insert(i);
if(h<=t&&q[h].r<i)
h++;
else
q[h].l=i;
f[i]=min(f[i],w(q[h].p,i));
}
}
例题 P3515
给定一个长度为 n n n 的序列 { a n } \{a_n\} {an},对于每个 i ∈ [ 1 , n ] i\in [1,n] i∈[1,n] ,求出一个最小的非负整数 p p p ,使得 ∀ j ∈ [ 1 , n ] \forall j\in[1,n] ∀j∈[1,n],都有 a j ≤ a i + p − ∣ i − j ∣ a_j\le a_i+p-\sqrt{|i-j|} aj≤ai+p−∣i−j∣
1 ≤ n ≤ 5 × 1 0 5 1 \le n \le 5\times 10^{5} 1≤n≤5×105, 0 ≤ a i ≤ 1 0 9 0 \le a_i \le 10^{9} 0≤ai≤109 。
Solution
先变形:
p
≥
a
[
j
]
+
∣
i
−
j
∣
−
a
[
i
]
,
∀
j
∈
[
1
,
n
]
p\ge a[j]+\sqrt{|i-j|}-a[i],\forall j\in[1,n]
p≥a[j]+∣i−j∣−a[i],∀j∈[1,n]
问题变为求 max ( a [ j ] + ∣ i − j ∣ ) , ∀ j ∈ [ 1 , n ] \max(a[j]+\sqrt{|i-j|}),\forall j\in[1,n] max(a[j]+∣i−j∣),∀j∈[1,n]
考虑将序列先算一遍,翻转一次后再算一遍,最后求最大值,即变为求 max ( a [ j ] + ∣ i − j ∣ ) , ∀ j ∈ [ 1 , i ] \max(a[j]+\sqrt{|i-j|}),\forall j\in[1,i] max(a[j]+∣i−j∣),∀j∈[1,i]
令
f
[
i
]
=
max
(
a
[
j
]
+
i
−
j
)
f[i]=\max(a[j]+\sqrt{i-j})
f[i]=max(a[j]+i−j)
此处
w
(
j
,
i
)
=
i
−
j
w(j,i)=\sqrt{i-j}
w(j,i)=i−j
定义
a
+
1
<
c
a+1<c
a+1<c
则有:
w
(
a
,
c
)
=
c
−
a
,
w
(
a
+
1
,
c
)
=
c
−
a
−
1
,
w
(
a
,
c
+
1
)
=
c
−
a
+
1
,
w
(
a
+
1
,
c
+
1
)
=
c
−
a
w(a,c)=\sqrt{c-a},w(a+1,c)=\sqrt{c-a-1},w(a,c+1)=\sqrt{c-a+1},w(a+1,c+1)=\sqrt{c-a}
w(a,c)=c−a,w(a+1,c)=c−a−1,w(a,c+1)=c−a+1,w(a+1,c+1)=c−a
∴
w
(
a
,
c
+
1
)
+
w
(
a
+
1
,
c
)
−
w
(
a
,
c
)
−
w
(
a
+
1
,
c
+
1
)
=
c
−
a
−
1
+
c
−
a
+
1
−
2
c
−
a
\therefore w(a,c+1)+w(a+1,c)-w(a,c)-w(a+1,c+1)=\sqrt{c-a-1}+\sqrt{c-a+1}-2\sqrt{c-a}
∴w(a,c+1)+w(a+1,c)−w(a,c)−w(a+1,c+1)=c−a−1+c−a+1−2c−a
令
d
=
c
−
a
d=c-a
d=c−a
原式
=
(
d
+
1
−
d
)
−
(
d
−
d
−
1
)
=(\sqrt{d+1}-\sqrt{d})-(\sqrt{d}-\sqrt{d-1})
=(d+1−d)−(d−d−1)
对函数
f
(
x
)
=
x
−
x
−
1
f(x)=\sqrt{x}-\sqrt{x-1}
f(x)=x−x−1 求导发现其单调递减,所以原式恒小于
0
0
0,即可得:
w
(
a
,
c
+
1
)
+
w
(
a
+
1
,
c
)
≤
w
(
a
,
c
)
+
w
(
a
+
1
,
c
+
1
)
w(a,c+1)+w(a+1,c)\le w(a,c)+w(a+1,c+1)
w(a,c+1)+w(a+1,c)≤w(a,c)+w(a+1,c+1)
可以发现,它跟四边形不等式符号相反,同样亦可证得
f
f
f 满足决策单调性,于是可以套用 法
1
1
1 和法
2
2
2 进行求解。
参考代码:
F1:
#include<bits/stdc++.h>
#define int __int128
#define lf double
using namespace std;
const int N=5e5+1,mod=1e9+7;
const lf eps=1e-5;
int n,a[N];
lf sq[N],f[N];
inline lf w(int j,int i){
return 1.0*a[j]+sq[i-j];
}
inline int Ceil(lf x){
return (int)(x+1-eps);
}
void solve(int l,int r,int pl,int pr){
if(l>r)
return ;
int mid=(l+r)>>1,mxp;
lf mx=0;
for(int i=pl;i<=min(mid,pr);i++)
if(w(i,mid)>mx)
mx=w(i,mid),mxp=i;
f[mid]=max(f[mid],mx);
solve(l,mid-1,pl,mxp);
solve(mid+1,r,mxp,pr);
}
signed main(){
n=read();
for(int i=1;i<=n;i++)
a[i]=read(),sq[i]=sqrt((1.0*i));
solve(1,n,1,n);
for(int i=1;i<=n/2;i++)
swap(a[i],a[n-i+1]),swap(f[i],f[n-i+1]);
solve(1,n,1,n);
for(int i=1;i<=n/2;i++)
swap(a[i],a[n-i+1]),swap(f[i],f[n-i+1]);
for(int i=1;i<=n;i++){
write(Ceil(f[i]-a[i]));
printf("\n");
}
return 0;
}
F2:
#include<bits/stdc++.h>
#define int __int128
#define lf double
using namespace std;
const int N=5e5+1,mod=1e9+7;
const lf eps=1e-5;
int n,a[N],h,t;
lf sq[N],f[N];
struct fy{
int l,r,p;
}q[N];
inline lf w(int j,int i){
return 1.0*a[j]+sq[i-j];
}
inline int Ceil(lf x){
return (int)(x+1-eps);
}
int find_(int t,int x){
int res=q[t].r+1,l=q[t].l,r=q[t].r,p=q[t].p;
while(l<=r){
int mid=(l+r)>>1;
if(w(p,mid)<=w(x,mid))
res=mid,r=mid-1;
else
l=mid+1;
}
return res;
}
void insert(int x){
q[t].l=max(q[t].l,x);
while(h<=t&&w(q[t].p,q[t].l)<=w(x,q[t].l))
t--;
if(h<=t){
int mid=find_(t,x);
if(mid>n)
return ;
q[t].r=mid-1;
q[++t].l=mid,q[t].p=x,q[t].r=n;
}
else{
q[++t].l=x,q[t].p=x,q[t].r=n;
}
}
void solve(){
h=1,t=0;
for(int i=1;i<=n;i++){
insert(i);
if(h<=t&&q[h].r<i)
h++;
else
q[h].l=i;
f[i]=max(f[i],w(q[h].p,i));
}
}
signed main(){
n=read();
for(int i=1;i<=n;i++)
a[i]=read(),sq[i]=sqrt((1.0*i));
solve();
for(int i=1;i<=n/2;i++)
swap(a[i],a[n-i+1]),swap(f[i],f[n-i+1]);
solve();
for(int i=1;i<=n/2;i++)
swap(a[i],a[n-i+1]),swap(f[i],f[n-i+1]);
for(int i=1;i<=n;i++){
write(Ceil(f[i]-a[i]));
printf("\n");
}
return 0;
}
形式2
用于优化形如
f
[
i
]
=
min
0
≤
j
<
i
(
f
[
j
]
+
w
(
j
+
1
,
i
)
)
f[i]=\min_{0\le j<i}(f[j]+w(j+1,i))
f[i]=min0≤j<i(f[j]+w(j+1,i)) 的转移方程。(
w
w
w 满足四边形不等式)
注意到此种转移方程依赖于前面的值,因此分治法不再适用,所以只能用二分队列,思路跟上面一摸一样。
例题 P3195
P 教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。
P 教授有编号为
1
⋯
n
1 \cdots n
1⋯n 的
n
n
n 件玩具,第
i
i
i 件玩具经过压缩后的一维长度为
C
i
C_i
Ci。
为了方便整理,P教授要求:
- 在一个一维容器中的玩具编号是连续的。
- 同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第
i
i
i 件玩具到第
j
j
j 个玩具放到一个容器中,那么容器的长度将为
x
=
j
−
i
+
∑
k
=
i
j
C
k
x=j-i+\sum\limits_{k=i}^{j}C_k
x=j−i+k=i∑jCk。
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 x x x,其制作费用为 ( x − L ) 2 (x-L)^2 (x−L)2。其中 L L L 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 L L L。但他希望所有容器的总费用最小。
对于全部的测试点, 1 ≤ n ≤ 5 × 1 0 4 1 \leq n \leq 5 \times 10^4 1≤n≤5×104, 1 ≤ L ≤ 1 0 7 1 \leq L \leq 10^7 1≤L≤107, 1 ≤ C i ≤ 1 0 7 1 \leq C_i \leq 10^7 1≤Ci≤107。
Solution
令
f
[
i
]
f[i]
f[i] 表示前
i
i
i 个玩具装箱的最小代价,则枚举第
i
i
i 个玩具和那些玩具放在一个箱子中,可得转移方程:
f
[
i
]
=
min
1
≤
j
≤
i
(
f
[
j
−
1
]
+
(
i
−
j
−
L
+
∑
k
=
j
i
C
k
)
2
)
f[i]=\min_{1\le j\le i}(f[j-1]+(i-j-L+\sum_{k=j}^iC_k)^2)
f[i]=1≤j≤imin(f[j−1]+(i−j−L+k=j∑iCk)2)
f
f
f 满足决策单调性,证明参考 OI-WIKI

补充:图片的
K
K
K 与题意中的
L
L
L 意思相同。
性质
1
,
2
,
3
1,2,3
1,2,3:

那么把形式
1
1
1 例题的方法
2
2
2 的代码改装一下就可以了。
参考Code:
#include<bits/stdc++.h>
#define int __int128
#define lf double
using namespace std;
const int N=5e5+1,mod=1e9+7;
const lf eps=1e-5;
int n,a[N],h,t,L;
int f[N],sum[N];
struct fy{
int l,r,p;
}q[N];
inline int w(int j,int i){
return f[j-1]+(i-j+sum[i]-sum[j-1]-L)*(i-j+sum[i]-sum[j-1]-L);
}
int find_(int t,int x){
int res=q[t].r+1,l=q[t].l,r=q[t].r,p=q[t].p;
while(l<=r){
int mid=(l+r)>>1;
if(w(p,mid)>=w(x,mid))
res=mid,r=mid-1;
else
l=mid+1;
}
return res;
}
void insert(int x){
q[t].l=max(q[t].l,x);
while(h<=t&&w(q[t].p,q[t].l)>=w(x,q[t].l))
t--;
if(h<=t){
int mid=find_(t,x);
if(mid>n)
return ;
q[t].r=mid-1;
q[++t].l=mid,q[t].p=x,q[t].r=n;
}
else{
q[++t].l=x,q[t].p=x,q[t].r=n;
}
}
void solve(){
h=1,t=0;
for(int i=1;i<=n;i++){
insert(i);
if(h<=t&&q[h].r<i)
h++;
else
q[h].l=i;
f[i]=max(f[i],w(q[h].p,i));
}
}
signed main(){
n=read();
L=read();
for(int i=1;i<=n;i++)
a[i]=read(),sum[i]=sum[i-1]+a[i];
solve();
write(f[n]);
return 0;
}
//直接交不能AC哦
//而且此代码与OI-WIKI的略微有些不同
形式3
用于优化形如
f
[
k
]
[
i
]
=
min
1
≤
j
≤
i
(
f
[
k
−
1
]
[
j
−
1
]
+
w
(
j
,
i
)
)
f[k][i]=\min_{1\le j\le i}(f[k-1][j-1]+w(j,i))
f[k][i]=min1≤j≤i(f[k−1][j−1]+w(j,i)) 的转移方程(
w
w
w 满足四边形不等式)
注意到其实跟形式
1
1
1 没有什么区别,因为它不依赖于这一层的值,而是依赖于上一层的值,所以既可以分治也可以二分队列。
据作者喜好(不是作者太菜),例题中只给出分治做法。
例题 CF833B
将一个长度为
n
n
n 的序列分为
k
k
k 段,使得总价值最大。
一段区间的价值表示为区间内不同数字的个数。
n
≤
35000
,
k
≤
50
n\leq 35000,k\leq 50
n≤35000,k≤50
Solution
考虑决策单调性优化DP
令
f
[
i
]
[
j
]
f[i][j]
f[i][j] 表示前
j
j
j 个数分成
i
i
i 段的最小费用,则可得:
f
[
i
]
[
j
]
=
min
1
≤
k
<
j
(
f
[
i
−
1
]
[
k
]
+
w
(
k
+
1
,
j
)
)
f[i][j]=\min_{1\le k<j}(f[i-1][k]+w(k+1,j))
f[i][j]=1≤k<jmin(f[i−1][k]+w(k+1,j))
其中
w
(
l
,
r
)
w(l,r)
w(l,r) 表示 下表为
[
l
,
r
]
[l,r]
[l,r] 中不同数字的个数。
证明
w
w
w 满足决策单调性:
手搓几个样例就可以了口糊过去
证明:
令
g
(
x
,
l
,
r
)
g(x,l,r)
g(x,l,r) 表示
x
x
x 是否在区间
[
l
,
r
]
[l,r]
[l,r] 内出现过,出现为
0
0
0,否则为
1
1
1,
Δ
=
[
C
a
=
=
C
b
+
1
]
\Delta=[C_a==C_{b+1}]
Δ=[Ca==Cb+1]
w
(
a
,
b
+
1
)
+
w
(
a
+
1
,
b
)
=
2
w
(
a
+
1
,
b
)
+
g
(
C
a
,
a
+
1
,
b
)
+
g
(
C
b
+
1
,
a
+
1
,
b
)
−
Δ
w(a,b+1)+w(a+1,b)=2w(a+1,b)+g(C_a,a+1,b)+g(C_{b+1},a+1,b)-\Delta
w(a,b+1)+w(a+1,b)=2w(a+1,b)+g(Ca,a+1,b)+g(Cb+1,a+1,b)−Δ
w
(
a
,
b
)
+
w
(
a
+
1
,
b
+
1
)
=
2
w
(
a
+
1
,
b
)
+
g
(
C
a
,
a
+
1
,
b
)
+
g
(
C
b
+
1
,
a
+
1
,
b
)
w(a,b)+w(a+1,b+1)=2w(a+1,b)+g(C_a,a+1,b)+g(C_{b+1},a+1,b)
w(a,b)+w(a+1,b+1)=2w(a+1,b)+g(Ca,a+1,b)+g(Cb+1,a+1,b)
所以可得:
w
(
a
,
b
+
1
)
+
w
(
a
+
1
,
b
)
≤
w
(
a
,
b
)
+
w
(
a
+
1
,
b
+
1
)
w(a,b+1)+w(a+1,b)\le w(a,b)+w(a+1,b+1)
w(a,b+1)+w(a+1,b)≤w(a,b)+w(a+1,b+1)
因此
w
w
w 满足四边形不等式
所以
f
f
f 满足决策单调性
仅限于分治方法:
接下来就可以 Code了,不过维护
w
(
l
,
r
)
w(l,r)
w(l,r) 时注意可以用莫队的思想,维护双指针,由于分治的特殊性可以保证时间复杂度为
O
(
n
)
O(n)
O(n)
总时间复杂度:
O
(
k
n
log
n
)
O(kn\log n)
O(knlogn)
参考Code:
#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
using namespace std;
const int N=1e5+1,mod=1e9+7;
int n,k,a[N],f[52][N],cnt[N],ans,l,r;
inline void add(int x){
ans+=(++cnt[x]==1);
}
inline void del(int x){
ans-=(--cnt[x]==0);
}
inline int w(int cl,int cr){
while(l<cl)
del(a[l++]);
while(l>cl)
add(a[--l]);
while(r<cr)
add(a[++r]);
while(r>cr)
del(a[r--]);
return ans;
}
void solve(int l,int r,int pl,int pr,int now){
if(l>r)
return ;
int mid=(l+r)>>1,mxp;
int mx=0;
for(int i=pl;i<=min(mid-1,pr);i++){
int o=f[now-1][i]+w(i+1,mid);
if(o>mx)
mx=o,mxp=i;
}
f[now][mid]=max(mx,f[now-1][mid]);
solve(l,mid-1,pl,mxp,now);
solve(mid+1,r,mxp,pr,now);
}
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++)
a[i]=read();
l=1,r=0;
ans=0;
for(int i=1;i<=k;i++){
solve(1,n,0,n,i);
}
cout<<f[k][n]<<"\n";
return 0;
}
//注意不开快读会T哦
形式4
用于优化形如
f
[
i
]
[
j
]
=
min
(
f
[
i
]
[
k
]
+
f
[
k
+
1
]
[
j
]
+
w
(
i
,
j
)
)
f[i][j]=\min(f[i][k]+f[k+1][j]+w(i,j))
f[i][j]=min(f[i][k]+f[k+1][j]+w(i,j)) 的区间DP转移方程
只需要一个简单的操作,就能把这个区间DP的时间复杂度从
O
(
n
3
)
O(n^3)
O(n3) 将为
O
(
n
2
)
O(n^2)
O(n2),就是把枚举
k
k
k 的代码从
for(int k=i;k<j;k++)
改为
for(int k=p[i][j-1];k<=p[i+1][j];k++)
其中
p
[
i
]
[
j
]
p[i][j]
p[i][j] 表示
i
i
i ~
j
j
j的最优分割点。
证明可以参考 《算法竞赛》中的 5.10
和洛谷 石子合并 题解区中 Hurricane、 的题解。
例题

Solution

参考代码:
#include<bits/stdc++.h>
//#define int long long
#define IOS ios::sync_with_stdio(false),cin.tie(NULL),cout.tie(NULL)
using namespace std;
const int N=5e3+1,mod=1e9+7;
int n,a[N],s[N],f[N][N],p[N][N];
inline int read(){
int x=0;
char s=getchar();
while(s<'0'||s>'9')
s=getchar();
while(s>='0'&&s<='9')
x=x*10+s-'0',s=getchar();
return x;
}
signed main(){
// IOS;
n=read();
for(int i=1;i<=n;i++)
a[i]=a[i+n]=read();
for(int i=1;i<=2*n;i++)
s[i]=s[i-1]+a[i],p[i][i]=i;
for(int len=2;len<=n;len++)
for(int l=1;l<=n*2-len+1;l++){
int r=l+len-1;
int res=1e9;
for(int mid=p[l][r-1];mid<=p[l+1][r];mid++)
if(f[l][mid-1]+f[mid+1][r]+s[r]-s[l-1]-a[mid]<res)
res=f[l][mid-1]+f[mid+1][r]+s[r]-s[l-1]-a[mid],p[l][r]=mid;
f[l][r]=res;
}
int ans=1e9;
cout<<f[1][n];
return 0;
}
后话
参考习题单
参考资料:
- OI-WIKI
- 决策单调性优化dp学习笔记
- 关于决策单调性优化动态规划