线性回归是机器学习里面最简单也是最常用的算法,理解了线性回归的推导之后对于后续的学习有很大帮助,所以我决定从这里开始深入学习相关的机器学习模型。
本篇首先从矩阵求导开始切入,然后介绍一次线性回归的推导,再到代码实现。本人也是入门哈,有什么错误望轻喷。
求导
简单求导规则
首先先不管模型本身,对于机器学习来说,各种矩阵的运算非常重要,而求导又是最基础的,所以就放在最前面。(主要参考)
矩阵和标量之间的求导:形状取决于矩阵(矩阵包括向量),无论是标量对矩阵求导,矩阵对标量求导,形状都和矩阵一致,每个元素都是标量求导。
矩阵对矩阵求导:矩阵求导本质上是把向量化为标量的过程,假设存在变量
y
→
m
×
1
\overrightarrow{y}_{m×1}
ym×1和对应的函数
f
(
y
→
)
n
×
1
f(\overrightarrow{y})_{n×1}
f(y)n×1,其中每一行为
f
i
(
y
→
)
f_{i}(\overrightarrow{y})
fi(y),此时存在求导法则:
∂
f
(
y
→
)
∂
y
→
=
(
∂
f
1
(
y
→
)
∂
y
1
⋯
∂
f
1
(
y
→
)
∂
y
m
⋮
⋱
⋮
∂
f
n
(
y
→
)
∂
y
1
⋯
∂
f
n
(
y
→
)
∂
y
m
)
n
×
m
\frac{ \partial f(\overrightarrow{y}) }{ \partial \overrightarrow{y} }=\begin{pmatrix} \frac{ \partial f_{1}(\overrightarrow{y}) }{ \partial {y_1} } & \cdots & \frac{ \partial f_{1}(\overrightarrow{y}) }{ \partial {y_m} }\\ \vdots & \ddots & \vdots\\ \frac{ \partial f_{n}(\overrightarrow{y}) }{ \partial {y_1} } & \cdots & \frac{ \partial f_{n}(\overrightarrow{y}) }{ \partial {y_m} } \end{pmatrix}_{n×m}
∂y∂f(y)=
∂y1∂f1(y)⋮∂y1∂fn(y)⋯⋱⋯∂ym∂f1(y)⋮∂ym∂fn(y)
n×m
在矩阵运算中,由于存在行列的概念,因此需要区别两种布局方式:分子布局和分母布局:
分子布局:分子布局指的是求导后的矩阵行数和分子对应行数相等。
分母布局:分母布局指的是求导后的矩阵行数和分母对应行数相等。
显然,上面的公式为分子布局,因为分子
n
n
n行
(
f
n
×
1
)
(f_{n×1})
(fn×1),最终结果也是
n
n
n行,下面都采用分子布局计算。
下面有两个常用的偏导式,可以用于加速导数计算:
假设存在方阵
A
A
A和向量
y
→
\overrightarrow{y}
y,
- ∂ A y → ∂ y → = A T \frac{ \partial A\overrightarrow{y} }{ \partial \overrightarrow{y} }=A^T ∂y∂Ay=AT
-
∂
y
→
T
A
y
→
∂
y
→
=
A
y
→
+
A
T
y
→
\frac{ \partial \overrightarrow{y}^TA\overrightarrow{y} }{ \partial \overrightarrow{y} }=A\overrightarrow{y}+A^T\overrightarrow{y}
∂y∂yTAy=Ay+ATy(二次型相关),若
A
A
A是对称矩阵,那么可以以进一步化为
2
A
y
→
2A\overrightarrow{y}
2Ay。
简单证明一下1:

这一段证明可能有点抽象,建议可以自己写一下感受一下,我简单说一下我的想法。可以看到,最后对应的每个导数,上面是
f
f
f,下面是
y
y
y,先看第一行,第一行都是对
y
1
y_1
y1求导,从左往右分别是
f
1
f_{1}
f1到
f
m
f_m
fm,因此m对
y
1
y_1
y1的求导从左往右是
∂
f
1
(
y
→
)
∂
y
1
,
∂
f
2
(
y
→
)
∂
y
2
.
.
.
,
∂
f
m
(
y
→
)
∂
y
m
\frac{ \partial f_1(\overrightarrow{y}) }{ \partial {y_1} },\frac{ \partial f_2(\overrightarrow{y}) }{ \partial {y_2} }...,\frac{ \partial f_m(\overrightarrow{y}) }{ \partial {y_m} }
∂y1∂f1(y),∂y2∂f2(y)...,∂ym∂fm(y),这其实就对应了
A
A
A第一列的系数,也就是
a
11
,
a
21
,
.
.
.
,
a
m
1
a_{11},a_{21},...,a_{m1}
a11,a21,...,am1,相当于把列转为了行。
还有一个2我没证过,也可以尝试一下熟悉熟悉规则。
链式求导
对于一般的标量函数
f
(
g
(
x
)
)
f(g(x))
f(g(x)),此时对于
f
(
x
)
f(x)
f(x)和
x
x
x存在链式求导法则:
∂
f
(
g
(
x
)
)
∂
x
=
∂
f
(
x
)
∂
g
(
x
)
∂
g
(
x
)
∂
x
\frac{ \partial f(g(x)) }{ \partial x }=\frac{\partial f(x)}{\partial g(x)}\frac{\partial g(x)}{\partial x}
∂x∂f(g(x))=∂g(x)∂f(x)∂x∂g(x)
但是对于矩阵来说,由于矩阵的乘法一般不满足交换律,此时链式求导法则如下:
∂
f
(
g
(
x
)
)
∂
x
=
∂
g
→
∂
x
→
∂
f
∂
g
→
\frac{ \partial f(g(x)) }{ \partial x }=\frac{\partial \overrightarrow{g}}{\partial \overrightarrow{x}}\frac{\partial f}{\partial \overrightarrow{g}}
∂x∂f(g(x))=∂x∂g∂g∂f
可以看到,大求导在后面,小求导在前面,直接面向自变量的在第一个。
下面给出一个例题,假设存在
x
k
+
1
=
A
x
k
+
B
u
k
x_{k+1}=Ax_k+Bu_{k}
xk+1=Axk+Buk,令
J
=
x
k
+
1
T
x
k
+
1
J=x^T_{k+1}x_{k+1}
J=xk+1Txk+1(J其实是一个控制系统里面的损失函数),计算
∂
J
∂
u
k
\frac{ \partial J }{ \partial u_{k} }
∂uk∂J:

注意其中有一步,也就是
∂
J
∂
x
k
+
1
\frac{ \partial J }{ \partial x_{k+1} }
∂xk+1∂J,这个利用了二次型转换,相当于中间的
A
A
A就是单位阵
I
I
I,
I
I
I是一定对称的,所以结果是
2
x
k
+
1
2x_{k+1}
2xk+1。
线性回归
原理
首先是第一个模型:线性回归。可以先考虑一元线性回归,这个是最简单的回归模型,表达式为
y
=
w
x
+
b
y=wx+b
y=wx+b,需要计算的就是两个参数:
w
,
b
w,b
w,b,
用矩阵计算的相对要复杂一点(但是扩展性强),可以先考虑用标量求导的方式来证明,如下:(参考证明)

这个就计算到了求出导数这一步,没算出解析解,后面代码是用的梯度下降算的。
下面用矩阵的方式求解,这种方法的扩展性比较强(多元线性回归的证明也是这样,本质一样),假设
x
,
y
x,y
x,y均为
n
×
1
n×1
n×1矩阵,假设结果为一列
m
×
1
m×1
m×1向量
t
t
t,前面
m
−
1
m-1
m−1个为
w
w
w,最后一个是
b
b
b,经过证明,其结果为:
t
=
(
x
T
x
)
−
1
y
T
x
t=(x^Tx)^{-1}y^Tx
t=(xTx)−1yTx
下面是简单的证明,这里还是一元一次线性回归的:

最后的
x
T
y
x^Ty
xTy是一个
2
×
1
2×1
2×1向量,导数是
2
×
1
2×1
2×1的,分别对应
w
,
b
w,b
w,b的偏导,当偏导都为0,也就对应了最小值,所以本质还是解方程,解两个偏导方程)。有的证明会把损失函数前面加上
1
/
2
n
1/2n
1/2n,也就是除掉样本数,但本质其实是一样的,不影响求解。
我一开始其实写错了,上面打叉的就是第一次写错的,还是后面写代码的时候才发现的(所以动手实践一下还是很重要的)。
注意:损失函数本身是一个标量(
1
×
1
1×1
1×1),其导数是
2
×
1
2×1
2×1的,对应了求解的参数矩阵。
代码
一元一次线性回归
首先是基于解方程的思路,也就是直接算出数值解(对应于上面基于矩阵的证明部分)。
def my_lr(x,y):
n = x.shape[0]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
# print(x.shape) # (n,2)
t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
w,b=t[0][0],t[1][0]
# 下面进行拟合
y_hat = w*x[:,0]+b # 取第一列,第二列是增广的
return y_hat
上面的本质在解方程,下面用梯度下降的思路求解:
简单概括梯度下降就是:
w
=
w
−
α
▽
w=w-α▽
w=w−α▽,其中
▽
▽
▽是梯度(多元情况的导数),
▽
=
∂
J
∂
w
▽=\frac{ \partial J}{ \partial w }
▽=∂w∂J,
α
α
α是学习率。
首先是基于标量方式求解各个变量的,也就是用
w
,
b
w,b
w,b这样的形式写出来,然后求梯度迭代:
def my_gradi_lr(x,y):
print('--------------基于标量的梯度下降--------------')
# 定义损失函数:T(w,b)=1/(2m)*∑(yi_hat-yi),yi_hat=wxi-b
# w=w-α(1/m*∑xi(yi_hat-yi)) b=b-α(1/m*∑(yi_hat-yi))
m = x.shape[0]
w,b=0,0
alpha=0.01
epochs=50
for i in range(epochs):
y_hat = w*x+b # 计算拟合值
w=(w-alpha*(x.T@(y_hat-y))/m)# ∑xi(yi_hat-yi)/m
b=(b-alpha*(np.sum(y_hat-y))/m) # ∑(yi_hat-yi)/m
y_hat = w * x + b # 更新新y_hat计算loss
loss = 1/(2*m)*(y_hat-y).T@(y_hat-y) # 1/(2m)*∑(yi_hat-yi)
print('epoch:%d loss:%.4f'%(i+1,loss))
# print(w,b)
return w*x+b
推导的过程就是链式求导,因为是完全标量的,还是比较简单的。
下面是基于矩阵的,推导过程跟前面矩阵求解里面是一致的,如果一定要比较的话,上面那种标量直观一点,但是参数多了就不方便了,下面的适合更多参数,比如之后应该会提到的多元线性回归。
def my_mat_gradi_lr(x,y):
print('--------------基于矩阵的梯度下降--------------')
n = x.shape[0]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
alpha=0.01
epochs=50
t=np.zeros((2,1)) # 系数矩阵
for i in range(epochs):
gradi = 2*(x.T@x@t-x.T@y)/(2*n)
t=t - alpha * gradi
loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
print('epoch:%d loss:%.4f' % (i + 1, loss))
return x@t # y_hat
这两种是完全一样的,具体可以看迭代的过程,loss的变化是一模一样的。
下面是运算的结果,sklearn(sklearn model)的可以视为标答,数值解(my model)的答案是和sklearn的是一样的,说明结果是对的。两个grendient都是对应的梯度下降的解法,两种迭代的算法是一样的,从迭代过程中的loss可以看出(可以运行一下代码),由于迭代次数次数比较少(50),所以和精确解还是有一定距离。
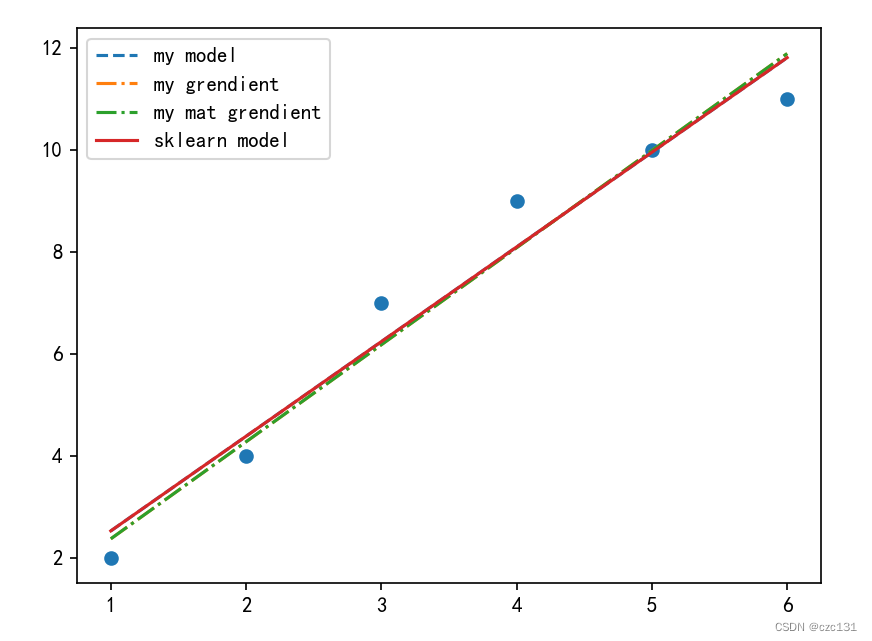
下面是代码:
# 一元一次线性回归
import numpy as np
from matplotlib import pyplot as plt
from numpy import dot
from numpy.linalg import inv
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def my_lr(x,y):
n = x.shape[0]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
# print(x.shape)
t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
# print(t.shape)
# print(t)
w,b=t[0][0],t[1][0]
# print(w,b)
# 下面进行拟合
y_hat = w*x[:,0]+b # 取第一列,第二列是增广的
return y_hat
def skle_lr(x,y):
model = LinearRegression()
model.fit(x, y)
return model.predict(x)
# 利用梯度下降求解(基于标量链式求导)
def my_gradi_lr(x,y):
print('--------------基于标量的梯度下降--------------')
# 定义损失函数:T(w,b)=1/(2m)*∑(yi_hat-yi),yi_hat=wxi-b
# w=w-α(1/m*∑xi(yi_hat-yi)) b=b-α(1/m*∑(yi_hat-yi))
m = x.shape[0]
w,b=0,0
alpha=0.01
epochs=50
for i in range(epochs):
# print('epoch:',i+1)
y_hat = w*x+b # 计算拟合值
w=(w-alpha*(x.T@(y_hat-y))/m)# ∑xi(yi_hat-yi)/m
b=(b-alpha*(np.sum(y_hat-y))/m) # ∑(yi_hat-yi)/m
y_hat = w * x + b # 更新新y_hat计算loss
loss = 1/(2*m)*(y_hat-y).T@(y_hat-y) # 1/(2m)*∑(yi_hat-yi)
print('epoch:%d loss:%.4f'%(i+1,loss))
# print(w,b)
return w*x+b
# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
print('--------------基于矩阵的梯度下降--------------')
n = x.shape[0]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
alpha=0.01
epochs=50
t=np.zeros((2,1)) # 系数矩阵
for i in range(epochs):
# print(x.T.shape)
# print(t.shape)
# print((x.T@x@t).shape)
gradi = 2*(x.T@x@t-x.T@y)/(2*n)
t=t - alpha * gradi
loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
print('epoch:%d loss:%.4f' % (i + 1, loss))
return x@t # y_hat
if __name__ == '__main__':
x=np.array([1,2,3,4,5,6]).reshape(-1,1)
y=np.array([2,4,7,9,10,11]).reshape(-1,1) # 列向量
my_y_hat = my_lr(x,y)
skle_y_hat = skle_lr(x,y)
my_gradi_y_hat = my_gradi_lr(x,y)
my_mat_gradi_y_hat = my_mat_gradi_lr(x,y)
plt.scatter(x,y)
plt.plot(x,my_y_hat,linestyle='--',label='my model')
plt.plot(x,my_gradi_y_hat,linestyle='-.',label='my grendient')
plt.plot(x,my_mat_gradi_y_hat,linestyle='-.',label='my mat grendient')
plt.plot(x,skle_y_hat,linestyle='-',label='sklearn model')
plt.legend()
plt.show()
多元一次线性回归
对于多元线性回归,其实本质上还是一样的,下面提供多元线性回归的代码,使用的例子是一个三元一次线性回归。具体的证明和上面矩阵证明的过程是完全一致的,解析求解的方式(求逆)的代码和一元的一样,用梯度下降方式的就改一点点就可以(其实一元也就是特殊的多元,下面这段代码也可以用)。
# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
print('--------------基于矩阵的梯度下降--------------')
n = x.shape[0]
n_samples = x.shape[1]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
alpha=0.01
epochs=50
t=np.zeros((n_samples+1,1)) # 系数矩阵,唯一变化的地方
for i in range(epochs):
gradi = 2*(x.T@x@t-x.T@y)/(2*n)
t=t - alpha * gradi
loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
print('epoch:%d loss:%.4f' % (i + 1, loss))
return x@t # y_hat
这里因为不方便画出图像,就画出y的比较了,每个点都是实际点,线对应的都是拟合值,x轴表示第几个点。
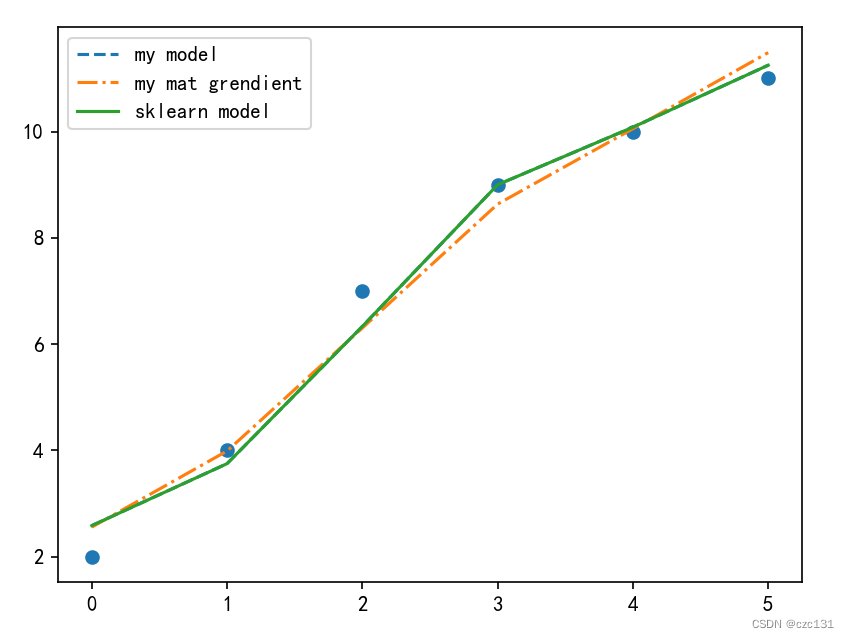
从结果中看解析解和sklearn得到是一样的,就是精确解,梯度下降还是差的比较多,是因为迭代次数少(50),提高到5000或者改变学习率(alpha)就可以得到更好的结果。
贴出代码:
# 多元线性回归
import numpy as np
from matplotlib import pyplot as plt
from numpy import dot
from numpy.linalg import inv
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def my_lr(x,y):
n = x.shape[0]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
# print(x.shape)
t = (inv(dot(x.T,x))@x.T@y) # t=(xx^T)^(-1)y^Tx, @表示矩阵乘法,dot也是矩阵乘法
# 下面进行拟合
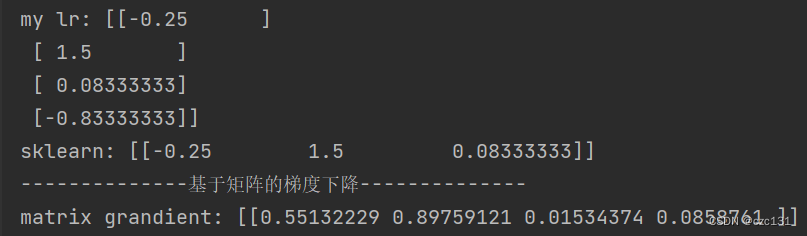
print('my lr:',t)
return x@t
def skle_lr(x,y):
model = LinearRegression()
model.fit(x, y)
print('sklearn:',model.coef_)
return model.predict(x)
# 采用矩阵形式的梯度下降
def my_mat_gradi_lr(x,y):
print('--------------基于矩阵的梯度下降--------------')
n = x.shape[0]
n_samples = x.shape[1]
x = np.hstack((x,np.ones((n,1)))) # 加上一列n
alpha=0.01
epochs=50
t=np.zeros((n_samples+1,1)) # 系数矩阵
for i in range(epochs):
gradi = 2*(x.T@x@t-x.T@y)/(2*n)
t=t - alpha * gradi
loss = (t.T@x.T@x@t+y.T@y-2*y.T@x@t)/(2*n)
# print('epoch:%d loss:%.4f' % (i + 1, loss))
print('matrix grandient:',t.T)
return x@t # y_hat
if __name__ == '__main__':
x=np.array([[1,2,3,4,5,6],[2,3,5,7,8,9],[8,7,5,4,2,1]]).T
y=np.array([2,4,7,9,10,11]).reshape(-1,1) # 列向量
my_y_hat = my_lr(x,y)
skle_y_hat = skle_lr(x,y)
my_mat_gradi_y_hat = my_mat_gradi_lr(x,y)
plot_x = np.arange(y.shape[0])
plt.scatter(plot_x,y)
plt.plot(plot_x,my_y_hat,linestyle='--',label='my model')
plt.plot(plot_x,my_mat_gradi_y_hat,linestyle='-.',label='my mat grendient')
plt.plot(plot_x,skle_y_hat,linestyle='-',label='sklearn model')
plt.legend()
plt.show()
❀❀❀完结撒花❀❀❀

![【YOLOv8改进[Neck]】使用BiFPN助力V8更优秀](https://img-blog.csdnimg.cn/direct/7462a827f58b4462b2a2c1196c550107.png)