数值分析（三） Lagrange（拉格朗日）插值法及Matlab代码实现

前言
一、Lagrange（拉格朗日）插值
- 1. 线性插值
- 2. 抛物插值
- 3. 拉格朗日插值多项式
二、Lagrange插值算法及matlab代码
- 1. Lagrange 插值算法matlab实现
- 2 实例
- 3. 线性插值示意图代码
- 4. 抛物插值示意图代码
三、总结
四、插值法专栏

前言

本篇为插值法专栏第三篇内容讲述，此章主要讲述 Lagrange（拉格朗日）插值法及matlab代码，其中也给出详细的例子让大家更好的理解Lagrange插值法
提示 之前已经介绍牛顿插值法和三次样条插值，如果没看过前两篇的可以点击以下链接阅读

数值分析（一）牛顿插值法
数值分析（二）三次样条插值法
数值分析（二续）三次样条插值二类边界完整matlab代码
数值分析（三） Lagrange（拉格朗日）插值法及Matlab代码实现
数值分析（四） Hermite（埃尔米特）插值法及matlab代码

一、Lagrange（拉格朗日）插值

为了构造满足插值条件 $p(x_i) = f(x_i), (i=0, 1, 2, \dots, n)$ 的便于使用的插值多项式 $P (x)$ ，在介绍Lagrange插值前先补充一下 线性插值 和 抛物插值 的知识点。

1. 线性插值

线性插值是代数插值的最简单形式。假设给定了函数 $f (x)$ 在两个互异的点的值， $x_0, x_1, y_0 = f(x_0), y_1 = f(x_1)$ ，现要求用线性函数 $p (x) = a x + b$ 近似的代替 $f (x)$ 。选择参数 $a$ 和 $b$ , 使 $p(x_i) = f(x_i), (i=0, 1)$ 。称这样的线性函数 $P (x)$ 为 $f (x)$ 的线性插值函数。
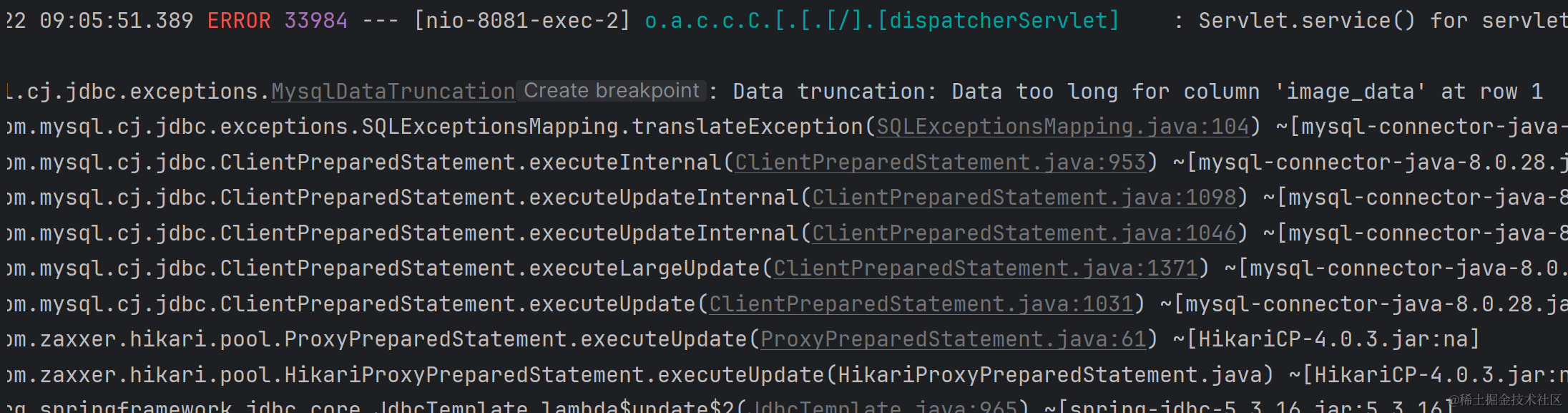
线性插值的几何意义：用通过点 $A(x_0, f(x_0))$ 和 $B(x_1, f(x_1))$ 的直线近似地代替曲线 $y = f (x)$ 由解析几何知道，这条直线用点斜式表示为（如下图所示）: ${y_0} + \frac{{{y_1} - {y_0}}}{{{x_1} - {x_0}}}(x - {x_0}) \to p(x) = \frac{{x - {x_1}}}{{{x_0} - {x_1}}}{y_0} + \frac{{x - {x_0}}}{{{x_1} - {x_0}}}{y_1}$
在这里插入图片描述

为了便于推广，那么记 $l_0(x) = \frac{x-x_1}{x_0-x_1}, l_1(x) = \frac{x-x_0}{x_1-x_0}$ 这是一次函数，具有如下性质 $\begin{matrix} l_0(x_0)=1, & l_0(x_1)=0, \\ l_1(x_0) = 0 & l_1(x_1) = 1\end{matrix} \\ l_0(x)+l_1(x) =1$
那么可以记为： $l_k(x_i) = \delta_{ki}= \left\{\begin{matrix} 1 & (i=k)\\0 &(i \ne k) &\end{matrix}\right.$ 那么 $l_0(x)$ 和 $l_1(x)$ 称为线性插值基函数，且有 $l_k(x) = \prod_{j=0,j \ne k}^{1}\frac{x-x_j}{x_k-x_j}, (k=0,1)$ 则上述线性插值函数可以表示为与基函数的线性组合 $p(x) = l_0(x)y_0 + l_1(x)y_1$

2. 抛物插值

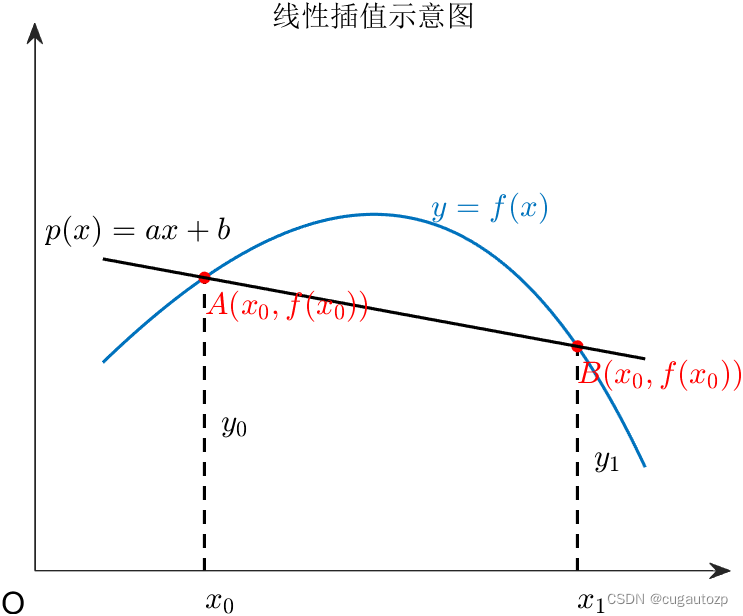
抛物插值又称二次插值，它也是常用的代数插值之一。设已知 $f (x)$ 在三个互异点 $x_0, x_1, x_2$ 的函数值 $y_0, y_1, y_2$ ，要构造次数不超过二次的多项式
$P(x) = a_2x^2 + a_1x + a_0$ 使满足二次插值条件： $P(x_i) = y_i (i=0,1,2)$ 这就是二次插值问题。其几何意义是用经过3个点 $x{}_0,{y_0}),(x{}_1,{y_1}),(x{}_2,{y_2})$ 的抛物线 $y = P (x)$ 近似代替曲线 $y = f (x)$ , 如下图所示。因此也称之为抛物插值。

在这里插入图片描述

线性插值 和 抛物插值 两个示意图使用matlab绘制，并借助使用了 slandarer 大佬的一个绘制带箭头的坐标轴工具箱，代码将在下方给出

其中 $P (x)$ 的参数 $a_0,a_1,a_2$ 直接由插值条件决定，即 $a_0,a_1,a_2$ 满足下面的代数方程组： $\left\{ \begin{array}{l} {a_0} + {a_1}{x_0} + {a_2}x_0^2 = {y_0}\\ {a_0} + {a_1}{x_1} + {a_2}x_1^2 = {y_1}\\ {a_0} + {a_1}{x_2} + {a_2}x_2^2 = {y_2} \end{array} \right.$ 那么其系数矩阵为： $\left[ {\begin{matrix} 1&{{x_0}}&{x_0^2}\\ 1&{{x_1}}&{x_1^2}\\ 1&{{x_2}}&{x_2^2} \end{matrix}} \right]$ 此行列式是范德蒙行列式，当 $x_0 \ne x_1 \ne x_2$ 时，方程组的解唯一，为了与下一节的Lagrange插值公式比较,仿线性插值,用基函数的方法求解方程组，求二次式 $l_0(x)$ ，使其满足条件： $l_0(x_0)=1, l_0(x_1)=0,l_0(x_2)=0$ ，于是可以知道 $x_1,x_2$ 是 $l_0(x)$ 的两个零点，则 ${l_0}(x) = c(x - {x_1})(x - {x_2})$ 再由另一个条件 $l_0(x_0)=1$ 解得系数为 $\frac{1}{{({x_0} - {x_1})({x_0} - {x_2})}}$ 从而导出 ${l_0}(x) = \frac{{(x - {x_1})(x - {x_2})}}{{({x_0} - {x_1})({x_0} - {x_2})}}$ 类似地可以构造出满足条件： $l_0(x_0)=0, l_0(x_1)=1,l_0(x_2)=0$ 的插值多项式 ${l_1}(x) = \frac{{(x - {x_0})(x - {x_2})}}{{({x_1} - {x_0})({x_1} - {x_2})}}$ 以及满足条件 $l_0(x_0)=0, l_0(x_1)=0,l_0(x_2)=1$ 的插值多项式 ${l_2}(x) = \frac{{(x - {x_0})(x - {x_1})}}{{({x_2} - {x_0})({x_2} - {x_1})}}$ 这样构造出来的 $l_0(x), l_0(x),l_0(x)$ 称为抛物插值的基函数，取已知数据 ${y_0},{y_1},{y_2}$ 作为线性组合系数，将基函数 ${l_0}(x),{l_1}(x),{l_2}(x)$ 线性组合可得 $\frac{{(x - {x_1})(x - {x_2})}}{{({x_0} - {x_1})({x_0} - {x_2})}}{y_0} + \frac{{(x - {x_0})(x - {x_2})}}{{({x_1} - {x_0})({x_1} - {x_2})}}{y_1} + \frac{{(x - {x_0})(x - {x_1})}}{{({x_2} - {x_0})({x_2} - {x_1})}}{y_2}$ 容易看出， $P (x)$ 满足条件 $P(x_i)=y_i (i=0,1,2)$

3. 拉格朗日插值多项式

通过上述描述可以发现，两个插值点可求出一次插值多项式，而三个插值点可求出二次插值多项式。插值点增加到 $n + 1$ 个时，也就是通过 $n + 1$ 个不同的已知点 $({x_i},{y_i})(i = 0,1, \cdots ,n)$ ，来构造一个次数为n的代数多项式 $P (x)$ 。与推导抛物插值的基函数类似，先构造一个特殊 $n$ 次多项式 $l_i(x)$ 的插值问题，使其在各节点 $x_i$ 上满足 ${l_k}({x_0}) = 0, \cdots ,{l_k}({x_{k - 1}}) = 0,{l_k}({x_k}) = 1,{l_k}({x_{k + 1}}) = 0, \cdots ,{l_k}({x_n}) = 0$ 即 $l_k(x_i)=\delta _{ki}=\left\{\begin{matrix} 1 & (i=k)\\ 0 & (i\ne k) \end{matrix}\right.$ 由条件 ${l_k}({x_i}) = 0,(i \ne k)$ 可知， ${x_0},{x_1}, \cdots ,{x_{k - 1}},{x_{k + 1}}, \cdots ,{x_n}$ 都是 $n$ 次 ${l_k}(x)$ 的零点，故可设 ${l_k}(x) = {A_k}(x - {x_0})(x - {x_1}) \cdots (x - {x_{k - 1}})(x - {x_{k + 1}}) \cdots (x - {x_n})$ 其中 $A_k$ 为待定常数。有条件 ${l_k}({x_k}) = 1$ ，可求得 ${A_k}$ 为： ${A_k}\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})} = 1$ 于是 ${A_k} = \frac{1}{\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})}}$ 代入上式，得 $l_k(x) = \frac{\prod_{j = 0,j \ne k}^n {({x} - {x_j})}}{\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})}} = \prod_{j = 0,j \ne k}^n \frac{{x} - {x_j}}{{x_k} - {x_j}}$ 称 ${l_k}(x)$ 为关于基点 $x_i$ 的 $n$ 次插值基函数 $(i=0,1,\cdots,n)$ ，那么以 $n + 1$ 个 $n$ 次基本插值多项式 ${l_k}(x)(k = 0,1, \cdots ,n)$ 为基础,就能直接写出满足插值条件 $P(x_i)=f(x_i)(i=0,1,2,\cdots,n)$ 的 $n$ 次代数插值多项式 ${l_0}(x){y_0} + {l_1}(x){y_1} + \cdots + {l_n}(x){y_n}$ 其中每个插值基函数 ${l_k}(x)(k = 0,1, \cdots ,n)$ 都是 $n$ 次值多项式,所以他们的线性组合 $\sum\limits_{k = 0}^n {{l_k}(x){y_k}}$
即为 $n$ 次拉格朗日插值多项式，并记作 $L_n(x)$ ，引入 $\omega_{n+1}(x)$ 为 ${\omega _{n + 1}}(x) = (x - {x_0})(x - {x_1}) \cdots (x - {x_n}){\rm{ }}$ 那么得到 ${{\omega '}_{n + 1}}({x_k}) = ({x_k} - {x_0}) \cdots ({x_k} - {x_{k - 1}})({x_k} - {x_{k + 1}}) \cdots ({x_k} - {x_n})$ 那么 $L_n(x)$ 可以转化为 ${L_n}(x) = {\rm{ }}\sum\limits_{k = 0}^n {{y_k}\frac{{{\omega _{n + 1}}(x)}}{{(x - {x_k}){{\omega '}_{n + 1}}({x_k})}}}$

二、Lagrange插值算法及matlab代码

Matlab 版本号 2022b
根据Lagrange 插值算法构建 lagrange.m文件
为了让代码具有可输出性，让大家通俗易懂，编写了一个lab函数，并构建了lab.m文件

1. Lagrange 插值算法matlab实现

下面展示拉格朗日插值函数代码: lagrange.m（复制代码，保存此名称）

function varargout = lagrange(x0,y0,varargin)
% x0 为节点
% y0 为节点对应的函数值
% x 为插值点
m = length(x0);
L1 = zeros(m,m);
l = [];

% step 1 构造基函数lk
for k = 1 : m
    V = 1;
    for i = 1 : m
        if k ~= i
            V = conv(V,poly(x0(i))) / (x0(k) - x0(i));
        end
    end
    L1(k,:) = V;
    l = cat(1,l,poly2sym(V));
end
fprintf('基函数为：\n');

for k = 1:m
    fprintf(['l',lab(k),'(x)=%s\n'],l(k));fprintf('\n');
end

% 通过矩阵乘积求L(x)
L = y0 * l;
L1 = str2sym(['P(x)=',char(L)]);
disp(L1)
% L = simplify(L1);
S = ['$',latex(L1),'$'];
fprintf('拉格朗日多项式为:\nP(x)=%s\n',L);fprintf('\n');
% symdisp(L)
L = matlabFunction(L);
if nargin == 3
    varargout{1} = feval(L,varargin{1});
    plot(x0,y0,'bo')
    hold on
    plot(varargin{1},varargout{1},'rp')
    plot(min([varargin{1},x0]):0.01:max([varargin{1},x0]),feval(L,min([varargin{1},x0]):0.01:max([varargin{1},x0])),'k-','LineWidth',1)
    subtitle(S,'Interpreter','latex','FontSize',14)
    title('Lagrange插值','FontSize',14)
    legend('原始点','插值点','插值函数P(x)')
else
plot(x0,y0,'bo')
hold on
plot(min(x0):0.01:max(x0),feval(L,min(x0):0.01:max(x0)),'k-','LineWidth',1)
subtitle(S,'Interpreter','latex','FontSize',14)
title('Lagrange插值','FontSize',14)
legend('原始点','插值函数P(x)')
end
end

下面展示lab代码: lab.m（复制代码，保存此名称）

function label = lab(k)
name = {'₀','₁','₂','₃','₄','₅','₆','₇','₈','₉'};
label = '';
k=k-1;
if k == 0
    label = name{k+1};
else
    while 1
        if mod(k,10)==0 && floor(k/10)==0
            break
        end
        j = mod(k,10);
        k = floor(k/10);
        label = cat(2,name{j+1},label);
    end
end
end

2 实例

话不多说，直接讲述lagrange函数使用说明

1. lagrange(x0,y0)：输入参数只有2个时，x0 为节点，y0 为节点对应的函数值；自动输出：基函数，拉格朗日多项式，插值函数图像
2. y = lagrange(x0,y0,x)：输入参数为3个时，x0 为节点，y0 为节点对应的函数值，x 为插值点；输出：y为插值点对应函数值，自动输出：基函数，拉格朗日多项式，插值函数图像

示例展示一下：
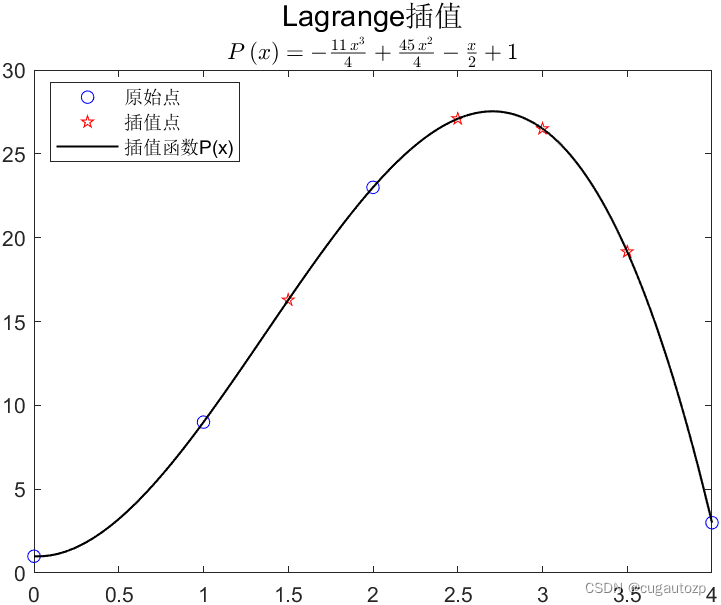
已知 $f (x)$ 的观测数据为如下表所示，并构造Lagrange插值多项式

$x$	0	1	2	4
$f (x)$	1	9	23	3

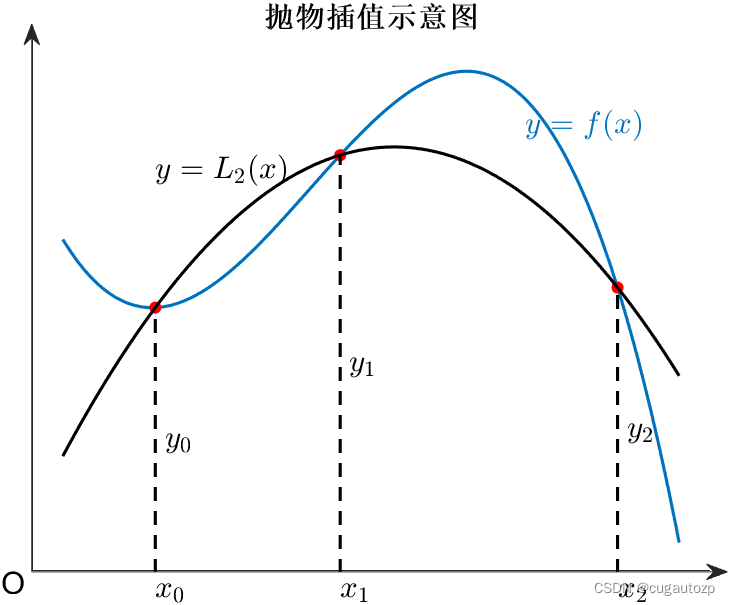
手动计算一下，四个点可构造三次Lagrange插值多项式，其基函数为：
${l_0}(x) = \frac{{(x - 1)(x - 2)(x - 4)}}{{(0 - 1)(0 - 2)(0 - 4)}} = - \frac{1}{8}{x^3} + \frac{7}{8}{x^2} - \frac{7}{4}x + 1$ ${l_1}(x) = \frac{{(x - 0)(x - 2)(x - 4)}}{{(1 - 0)(1 - 2)(1 - 4)}} = \frac{1}{3}{x^3} - 2{x^2} + \frac{8}{3}x$ ${l_2}(x) = \frac{{(x - 0)(x - 1)(x - 4)}}{{(2 - 0)(2 - 1)(2 - 4)}} = - \frac{1}{4}{x^3} + \frac{5}{4}{x^2} - x$ ${l_3}(x) = \frac{{(x - 0)(x - 1)(x - 2)}}{{(4 - 0)(4 - 1)(4 - 2)}} = \frac{1}{{24}}{x^3} - \frac{1}{8}{x^2} + \frac{1}{{12}}x$ 那么Lagrange插值多项式为： $\begin{array}{c} {L_3}(x) = \sum\limits_{k = 0}^3 {{y_k}} {l_k}(x) = {l_0}(x) + 9{l_1}(x) + 23{l_2}(x) + 3{l_3}(x) = - \frac{{11}}{4}{x^3} + \frac{{45}}{4}{x^2} - \frac{1}{2}x + 1 \end{array}$

接下来利用上述lagrange(x0,y0)，检验一下，先构建一个叫demo.m文件，接下来复制此代码放入其中，切记要将demo.m`文件、lagrange.m文件和lab.m文件放在一个文件内（新手注意！！！）

x0 = [0 1 2 4];
y0 = [1 9 23 3];
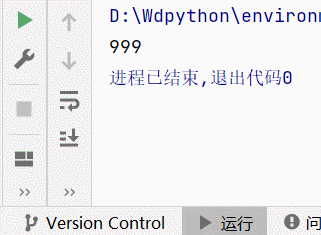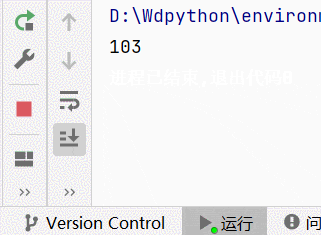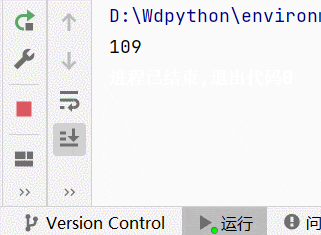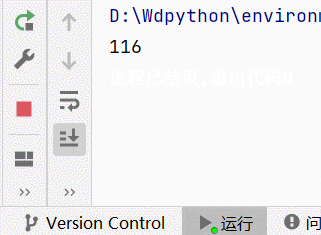
lagrange(x0,y0);

直接启动运行，输出结果如下，发现和手动计算结果一摸一样
在这里插入图片描述
这里代码中还给出了此插值函数的图像

在上述的基础上需要求出当 $x={1.5, 2.5, 3, 3.5}$ 时，对应的函数值是什么？复制如下代码直接运行看看结果。

x0 = [0 1 2 4];
y0 = [1 9 23 3];
x = [1.5 2.5 3 3.5];
y = lagrange(x0,y0,x)

输出函数值为：
在这里插入图片描述

3. 线性插值示意图代码

注意：一定需要有坐标轴工具箱函数否则会报错，请前往上述链接下载。

% 使用了CSDN: Slandarer大佬开源的带箭头的坐标函数包
% 剩余代码由本人撰写
% 此代码为CSDN文章中线性插值示意图代码
% @Author
% Copyright© 2024.3.12
% CSDN name: cugautozp
% GitHub: https://github.com/cug-auto-zp
clc
clear
close all
x=0.2:0.01:1.8;
y=x-exp(x-1);
plot(x,y,'LineWidth',1.5)
% 修改坐标轴属性
ax=gca;
ax.XLim = [0,2];
ax.YLim = [-0.6,0.3];
ax.YTick = [];
ax.XTick = [];
arrowAxes(ax)


x0 = [0.5,1.6];
y0 = x0-exp(x0-1);
hold on
for i=1:length(x0)
    plot(x0(i)*[1,1],[-0.6,y0(i)],'LineStyle','--','LineWidth',1.5,'Color',[0,0,0])
    text(x0(i)+0.05,(-0.6+y0(i))/2,['$y_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
    text(x0(i),-0.65,['$x_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
end
plot(x0,y0,'LineStyle','none','Marker','.','MarkerSize',20,'Color',[1,0,0])
t=polyfit(x0,y0,1);
plot(x,polyval(t,x),'-k','LineWidth',1.5)
text(1,0.1,'$y = f(x)$','Interpreter','latex','FontSize',15,'Color',[0.00,0.45,0.74])
text(0.1,0,'$p(x)=ax+b$','Interpreter','latex','FontSize',15,'Color',[0,0,0])
text(x0(1),y0(1)-0.05,'$A(x_0,f(x_0))$','Interpreter','latex','FontSize',15,'Color',[1,0,0])
text(x0(2),y0(2)-0.05,'$B(x_0,f(x_0))$','Interpreter','latex','FontSize',15,'Color',[1,0,0])
title('线性插值示意图','FontSize',14)
text(-0.1,-0.65,'O','FontSize',15,'Color',[0,0,0])

4. 抛物插值示意图代码

% 使用了CSDN: Slandarer大佬开源的带箭头的坐标函数包
% 剩余代码由本人撰写
% 此代码为CSDN文章中抛物插值示意图代码
% @Author
% Copyright© 2024.3.12
% CSDN name: cugautozp
% GitHub: https://github.com/cug-auto-zp

clc
clear
close all
x=0:0.1:20;
y=-0.5*(x-4).^3+15*(x-4)+6*(x-4).^2+5;
plot(x,y,'LineWidth',1.5)


ax=gca;
ax.XLim = [-1,21];
ax.YLim = [-300,300];
ax.YTick = [];
ax.XTick = [];
arrowAxes(ax)


x0 = [3,9,18];
y0 = -0.5*(x0-4).^3+15*(x0-4)+6*(x0-4).^2+5;
hold on
plot(x0,y0,'LineStyle','none','Marker','.','MarkerSize',20,'Color',[1,0,0])
text(-2,-310,'O','FontSize',15,'Color',[0,0,0])
for i=1:length(x0)
    plot(x0(i)*[1,1],[-300,y0(i)],'LineStyle','--','LineWidth',1.5,'Color',[0,0,0])
    text(x0(i)+0.3,(-300+y0(i))/2,['$y_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
    text(x0(i),-320,['$x_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
end
t=polyfit(x0,y0,2);
plot(x,polyval(t,x),'-k','LineWidth',1.5)
text(15,200,'$y = f(x)$','Interpreter','latex','FontSize',15,'Color',[0.00,0.45,0.74])
text(3,150,'$y = L_2(x)$','Interpreter','latex','FontSize',15,'Color',[0,0,0])
title('抛物插值示意图')