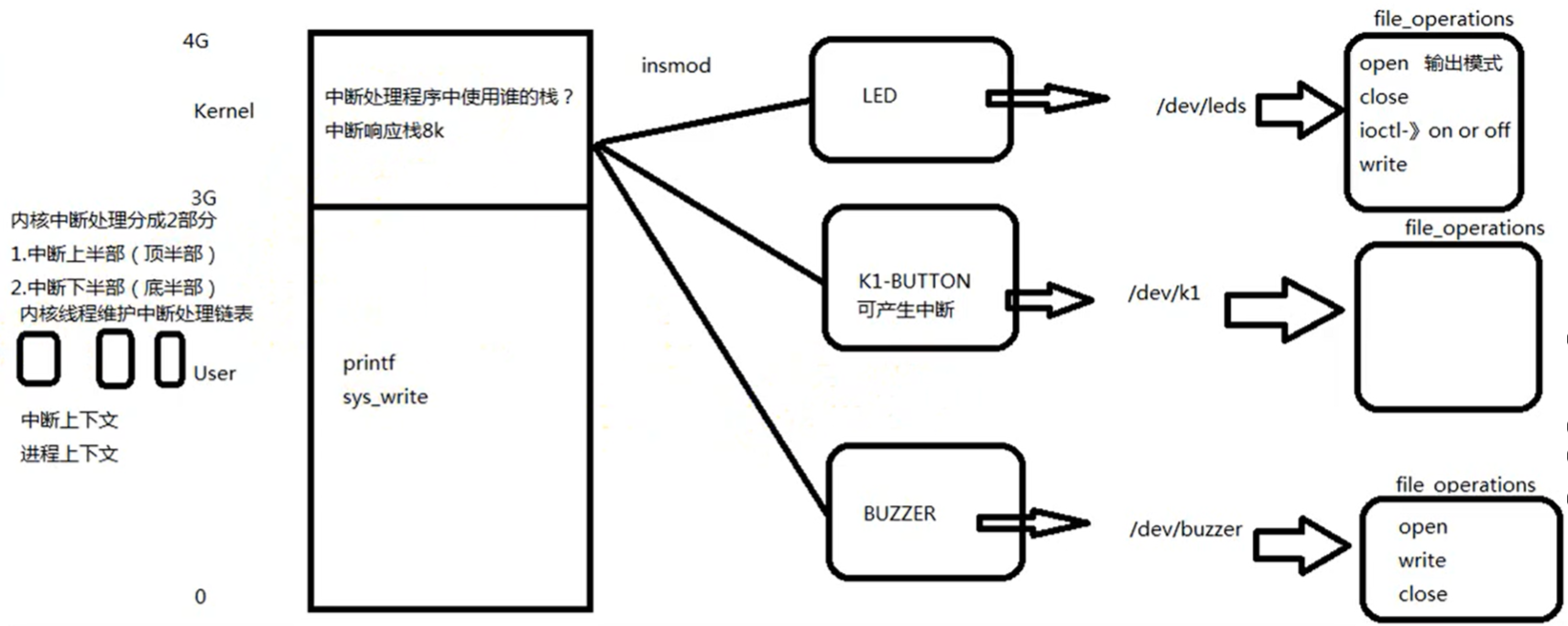
1 十进制展开数
十进制展开数(Decimal Expansion Number)的计算公式:
DEN = n^3 - n - 1
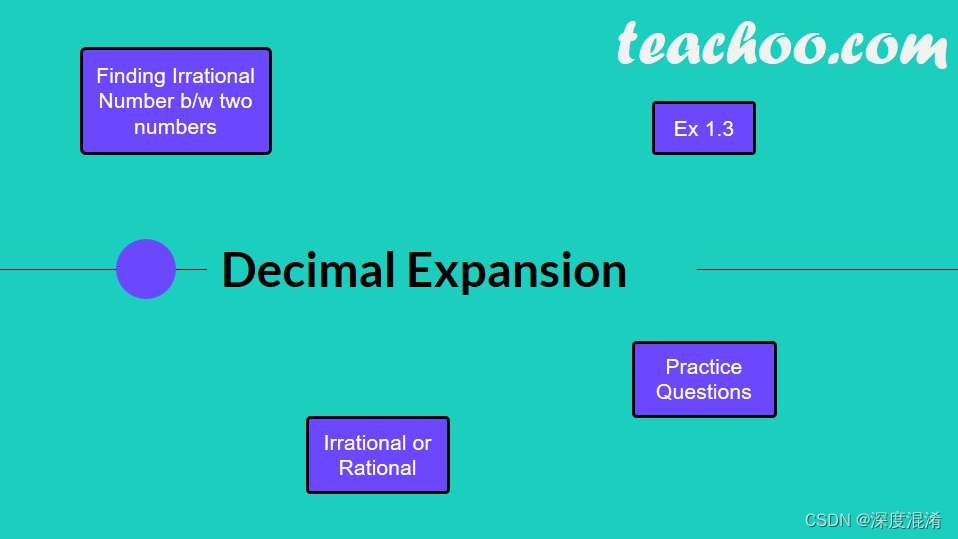
The decimal expansion of a number is its representation in base -10 (i.e., in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the s place.
2 计算结果
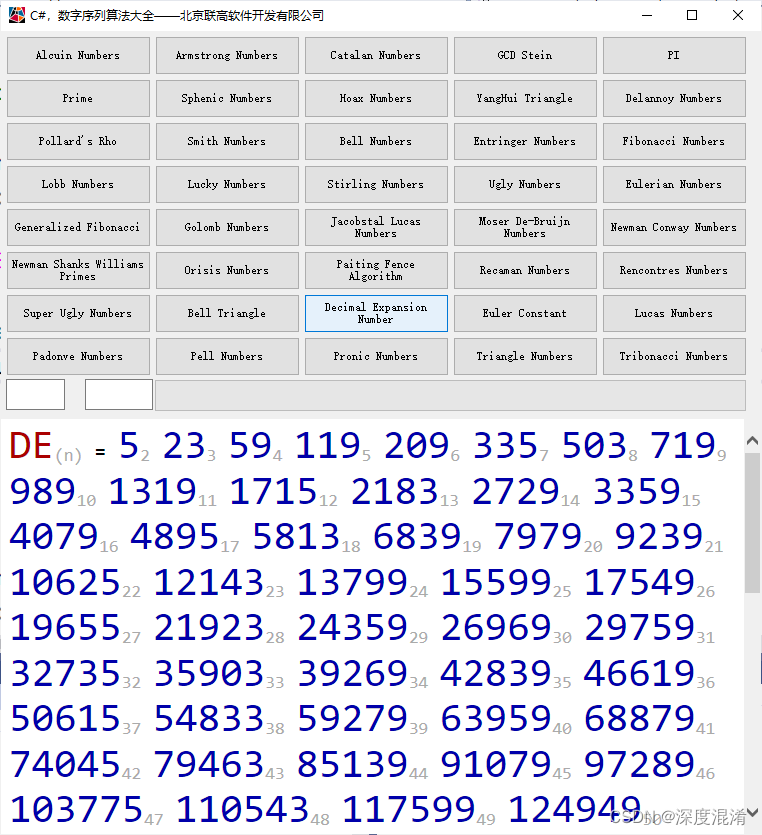
3 源程序
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
public static int Decimal_Expansion_Number(int n)
{
return n * n * n - n - 1;
}
}
}
The decimal expansion of a number is its representation in base-10 (i.e., in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of 10, decreasing from left to right, and with a decimal place indicating the s place. For example, the number with decimal expansion 1234.56 is defined as
Expressions written in this form (where negative are allowed as exemplified above but usually not considered in elementary education contexts) are said to be in expanded notation.
Other examples include the decimal expansion of given by 625, of given by 3.14159..., and of given by 0.1111.... The decimal expansion of a number can be found in the Wolfram Language using the command RealDigits[n], or equivalently, RealDigits[n, 10].
The decimal expansion of a number may terminate (in which case the number is called a regular number or finite decimal, e.g., ), eventually become periodic (in which case the number is called a repeating decimal, e.g., ), or continue infinitely without repeating (in which case the number is called irrational).
The following table summarizes the decimal expansions of the first few unit fractions. As usual, the repeating portion of a decimal expansion is conventionally denoted with a vinculum.
4 代码格式
using System;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
public static int Decimal_Expansion_Number(int n)
{
return n * n * n - n - 1;
}
}
}







![[leetcode] 32. 最长有效括号](https://img-blog.csdnimg.cn/direct/a36c1b59f2eb48eebd27dc7ba26116ca.png)
![[Java][算法 哈希]Day 01---LeetCode 热题 100---01~03](https://img-blog.csdnimg.cn/direct/328ebc11a97342e0a853a61931fa8c22.png)