0x53 区间DP

到目前为止，我们介绍的线性DP一般从初态开始，沿着阶段的扩张向某个方向递推，直至计算出目标状态。区间DP也属于线性DP中的一种，它以“区间长度”作为DP的“阶段”，使用两个坐标（区间的左右端点）描述每个维度。在区间DP中，一个状态由若干个比它更小且包含于它的区间所代表的状态转移而来，因此区间DP的决策往往就是划分区间的方法。区间DP的初态一般就由长度为1的“元区间”构成。这种向下划分、再向上递推的模式与某些树形结构，例如0x43节的线段树，有很大的相似之处。我们把区间DP作为线性DP中一类重要的分支单独进行讲解，使下一节树形DP的内容更容易理解。同时，借助区间DP这种与树形相关的结构，我们也将提及记忆化搜索——其本质是动态规划的递归实现方法。

“多边形”是一款单人益智游戏。在游戏开始时，系统给定玩家一个$N$边形，该$N$边形由$N$个顶点和$N$条边构成，每条边连接两个相邻的顶点。在每个顶点上写有一个整数，可正可负。在每条边上标有一个运算符“+”（加号）或“*”（乘号）。

第一步，玩家选择一条边，将它删除。接下来在进行$N-1$步，在每一步中，玩家选择一条边，把这条边以及该边连接的两个顶点用一个新的顶点代替，新顶点上的整数值等于删去的两个顶点上的数按照删去的边上标有的符号进行计算得到的结果。如下图所示，就是一盘游戏的过程。

最终，游戏仅剩一个顶点，顶点上的数值就是玩家的得分，上图玩家得分为 0。

请计算对于给定的$N$边形，玩家最高能获得多少分，以及第一步有哪些策略可以使玩家获得最高得分。

$3\le N\le 50$,
数据保证无论玩家如何操作，顶点上的数值均在$[-32768,32767]$之内。

在枚举第一步删除哪条边后，这道题就与“石子合并”非常相似，仍是在每一步中对两个相邻的元素做某种运算合成一个。简便起见，我们把被删除的边逆时针方向的顶点称为“第一个顶点”，依次类推。容易想到使用$F[l,r]$表示把$l$到$r$个顶点合成一个顶点后，顶点上的数值最大是多少。

然而，在使用动态规划解决每一道问题时，都时刻牢记动态规划的“三要素”和使用动态规划的“三前提”。把“顶点上的最大数值”作为每一个子问题$[l,r]$的代表信息，不符合动态规划的“最优子结构”性质。因为负数的存在，进行乘法运算时，大区间$[l,r]$的顶点的最大数值不能由区间$[l,k]$和区间$[k+1,r]$合成的两个顶点的最大数值导出——因为区间$[l,k]$和区间$[k+1,r]$合成的两个顶点的最小数值可能是很小的负数，负负相乘得正，运算结果可能更大。

不过上面的反例也启发我们，如果把一个区间$[l,r]$能够合成的顶点上的最大和最小数值同时作为子问题$[l,r]$的代表信息，是否满足最优子结构性质？答案是肯定的。最大值的来源只可能是两个最大值相加、相乘，或是两个最小值相乘（负负得正），或一个最大值与一个最小值相乘（当其中一个子区间的最大、最小值都是正数，而另一个都是负数时）。最小值的来源只可能是两个最小值相加、相乘，或是两个最大值相乘，或一个最大值与一个最小值相乘。

因此，可以设$f[l,r,1]$表示把第$l$到$r$个顶点合成一个顶点后，顶点上的数值最大是多少，设$f[l,r,0]$表示把第$l$到$r$个顶点合成一个顶点后，顶点上的数值最小是多少。枚举区间的划分点$k$（决策），状态转移方程如下：
f [ l ] [ r ] [ 1 ] = max ⁡ l ≤ k < r { f [ l ] [ k ] [ 1 ] + f [ k + 1 ] [ r ] [ 1 ] f [ l ] [ k ] [ p ] ∗ f [ k + 1 ] [ r ] [ q ] , p , q ∈ { 0 , 1 } f[l][r][1]=\underset{l\leq k <r}\max \left\{\begin{array}{l}f[l][k][1]+f[k+1][r][1] \\ f[l][k][p]*f[k+1][r][q],p,q\in\{0,1\} \end{array}\right. f[l][r][1]=l≤k<rmax​{f[l][k][1]+f[k+1][r][1]f[l][k][p]∗f[k+1][r][q],p,q∈{0,1}​

f [ l ] [ r ] [ 0 ] = min ⁡ l ≤ k < r { f [ l ] [ k ] [ 0 ] + f [ k + 1 ] [ r ] [ 0 ] f [ l ] [ k ] [ p ] ∗ f [ k + 1 ] [ r ] [ q ] , p , q ∈ { 0 , 1 } f[l][r][0]=\underset{l\leq k <r}\min \left\{\begin{array}{l}f[l][k][0]+f[k+1][r][0] \\ f[l][k][p]*f[k+1][r][q],p,q\in\{0,1\} \end{array}\right. f[l][r][0]=l≤k<rmin​{f[l][k][0]+f[k+1][r][0]f[l][k][p]∗f[k+1][r][q],p,q∈{0,1}​

初值：$\forall l\in [1,N],F[l,l,0]=F[l,l,1]=A_l$，其余均为正或负无穷。

目标：$F[1,N,1]$。

上述算法的时间复杂度为$O(N^4)$。实际上我们还可以进一步优化掉枚举第一步删除哪条边耗费的时间。在游戏最初，我们选择一条边删掉，然后把剩下的“链”复制一倍接在末尾（以被删除的边逆时针方向的第一个顶点为开头），如下图所示：

在这个边长为$2N$的“链”上，$\forall i\in [1,N]$的区间$[i,i+N-1]$合并成一个顶点，就等价于原游戏的第一步删掉第$i$个顶点逆时针一侧的边，然后把剩余的部分合并成一个顶点。因为区间长度是DP的阶段，我们只需要对前$N$个阶段进行DP，每个阶段只有不超过$2N$个状态总时间复杂度降低为$O(N^3)$。最后的答案是 max ⁡ 1 ≤ i ≤ N { F [ i , i + N − 1 ] } \underset{1\leq i\leq N} \max\{ F[i,i+N-1] \} 1≤i≤Nmax​{F[i,i+N−1]}。

#include <bits/stdc++.h>
using namespace std;

int N;
int a[110];
char op[110];
int dp[110][110][2];

int main()
{
	scanf("%d",&N);
	for(int i=1;i<=N;++i)
	{
		getchar();
		scanf("%c %d",&op[i],&a[i]);
	}
	for(int i=N+1;i<=2*N;++i)
		op[i]=op[i-N],a[i]=a[i-N];
	for(int i=1;i<=2*N;++i)
		for(int j=1;j<=2*N;++j)
			dp[i][j][0]=0x3f3f3f3f,dp[i][j][1]=0xcfcfcfcf;
	for(int len=1;len<=N;++len)
	{
		for(int l=1;l+len-1<=2*N;++l)
		{
			int r=l+len-1;
			if(len==1)
			{
				dp[l][r][0]=dp[l][r][1]=a[l];
				continue;
			}
			for(int k=l;k<r;++k)
			{
				if(op[k+1]=='t')
				{
					dp[l][r][0]=min(dp[l][r][0],dp[l][k][0]+dp[k+1][r][0]);
					dp[l][r][1]=max(dp[l][r][1],dp[l][k][1]+dp[k+1][r][1]);
				}
				else
				{
					for(int i=0;i<2;++i)
						for(int j=0;j<2;++j)
						{
							dp[l][r][0]=min(dp[l][r][0],dp[l][k][i]*dp[k+1][r][j]);
							dp[l][r][1]=max(dp[l][r][1],dp[l][k][i]*dp[k+1][r][j]);
						}
				}
			}
		}
	}
	int ans=0xcfcfcfcf;
	for(int i=1;i<=N;++i)
		ans=max(ans,dp[i][i+N-1][1]);
	printf("%d\n",ans);
	for(int i=1;i<=N;++i)
		if(ans==dp[i][i+N-1][1])
			printf("%d ",i);
	return 0;
}

这种“任意选择一个位置断开，复制形成两倍长度的链”的方法，是解决DP中环形结构的常用手段之一，我们会在0x55节进一步探讨。

虽然探索金字塔是极其老套的剧情，但是有一队探险家还是到了某金字塔脚下。

经过多年的研究，科学家对这座金字塔的内部结构已经有所了解。

首先，金字塔由若干房间组成，房间之间连有通道。

如果把房间看作节点，通道看作边的话，整个金字塔呈现一个有根树结构，节点的子树之间有序，金字塔有唯一的一个入口通向树根。

并且，每个房间的墙壁都涂有若干种颜色的一种。

探险队员打算进一步了解金字塔的结构，为此，他们使用了一种特殊设计的机器人。

这种机器人会从入口进入金字塔，之后对金字塔进行深度优先遍历。

机器人每进入一个房间（无论是第一次进入还是返回），都会记录这个房间的颜色。

最后，机器人会从入口退出金字塔。

显然，机器人会访问每个房间至少一次，并且穿越每条通道恰好两次（两个方向各一次）， 然后，机器人会得到一个颜色序列。

但是，探险队员发现这个颜色序列并不能唯一确定金字塔的结构。

现在他们想请你帮助他们计算，对于一个给定的颜色序列，有多少种可能的结构会得到这个序列。

因为结果可能会非常大，你只需要输出答案对$10^9$取模之后的值。

输入仅一行，包含一个字符串 $S$，长度不超过 300，表示机器人得到的颜色序列。

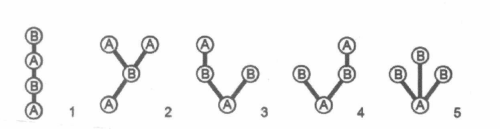
例如序列“ABABABA”对应5种金字塔结构，最底层是树根。我们认为子树之间是有序的，所以方案3和方案4是两种不同的方案。如下图所示。

在0x21节中我们提到过，一棵树的每棵子树都对应着这棵树的DFS序中的一个区间。本题中记录的序列虽然不是DFS序，但仍满足这条性质。因此，这道题目在“树形结构”与“字符串”之间通过“子树”和“区间”建立了联系。结合本节前半部分对区间DP的分析，不难想到用$F[l,r]$表示子串$S[l\sim r]$对应着多少种可能得金字塔结构（树形结构）。

接下来我们考虑对区间的划分。以上图中的方案3为例，序列“ABABABA”被分成五个部分：

同理，方案5把序列分成“A|B|A|B|A|B|A”七个部分。也就是说，若子串$S[l\sim r]$对应一棵子树，则$S[l+1],S[r-1]$两个字符是进入和离开时产生的。除此之外，$[l,r]$包含的每棵更深的子树都对应着一个子问题，会产生$[l,r]$中的一段。相邻两段之间还有途径树根产生的一个字符。因此，$[l,r]$包含的子树个数可能不止两个，如果我们像前面的题目一样，采用朴素算法枚举子串$S[l\sim r]$划分点的数量和所有划分点的位置，那么时间复杂度会变得非常高。

把子串$S[l\sim r]$分成两部分，每部分可由若干棵子树组成。不过这样可能会产生重复计数。如果每段可以由多颗子树构成，那么划分方案“A|BAB|A|B|A”和“A|B|A|BAB|A”中的”BAB“都能产生”B|A|B“两颗子树，最终归为同一结果——方案5。

实际上，为了解决让计数不重不漏，我们可以只考虑子串$S[l\sim r]$的第一棵子树是由哪一段构成的。枚举划分点$k$，令子串$S[l+1\sim k-1]$构成$[l,r]$的第一棵子树，$S[k\sim r]$构成$[l,r]$的剩余部分（其他子树）。如下图所示。

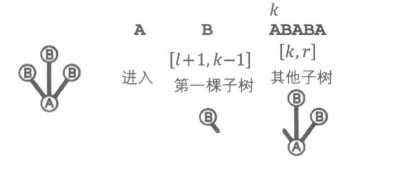
如果$k$不相同，那么子串$S[l+1\sim k-1]$代表的子树的大小也不相同，就不可能产生重复计算的结构。于是，我们可以得到状态转移方程：
$$F[l,r]=\{\begin{array}{l}0,S[l]\ne S[r]\\ \sum _{l+2\le k\le r,S[l]=S[k]}F[l+1,k-1]\ast F[k,r],S[l]=S[r]\end{array}$$
初值，$\forall l\in [1,N],F[l,l]=1$，其余均为0。目标：$F[1,N]$。

这道题告诉我们，对于方案计数类的动态规划问题，通常一个状态的各个决策之间满足“加法原理”，而每个决策划分之间的几个子状态满足“乘法原理”。在设计状态转移方程的决策方案与划分方法时，一个状态的所有决策之间必须具有互斥性，才能保证不会出现重复问题。在0x5c节中我们会进一步探讨计数类DP的相关模型与求解策略。

#include <bits/stdc++.h>
using namespace std;

char s[305];
int dp[305][305];
const int p=1e9;

int main()
{
	scanf("%s",s+1);
	int N=strlen(s+1);
	for(int len=1;len<=N;++len)
	{
		for(int l=1;l+len-1<=N;++l)
		{
			int r=l+len-1;
			if(len==1)
			{
				dp[l][r]=1;
				continue;
			}
			if(s[l]==s[r])
				for(int k=l+2;k<=r;++k)
				    if(s[l]==s[k])
					    dp[l][r]=(dp[l][r]+dp[l+1][k-1]*(long long)dp[k][r])%p;
		}
	}
	printf("%d",dp[1][N]);
	return 0;
}

在具体的程序编写中，区间DP不仅可以用递推（若干循环）来实现，也可以用递归（记忆化搜索）来实现。把子问题的求解过程写成一个函数$solve(l,r)$，枚举划分点$k$，递归求解$solve(l+1,k-1)$和$solve(k,r)$，回溯时把二者的结果相乘，加到$solve(l,r)$的结果中。在上述过程中，一个区间$[l,r]$对应的函数$solve(l,r)$可能会被调用多次，我们可以建立一个全局函数$F$，在第一次计算完$solve(l,r)$时把结果保存在$F[l,r]$中，之后$solve(l,r)$再被调用时就可以直接返回$F[l,r]$。这样带有记忆化的搜索就保证了每个区间只会求解一次，时间复杂度仍然是$O(N^3)$。

int f[305][305],p=1e9;
int solve(int l,int r)
{
    if(l>r) return 0;
    if(l==r) return 1;
    if(f[l][r]!=-1) return f[l][r]; //记忆化
    f[l][r]=0;
    for(int k=l+2;k<=r;++k)
        f[l][r]=(f[l][r]+(long long)solve(l+1,k-1)*solve(k,r))%p;
    return f[l][r];
}

memset(f,-1,sizeof(f));
solve(1,N);