【一(18)】填空题

• 计算矩阵的Jordan标准形

  • 能分块先分块（ 但反求对应的广义特征向量不可分块）；
  • 分块对角阵，可以按块分别求Jordan标准形【11、13、16、17】；
  • 2，3阶用特征向量法（P9），4阶及以上用Smith标准形法；
  • 矩阵求特征多项式，2，3阶套公式，4阶以上利用初等变换（包括行、列变换，不改变行列式的值）化简计算；
  • 计算相似变换矩阵P（P15-16）【14】。

• 计算向量/矩阵范数

  • 向量范数
    $$\begin{gathered} \Vert x{\Vert }_1=\sum _{k=1}^n|{\xi }_k| \\ \Vert x{\Vert }_2=\sqrt{\sum _{k=1}^n|{\xi }_k{|}^2}=\sqrt{x^{H}x} \\ \Vert x{\Vert }_{\infty }=\underset{k}{\max }|{\xi }_k| \\ {\Vert x{\Vert }_p=(\begin{array}{c}{\sum }_{k=1}^n|{\xi }_k{|}^p\end{array})}^{\frac{1}{p}} \\ \Vert x{\Vert }_A=\sqrt{x^{H}Ax},A为Hermite正定矩阵. \end{gathered}$$

  • 矩阵范数
    $$\begin{gathered} \Vert A{\Vert }_{m_1}=\sum _{i=1}^m\sum _{j=1}^n|a_{ij}| \\ \Vert A{\Vert }_F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n{\left|a_{ij}\right|}^2}=\sqrt{tr(A^{H}A)} \\ \Vert A{\Vert }_{m_{\infty }}=n\underset{i,j}{\max }|a_{ij}| \\ \Vert A{\Vert }_1=\underset{j}{\max }\sum _{i=1}^n|a_{ij}| \\ \Vert A{\Vert }_2=\sqrt{A^{H}A\text{的最大特征值}} \\ \Vert A{\Vert }_{\infty }=\underset{i}{\max }\sum _{j=1}^n|a_{ij}| \end{gathered}$$

    若A是正规矩阵（例如实对称矩阵），$\Vert A{\Vert }_2$为$A$的最大特征值。

    $$\begin{gathered} 1+2+3+...+n=\frac{n(n+1)}{2} \\ {1}^2+2^2+3^2+...+n^2=\frac{n(n+1)(2n+1)}{6} \end{gathered}$$

  看清到底是向量范数还是矩阵范数！！！

• 计算矩阵的M-P逆

  • $(A\otimes B{)}^{+}=A^{+}\otimes B^{+}$。考点！！！；

  • $A^{(1)}$的计算【21】。
    $$\begin{gathered} SAP=\left[\begin{array}{cc}{I}_r& K\\ O& O\end{array}\right],A\in C_r^{m\times n}(r>0),S\in C_m^{m\times m} \\ S为变换矩阵，P为n阶(列)置换矩阵。 \end{gathered}$$
    $A^{(1)}$为：
    $$X=P\left[\begin{array}{cc}{I}_r& O\\ O& L\end{array}\right]S,X\in C^{n\times m},L\in C^{(n-r)\times (m-r)}$$
    当上式中$L=O$时，$X$为$A^{(1,2)}$。

  • 

  

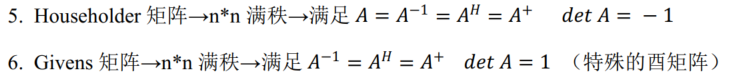
• 线性空间

• 矩阵的直积【11、14、15、16、20、21】

  • 不会单独考直积的计算和性质，一般结合范数、广义逆出题；
  • 正交投影矩阵$A$，$A^2=A,A^H=A$，$\lambda (A)=0or1$；
  • 投影矩阵$A$，$A^2=A$；
  • 酉矩阵A，$A^{H}A=I,A^H=A^{-1}$；

  

• 矩阵函数

  • 已知$f(At)$求$A$。【11、12】

    已知$e^{At}$求$A$。

    首先计算$\frac{\text{d}{e}^{At}}{\text{d}t}=A{e}^{At}$（对矩阵中每个函数分别求导），令$t=0$，即可求得$A$。（$\sin At$同思路）

  • 公式计算【15、17】

    

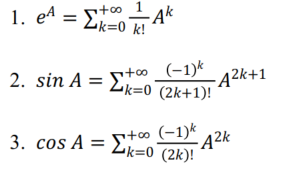
【二(10)】范数证明

• Holder不等式
  $$\sum _{k=1}^n|{\xi }_k||{\eta }_k|\le (\sum _{k=1}^n|{\xi }_k{|}^p{)}^{\frac{1}{p}}(\sum _{k=1}^n|{\eta }_k{|}^q{)}^{\frac{1}{q}}$$
  上式中，$p>1,q>1,且\frac{1}{p}+\frac{1}{q}=1.$

  当 $p=q=2$ 时，即得到 Cauchy-Schwarz 不等式。
  $$\sum _{k=1}^n|{\xi }_k||{\eta }_k|\le \sqrt{(\sum _{k=1}^n|{\xi }_k{|}^2)(\sum _{k=1}^n|{\eta }_k{|}^2)}$$

• $C=AB,c_{ij}={\sum }_{k=1}^n{a}_{ik}{b}_{kj}$

• 对称正定矩阵$A$满足：存在可逆矩阵$P$使得$A=P^{H}P$

• 几种常见的不等式

  • $\sqrt{({\sum }_{k=1}^n|{\xi }_k{|}^2)({\sum }_{k=1}^n|{\eta }_k{|}^2)}\le ({\sum }_{k=1}^n|{\xi }_k|)({\sum }_{k=1}^n|{\eta }_k|)$

  • $|{\sum }_{k=1}^n{a}_{ik}{b}_{kj}|\le {\sum }_{k=1}^n|a_{ik}{b}_{kj}|={\sum }_{k=1}^n|a_{ik}||b_{kj}|$

  • $(ab+cd{)}^2\le (a^2+c^2)(b^2+d^2)$ 【柯西不等式】

    在证明范数三角不等式或相容性时可以使用。

【三(15)】矩阵函数

1 计算 $e^{At}$

采用待定系数法求解，P71，例3.10。

• Step1：求矩阵A的特征多项式$det(\lambda I-A)$，并求出最小多项式$m_A(\lambda )$；

  特征多项式计算：

  $(\lambda +a)(\lambda +b)(\lambda +c)={\lambda }^3+(a+b+c){\lambda }^2+(ab+ac+bc)\lambda +abc$

  最小多项式计算：试探法，P21。

• Step2：根据最小多项式的最高次次数$n$，设待定方程
  $$f(\lambda )=e^{\lambda t}=m_A(\lambda )q(\lambda )+b_{n-1}{\lambda }^{n-1}+...+b_1\lambda +b_0$$
  接着，根据特征值及其重数（决定是否求导）列出方程组，求解得到系数$b_0,b_1,...,b_{n-1}$；

• Step3：将$A$代入上式计算$e^{At}$。
  $$e^{At}=b_{n-1}{A}^{n-1}+...+b_{1}A+b_{0}I$$

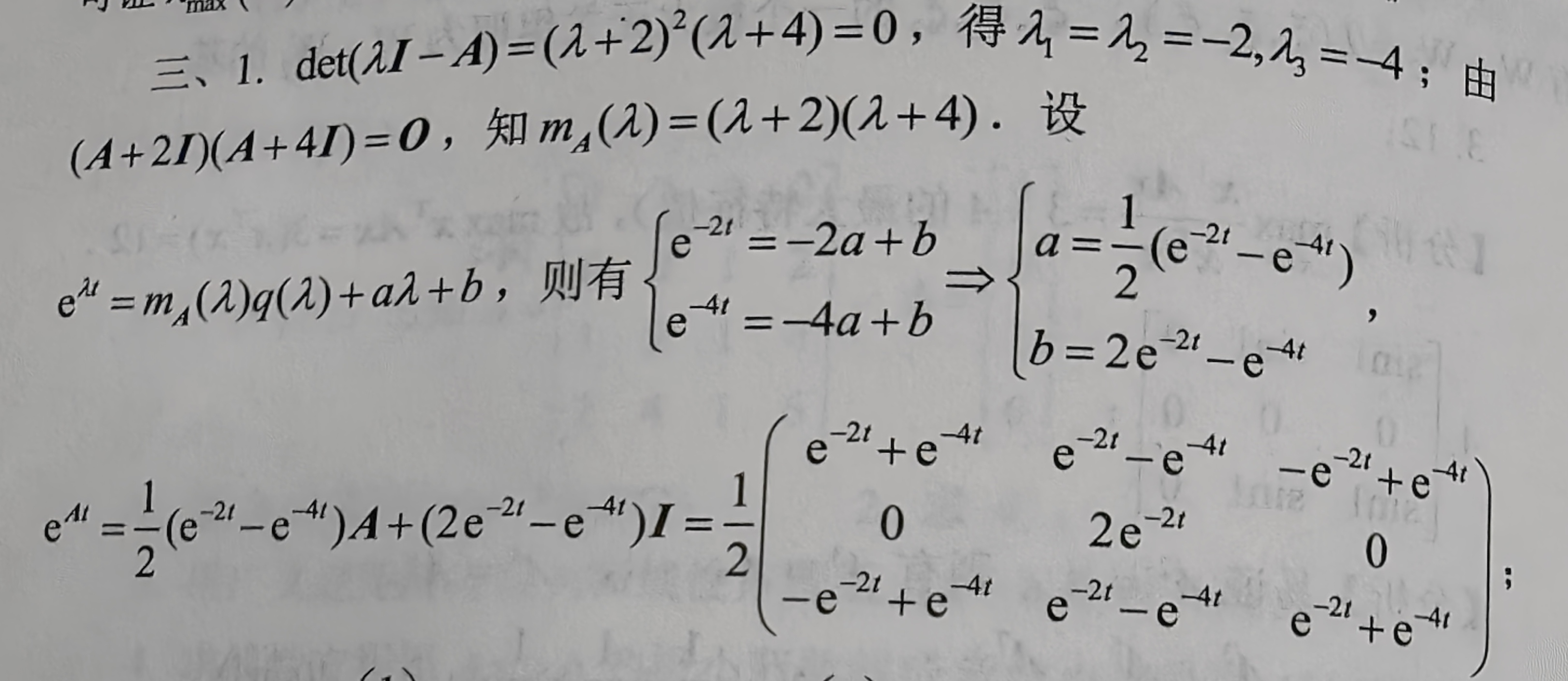
本题题型只涉及3阶矩阵，且最小多项式为最高次数为2（要么两个不同特征值，要么一个2重根的特征值，后者需要求一阶导建立一个方程，注意是对$\lambda$求导，$t$为参数），即待定系数只有2个。

2 求微分方程的解

• Step1：计算$e^{-A\tau }b(\tau )$；

  其中$e^{-A\tau }$便是将$e^{A\tau }$矩阵中每个元素中的$\tau$用$-\tau$替换后的矩阵。

• Step2：计算${\int }_0^t{e}^{-A\tau }b(\tau )d\tau$；

  ${\int }_a^{b}A(t)dt=({\int }_a^b{a}_{ij}(t)dt{)}_{m\times n}$

• Step3：计算$x(t)$。

  $x(t)=e^{At}x(0)+e^{At}{\int }_0^t{e}^{-A\tau }b(\tau )d\tau$

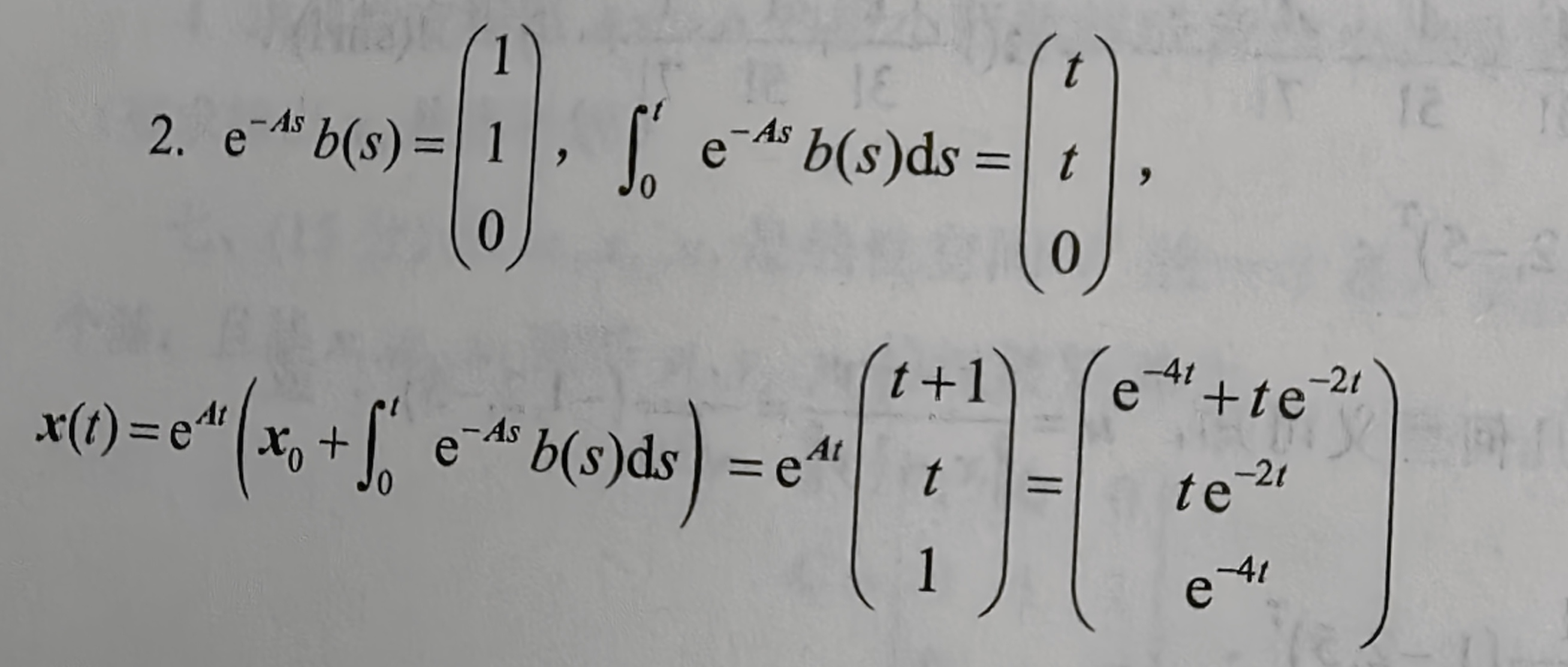
历年考卷中一般本题积分项结果都很简单。

刷题总结

• 注意$\lambda I-A$计算时，除了将$A$对角线元素用$\lambda$减去外，其他元素应被$0$减去，即取负。

• 计算 $e^{At}$时，常数项应当乘以一个单位矩阵，在计算两个矩阵元素对应相加时，注意只有对角线元素需要加上常数项值。

• 在计算过程中将$e$的幂次项提出来，方便计算。

【四(10)】QR分解

这道题固定为使用Householder变换或Givens变换求解4阶矩阵A的QR分解。

矩阵乘法计算容易出错😢

Householder变换是镜像变换，不改变向量的长度。

【五(10)】Gerschgorim隔离特征值

本题题型：

• 利用盖尔圆隔离矩阵A（4阶，偶尔3阶）的特征值，并画图表示。

• 利用实矩阵特征值的性质改进所得结果。

  实矩阵的特征值必为实数，于是A的特征值分别在区间……中。

• 证明矩阵可逆。

  矩阵可逆的充要条件$|A|\ne 0$，即证明0不是不是矩阵A的特征值（0不在盖尔圆内部）。

【六(15)】$A^{+}$计算及求解线性方程组

1 计算满秩分解

• Step1：初等行变换将$A$矩阵变为Hermite标准形（行最简形）$H$；
• Step2：取$A$的第$j_1,j_2,...j_r$（$j_i$为第$i$行的第一个非零元素$1$位于的列）列构成矩阵$F$（列满秩），取$H$的前$r$行构成矩阵$G$（行满秩）。

2 计算$A^{+}$

$$A^{+}=G^H(G{G}^H{)}^{-1}(F^{H}F{)}^{-1}{F}^H$$

这道题也可能是已知$A^{+}$求$A$，利用性质$(A^{+}{)}^{+}=A$即可计算。

3 判断线性方程组解是否存在

线性方程组有解的充要条件为：
$$A{A}^{+}b=b$$
极小范数解（有解）或极小范数最小二乘解（无解）为：
$$x=A^{+}b$$

先算$A^{+}b$的值，在算$A{A}^{+}b$。

【七(15)】线性空间与线性变换

求线性变换T在一组基下的矩阵

$$T({\alpha }_1,{\alpha }_2,...,{\alpha }_n)\triangleq (T({\alpha }_1),T({\alpha }_2),...,T({\alpha }_n))=({\alpha }_1,{\alpha }_2,...,{\alpha }_n)A$$

同一个线性变换在不同基下的矩阵关系：
$$\begin{gathered} T({\alpha }_1,{\alpha }_2,...,{\alpha }_n)=({\alpha }_1,{\alpha }_2,...,{\alpha }_n)A, \\ T({\beta }_1,{\beta }_2,...,{\beta }_n)=({\beta }_1,{\beta }_2,...,{\beta }_n)B, \\ ({\beta }_1,{\beta }_2,...,{\beta }_n)=({\alpha }_1,{\alpha }_2,...,{\alpha }_n)P, \\ \Rightarrow T({\beta }_1,{\beta }_2,...,{\beta }_n)=T[({\alpha }_1,{\alpha }_2,...,{\alpha }_n)P]=T({\alpha }_1,{\alpha }_2,...,{\alpha }_n)P \\ =({\alpha }_1,{\alpha }_2,...,{\alpha }_n)AP=({\beta }_1,{\beta }_2,...,{\beta }_n)P^{-1}AP \end{gathered}$$

生成子空间的基与维数

某组基（自然基）下坐标向量组的极大无关组与秩 $\iff$ 元素组的极大无关组和秩 $\iff$ 生成子空间的基与维数。

线性变换矩阵的化简（相似对角化）

证明线性变换是对称变换

即证明线性变换在线性空间的一组基下的矩阵为对称矩阵。

不变子空间证明