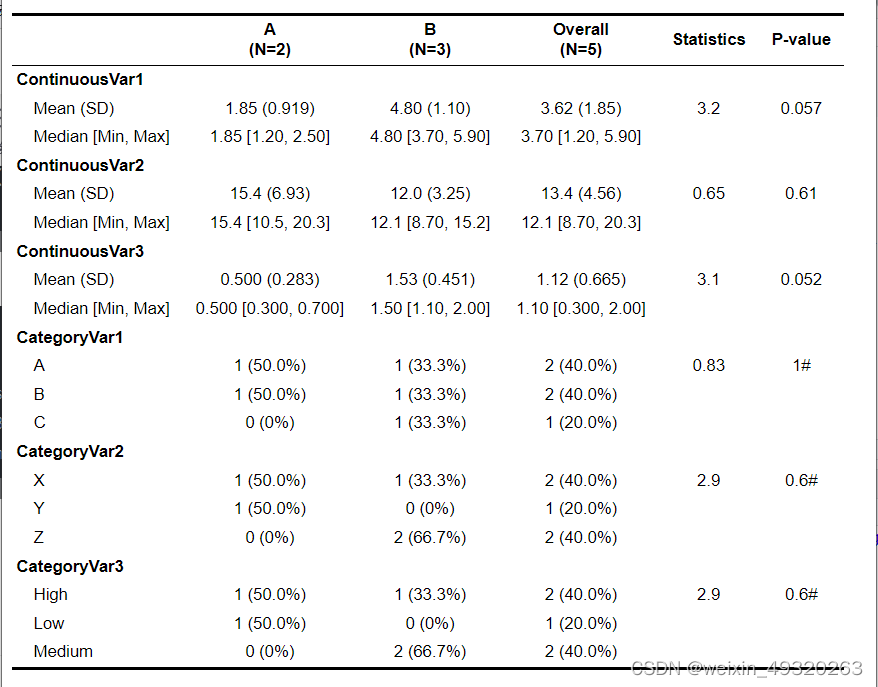
R语言的优势在于批量处理，常使用到循环和函数，三线表是科研文章中必备的内容。利用函数实现自动判断数据类型和计算。使用R包（table1）。

# 创建连续性变量
continuous_var1 <- c(1.2, 2.5, 3.7, 4.8, 5.9)
continuous_var2 <- c(10.5, 20.3, 15.2, 8.7, 12.1)
continuous_var3 <- c(0.3, 0.7, 1.1, 2.0, 1.5)

# 创建分类变量
category_var1 <- factor(c("A", "B", "A", "C", "B"))
category_var2 <- factor(c("X", "Y", "Z", "X", "Z"))
category_var3 <- factor(c("High", "Low", "Medium", "Medium", "High"))

# 创建data.frame
df <- data.frame(
  ContinuousVar1 = continuous_var1,
  ContinuousVar2 = continuous_var2,
  ContinuousVar3 = continuous_var3,
  CategoryVar1 = category_var1,
  CategoryVar2 = category_var2,
  CategoryVar3 = category_var3
)

# 显示data.frame
df

#generate three line table
#pvalue
pvalue <- function(x, name, ...){
  y <- df[[name]]#variable
  g <- df[,"Group"]#Group
  if (is.numeric(y)) {
    if (shapiro.test(y)$p.value>0.05){
      p <- t.test(y ~ g)$p.value
      p_with_symbol <- paste0(format.pval(p, digits = 3, eps = 0.001), "*")
    }else{
      p <- wilcox.test(y ~ g)$p.value
      p_with_symbol <- paste0(format.pval(p, digits = 3, eps = 0.001), "**")
      }
  }else{
    if (length(y) > 40 & any(sapply(chisq.test(y,g)$expected, function(x) x >=1))){
      p <- chisq.test(y, g)$p.value
      p_with_symbol <- paste0(format.pval(p, digits = 3, eps = 0.001,trim = FALSE), "#")
      } else {
        p<-fisher.test(y,g)$p.value
        p_with_symbol <- paste0(format.pval(p, digits = 3, eps = 0.001), "##")
      }
  }
  c("",  p_with_symbol)
}

#自定义函数准备显示统计值(t值或卡方值)
stat_value <- function(x, name, ...) {
  y <- df[[name]] # 变量
  g <- df[,"Group"] # 分组变量
  if (is.numeric(y)) {
    # 连续变量使用 t 检验或 Mann-Whitney U 测试
    if (shapiro.test(y)$p.value > 0.05) {
      s <- abs(t.test(y ~ g)$statistic[["t"]]) # 正态分布，使用 t 检验
    } else {
      s <- wilcox.test(y ~ g)[["statistic"]][["W"]] # 非正态分布，使用 Mann-Whitney U 测试
    }
  } else {
    if(length(y) > 40 & any(sapply(chisq.test(y,g)$expected, function(x) x >=1))){
      s<-chisq.test(y, g)$statistic[["X-squared"]]
    } else {
      s<-fisher.test(y, g)$statistic[["X-squared"]]
    }
    # 分类变量使用卡方检验
    s <- chisq.test(y, g)$statistic[["X-squared"]]
  }
  c("",  format.pval(s, digits=3, eps=0.001))
}
#定义变量的展现形式
# rndr <- function(x, name, ...) {
#   if (!is.numeric(x)) return(render.categorical.default(x))
#   what <- switch(name,
#                  Age = "Median [Min, Max]",
#                  `Survival months` = "Median [Min, Max]"
#   )
#   parse.abbrev.render.code(c("", what))(x)
# }

#绘图
library(table1)
paste(sprintf("`%s`",colnames(df)),collapse="+")
df$Group<-c(rep("A",2),rep("B",3))
table<-table1(~`ContinuousVar1`+`ContinuousVar2`+`ContinuousVar3`+`CategoryVar1`+`CategoryVar2`+`CategoryVar3`|Group,ender=rndr,data=df,extra.col=list(`Statistics`=stat_value,`P-value`=pvalue))

#保存为docx
library(flextable);help(package="flextable")
table_fl<-t1flex(table)
save_as_docx(table_fl,path="table.docx")