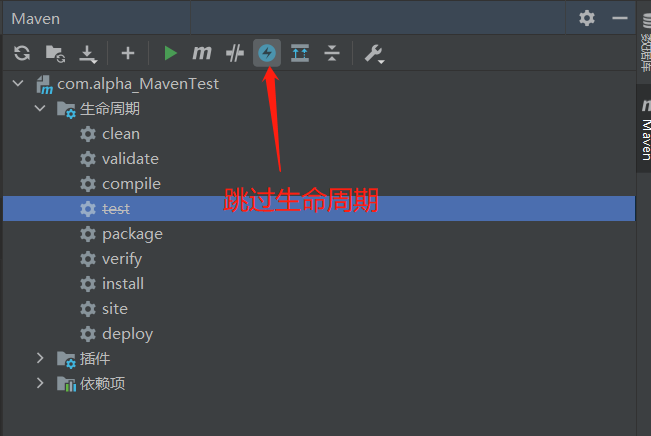
本文仅供学习使用
本文参考：
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任

---

连杆机构中的连杆与连架杆构成运动副，该运动副元素的特征点或特征线在机架坐标系中的运动轨迹曲线或曲面称为约束曲线或约束曲面，是联系刚体运动与机构运动综合的桥梁，其几何性质是机构运动综合的理论基础，既是曲线与曲面的几何学研究内容，也是连杆机构运动几何学分析与综合的课题。然而，研究曲线与曲面的几何学，微分几何学方法无疑是自然而然的选择，将其与机构运动学结合，形成以点与线的运动方式研究约束曲线与曲面几何性质，为机构运动几何学分析与综合提供理论依据。
为方便阅读后续内容，在第3.1和第3.2节简单概述微分几何学基本知识；采用微分几何量方法研究连杆机构中典型而又重要的约束曲线与约束曲面，称为空间约束曲线与约束曲面微分几何学。

3.1 空间曲线微分几何学概述

3.1.1 矢量表示

在直角坐标中表达一条空间曲线$\Gamma$时，有：
$$\{\begin{array}{c}x=x(t)\\ y=y(t)\\ z=z(t)\end{array}$$
式中，$t$为曲线的参数，若置换自变量或者消去参数$t$,则可写成：
$$\{\begin{array}{c}y=y(x)\\ z=z(x)\end{array}$$
或者写成隐函数形式：
$$\{\begin{array}{c}{F}_1(x,y,z)=0\\ F_2(x,y,z)=0\end{array}$$
若将上述$x,y,z$置于空间固定坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中，则曲线$\Gamma$以参数$t$表示的矢量方程为：
$$\Gamma :R=x(t)i+y(t)j+z(t)k$$
可以将其简化为:
$$R=R(t)$$
式(3.4)和式(3.5)为空间曲线$\Gamma$的矢量表达式，$t$为曲线$\Gamma$的一般参数。在 第1章平面曲线的微分几何学 中引入了圆矢量函数用来描述曲线的矢量方程，使得形式简洁并便于计算。因此对于空间曲线$\Gamma$的矢量方程式(3.4),可以选择任意两个坐标轴上的分量用圆矢量函数进行描述。例如，将曲线$\Gamma$上任意点的矢径在坐标平面$O-ij$上的投影矢量用圆矢量函数描述，如下图所示。

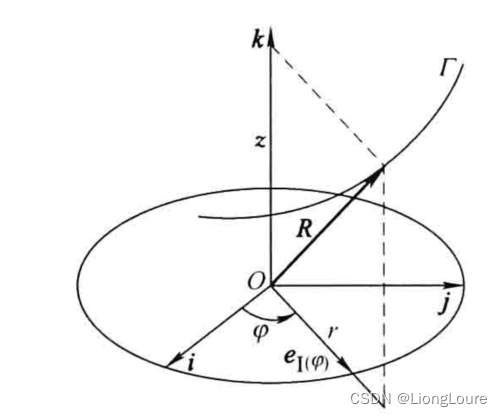
则其矢量方程可以写出另一种形式：
$$\Gamma :R=r(\phi )e_{I(\phi )}+z(\phi )k$$
对于空间曲线$\Gamma$，弧长参数$s$为其自然参数，且与一般参数$t$的关系为：
$$s={\int }_{t_a}^{t_b}\left|\frac{dR}{dt}\right|dt,ds=\left|dR\right|=\sqrt{{(\frac{dx}{dt})}^2+{(\frac{dy}{dt})}^2+{(\frac{dz}{dt})}^2}dt$$

空间曲线$\Gamma$的矢量方程用弧长参数$s$表示为：$\Gamma :R=R(s),s_a\le s\le s_b$

注：书中为$\Gamma :R=R(s),s_a\le a\le s_b$

【例3-1】 球面曲线如下图所示：

对于球面曲线$\Gamma$,习惯于将直角坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}原点置于球心，则用直角坐标表示为：
$$\{\begin{array}{c}x=x(t),y=y(t),z=z(t)\\ x^2+y^2+z^2=R^2\end{array}$$
式中，$R$为球面半径，$t$为球面曲线的参数，若置换自变量或者消去参数$t$,可写成：
$$\{\begin{array}{c}z=z(x,y)\\ x^2+y^2+z^2=R^2\end{array}$$
由于球面曲线上的点始终分布在一球面上，因此往往用球面坐标表示曲线为：
$$\delta =\delta (t),\phi =\phi (t),r=R$$
式中，$\delta$是由原点0到曲线上点$P$的有向线段$OP$与$k$的夹角；$\phi$是$OP$在$O-ij$面上的投影与i的夹角，$\delta$和$\phi$的取值范围分别为$[0,\pi ]$和$[0,2\pi ]$。点$P$在坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中的球面坐标与直角坐标之间具有如下转换关系：
$$x=R\sin \delta \cos \phi ,y=R\sin \delta \sin \phi ,z=R\cos \delta$$
将上述$x,y,z$置于坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中，则球面曲线以参数$t$表示的矢量方程为：
$$\Gamma :R=R(t)=x(t)i+y(t)j+z(t)k$$
若通过圆矢量函数表示球面曲线的矢量方程，则为：
$$R=R\sin \delta (\phi )e_{I(\phi )}+R\cos \delta (\phi )k$$
比较式(E3-1.1)、式(E3-1.4)与式(E3-1.6)可知，采用矢量表示的球面曲线比其他方式表达要简单的多。

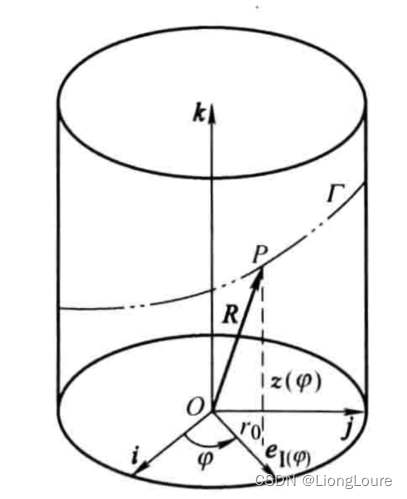
【例3-2】 圆柱面曲线如下图所示：

圆柱面曲线在直角坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中的方程为：
$$\{\begin{array}{c}x=r_0\cos \phi \\ y=r_0\sin \phi \\ z=z(\phi )\end{array}$$
式中，$r_0$为圆柱面半径。若通过圆矢量函数表示圆柱面曲线的矢量方程，则为：
$$R=r_0{e}_{I(\phi )}+z(\phi )k$$

3.1.2 Frenet标架

空间曲线 $\vec{\Gamma }:\vec{R}=\vec{R}\left(s\right)$ 在任意点$P$处有两个无限接近位置的点连线组成切线，其单位切矢$\vec{\alpha }\left(s\right)=\frac{\mathrm{d}\vec{R}\left(s\right)}{\mathrm{d}s}$始终指向曲线弧长增加的方向，将切矢$\vec{\alpha }\left(s\right)$ 对弧长参数求导，可得：

$$\frac{\mathrm{d}\vec{\alpha }\left(s\right)}{\mathrm{d}s}=k\left(s\right)\vec{\beta }\left(s\right)$$

其中，$k\left(s\right)$ 称为曲线 $\vec{\Gamma }$ 在点 $P$ 处的曲率，即三个无限接近位置点构成空间曲线在该点处的密切平面，曲率是空间曲线在密切平面内的弯曲程度，体现了曲线的切矢的倾斜角对弧长参数的变化率。与平面曲线曲率不同，空间曲线的曲率非负。$\vec{\beta }\left(s\right)$ 称为曲线 $\vec{\Gamma }$ 在点 $P$ 处的主法矢，指向了曲线在该点的曲率中心。当 $k\left(s\right)\ne 0$ 时，其倒数 $\rho \left(s\right)=1/k\left(s\right)$ 称为曲线 $\vec{\Gamma }$ 的曲率半径，则曲线 $\vec{\Gamma }$ 曲率中心$C$的矢量为：

$${\vec{R}}_{\mathrm{C}}={\vec{R}}_{\mathrm{P}}+\rho \cdot \vec{\beta }$$

由空间曲线 $\vec{\Gamma }$ 在点 $P$ 处的切矢 $\vec{\alpha }\left(s\right)$ 和主法矢 $\vec{\beta }\left(s\right)$ 可以构建矢量 $\vec{\gamma }\left(s\right)=\vec{\alpha }\left(s\right)\times \vec{\beta }\left(s\right)$ ，称之为曲线的副法矢，从而在空间曲线 $\vec{\Gamma }$ 上构造了单位右手系正交标架 $\left\{\vec{R}\left(s\right);\vec{\alpha }\left(s\right),\vec{\beta }\left(s\right),\vec{\gamma }\left(s\right)\right\}$ ，称为曲线 $\vec{\Gamma }$ 在点 $P$ 的Frenet标架。

对于空间曲线 $\vec{\Gamma }$ 在 $P$ 点的Frenet标架 $\left\{\vec{R}\left(s\right);\vec{\alpha }\left(s\right),\vec{\beta }\left(s\right),\vec{\gamma }\left(s\right)\right\}$ ，其中标矢 $\vec{\alpha }\left(s\right)$ 和 $\vec{\beta }\left(s\right)$ 确定了密切平面， $\vec{\beta }\left(s\right)$ 和 $\vec{\gamma }\left(s\right)$ 确定的平面称为法平面，而 $\vec{\alpha }\left(s\right)$ 和 $\vec{\gamma }\left(s\right)$ 确定的平面称为从切平面。可见Frenet标架由三个同空间曲线紧密联系的向量所组成，其微分运算公式为：

$$\{\begin{array}{l}\begin{array}{c}\frac{\mathrm{d}\vec{R}\left(s\right)}{\mathrm{d}s}=\vec{\alpha }\left(s\right)\\ \frac{\mathrm{d}\vec{\alpha }\left(s\right)}{\mathrm{d}s}=k\left(s\right)\vec{\beta }\left(s\right)\end{array}\\ \begin{array}{c}\frac{\mathrm{d}\vec{\beta }\left(s\right)}{\mathrm{d}s}=-k\left(s\right)\vec{\alpha }\left(s\right)+\tau \left(s\right)\vec{\gamma }\left(s\right)\\ \frac{\mathrm{d}\vec{\gamma }\left(s\right)}{\mathrm{d}s}=-\tau \left(s\right)\vec{\beta }\left(s\right)\end{array}\end{array}$$

其中，$\tau \left(s\right)$ 称为空间曲线 $\vec{\Gamma }$ 在点 $P$ 处的挠率，它衡量了曲线在点 $P$ 的(密切平面)副法矢 $\vec{\gamma}\left( s \right)$ 倾斜角对弧长的变化率，从而描述了曲线在该点偏离密切平面的程度。上式也称为空间曲线的Frenet公式。

由Frenet公式可以得到空间曲线 $\vec{\Gamma }$ 曲率 $k$ 和挠率 $\tau$ 的表达式为：

$$k=\left|\frac{{\mathrm{d}}^2\vec{R}\left(s\right)}{\mathrm{d}{s}^2}\right|,\tau =\left(\frac{\mathrm{d}\vec{R}\left(s\right)}{\mathrm{d}s},\frac{{\mathrm{d}}^2\vec{R}\left(s\right)}{\mathrm{d}{s}^2},\frac{{\mathrm{d}}^3\vec{R}\left(s\right)}{\mathrm{d}{s}^3}\right)/{\left|\frac{{\mathrm{d}}^2\vec{R}\left(s\right)}{\mathrm{d}{s}^2}\right|}^2$$

若空间曲线 $\vec{\Gamma }$ 是以一般参数 $t$ 进行描述的，则其曲率 $k(s)$ 和挠率 $\tau \left(s\right)$ 的表达式为：
$$k=\left|\frac{\mathrm{d}\vec{R}}{\mathrm{d}t}\times \frac{{\mathrm{d}}^2\vec{R}}{\mathrm{d}{t}^2}\right|/{\left|\frac{\mathrm{d}\vec{R}}{\mathrm{d}t}\right|}^3,\tau =\left(\frac{\mathrm{d}\vec{R}}{\mathrm{d}t},\frac{{\mathrm{d}}^2\vec{R}}{\mathrm{d}{t}^2},\frac{{\mathrm{d}}^3\vec{R}}{\mathrm{d}{t}^3}\right)/{\left(\frac{\mathrm{d}\vec{R}}{\mathrm{d}t}\times \frac{{\mathrm{d}}^2\vec{R}}{\mathrm{d}{t}^2}\right)}^2$$
对于空间曲线来说，曲率 $k(s)$ 和挠率 $\tau \left(s\right)$ 不依赖于坐标系的选定。是空间曲线的不变量，能够唯一地确定空间曲线，可以将 $k=k\left(s\right),\tau =\tau \left(s\right)$ 称为空间曲线的自然方程。于是有：

定理3.1：在区间 $0⩽s⩽l$上任意给定连续可微函数 $k\left( s \right) >0 $ 和连续函数 $\tau \left(s\right)$ 以及初始右手系正交标架 $\left\{{\vec{R}}_0;{\vec{\alpha }}_0,{\vec{\beta }}_0,{\vec{\gamma }}_0\right\}$ ,则一定有且仅有一条以 $s$ 为弧长、以 $k\left(s\right)$ 为曲率、 $\tau \left(s\right)$ 为挠率的空间有向曲线。

建立了空间曲线 $\vec{\Gamma }$ 上 $P$ 点处的Frenet标架 $\left\{\vec{R}\left(s\right);\vec{\alpha }\left(s\right),\vec{\beta }\left(s\right),\vec{\gamma }\left(s\right)\right\}$ ,可将曲线 $\vec{\Gamma }$ 在点$P$的邻域内按照泰勒公式展开。假定曲线 $\vec{\Gamma }$ 在点 $P$ 处的弧长为 $s$,则有：

$$\vec{R}\left(s+\Delta s\right)=\vec{R}\left(s\right)+\frac{\mathrm{d}\vec{R}\left(s\right)}{\mathrm{d}s}\Delta s+\frac{1}{2!}\frac{{\mathrm{d}}^2\vec{R}\left(s\right)}{\mathrm{d}{s}^2}{\left(\Delta s\right)}^2+\cdots +\frac{1}{n!}\frac{{\mathrm{d}}^n\vec{R}\left(s\right)}{\mathrm{d}{s}^n}{\left(\Delta s\right)}^n+{\epsilon }_{\mathrm{n}}\left(s,\Delta s\right){\left(\Delta s\right)}^n$$

式中， ${\lim }_{\Delta s\to 0}{\epsilon }_{\mathrm{n}}\left(s,\Delta s\right)=0,\frac{\mathrm{d}\vec{R}}{\mathrm{d}s}=\vec{\alpha },\frac{{\mathrm{d}}^2\vec{R}}{\mathrm{d}{s}^2}=k\vec{\beta },\frac{{\mathrm{d}}^3\vec{R}}{\mathrm{d}{s}^3}=-k^2\vec{\alpha }+\frac{\mathrm{d}k}{\mathrm{d}s}\vec{\beta }+k\tau \vec{\gamma }$ ，并以此可以得到矢径 $\vec{R}\left(s\right)$ 关于弧长参数的各阶导数。