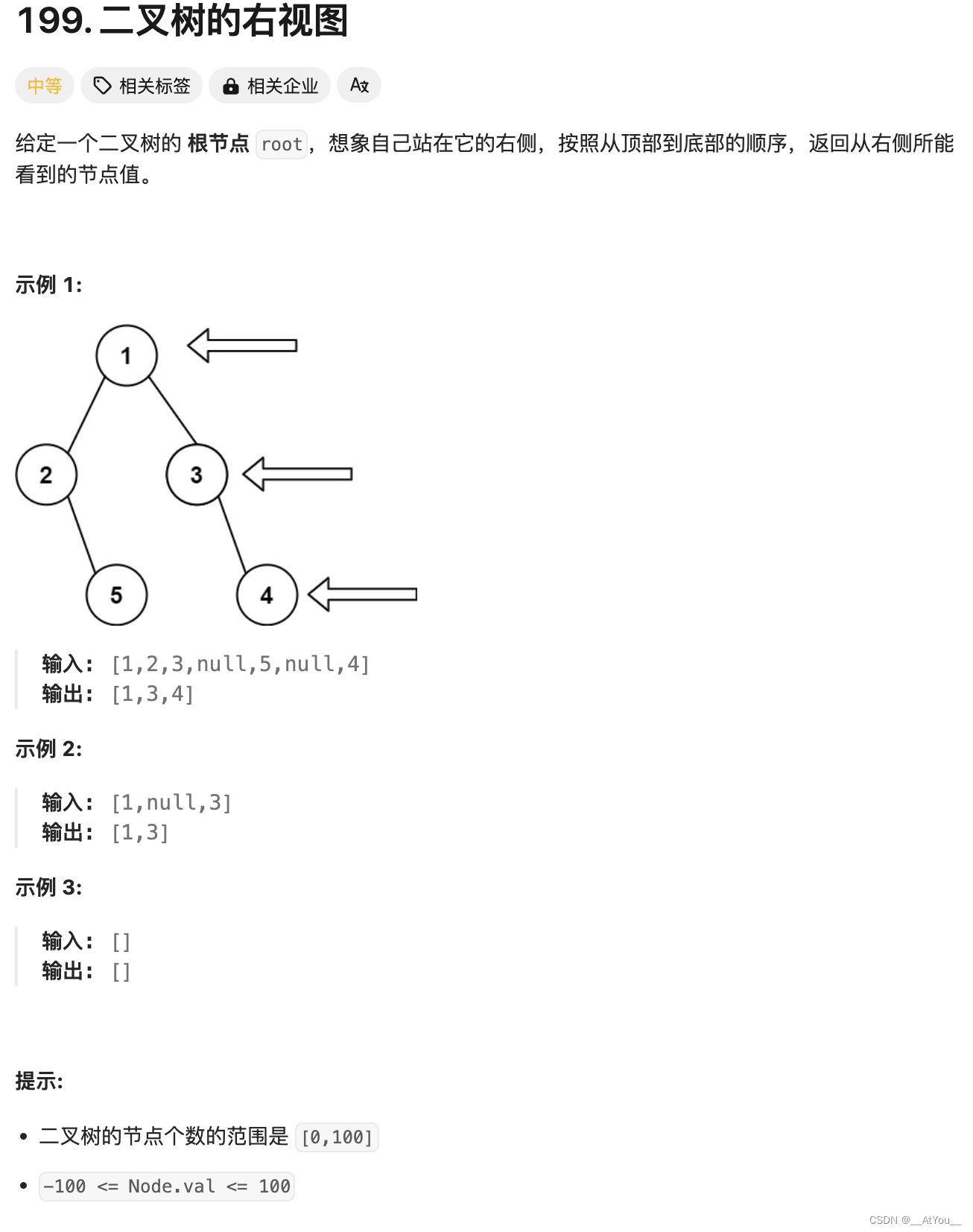
文章目录
- 1 . 瑞利商的思考
- 1.1 瑞利商的定义
- 1.2 投影向量
- 2. 拉格朗日乘子法
- 3. 鞍点
1 . 瑞利商的思考
1.1 瑞利商的定义
假设A是n阶实对称矩阵,x是n维非零列向量,那么瑞利商表示如下:
R
(
A
,
x
)
=
x
T
A
x
x
T
x
\begin{equation} R(A,x)=\frac{x^TAx}{x^Tx} \end{equation}
R(A,x)=xTxxTAx
- 在看到上面式子时候,感觉很奇怪,为什么瑞利商就能够计算出鞍点和极值点的位置?我发现瑞利商的形式就像投影公式样。。。
1.2 投影向量
假设我们有两个向量 x , a 1 x,a_1 x,a1,我们想求向量 a 1 a_1 a1在向量x方向上的投影向量 p 1 p_1 p1

- 求
∣
p
1
∣
|p_1|
∣p1∣
∣ p 1 ∣ = ∣ a 1 ∣ cos ( θ ) , x T a 1 = ∣ a 1 ∣ cos ( θ ) ⋅ ∣ x ∣ → ∣ p 1 ∣ = x T a 1 ∣ x ∣ \begin{equation} |p_1|=|a_1|\cos(\theta),x^Ta_1=|a_1|\cos(\theta)\cdot|x|\rightarrow |p_1|=\frac{x^Ta_1}{|x|} \end{equation} ∣p1∣=∣a1∣cos(θ),xTa1=∣a1∣cos(θ)⋅∣x∣→∣p1∣=∣x∣xTa1 -
p
1
p_1
p1的单位向量为:
e 1 = x ∣ x ∣ \begin{equation} e_1=\frac{x}{|x|} \end{equation} e1=∣x∣x -
p
p
p向量为:
p 1 = ∣ p 1 ∣ ⋅ e 1 = x T a ∣ x ∣ x ∣ x ∣ = x T a 1 x x T x \begin{equation} p_1=|p_1|\cdot e_1=\frac{x^Ta}{|x|}\frac{x}{|x|}=\frac{x^Ta_1x}{x^Tx} \end{equation} p1=∣p1∣⋅e1=∣x∣xTa∣x∣x=xTxxTa1x - 小结:
当我们对一个向量 a 1 a_1 a1进行瑞利商时,得到了居然是这个向量 a 1 a_1 a1在给定 x 1 x_1 x1向量上的投影向量,我们发现投影向量中只需要知道 x x x向量的方向,跟 x x x的大小无关,这点很重要, - 转换:
-那么我们有一个矩阵实对称A,它可以由如下组成:
A = [ a 1 a 2 ⋯ a n ] \begin{equation} A=\begin{bmatrix}a_1&a_2&\cdots&a_n\end{bmatrix} \end{equation} A=[a1a2⋯an] - 那么瑞利商可以表示为:
R ( A , x ) = x T [ a 1 a 2 ⋯ a n ] x x T x = [ x T a 1 x x T x x T a 2 x x T x ⋯ x T a n x x T x ] \begin{equation} R(A,x)=\frac{x^T\begin{bmatrix}a_1&a_2&\cdots&a_n\end{bmatrix}x}{x^Tx}=\begin{bmatrix}\frac{x^Ta_1x}{x^Tx}&\frac{x^Ta_2x}{x^Tx}&\cdots&\frac{x^Ta_nx}{x^Tx}\end{bmatrix} \end{equation} R(A,x)=xTxxT[a1a2⋯an]x=[xTxxTa1xxTxxTa2x⋯xTxxTanx] - 小结 : 瑞利商表示的是实对称矩阵A在给定x向量的投影向量组合。这里x的大小不影响投影向量的值。所以为了后续计算,我们可以定义
x
T
x
=
1
x^Tx=1
xTx=1,这样瑞利商问题可以变成如下:
R ( A , x ) = x T A x x T x → R ( A , x ) = x T A x , s t : x T x = 1 \begin{equation} R(A,x)=\frac{x^TAx}{x^Tx}\rightarrow R(A,x)=x^TAx,st:x^Tx=1 \end{equation} R(A,x)=xTxxTAx→R(A,x)=xTAx,st:xTx=1 - 那么瑞利商的极值问题就变成了一个二次型 x T A x x^TAx xTAx在约束条件下的 x T x = 1 x^Tx=1 xTx=1的最优化问题。一般我们解决最优化问题,会引入拉格朗日乘子法:
2. 拉格朗日乘子法
我们的目标是要求实对称矩阵S的二次型
x
T
S
x
x^TSx
xTSx在
x
T
x
=
1
x^Tx=1
xTx=1的约束情况下的最优化问题:这里为了方便,一般用S来表示实对称矩阵来代替上面的A,不影响后续理解和计算。纯粹为了方便。
L
(
S
,
λ
)
=
x
T
S
x
−
λ
(
x
T
x
−
1
)
\begin{equation} L(S,\lambda)=x^TSx-\lambda(x^Tx-1) \end{equation}
L(S,λ)=xTSx−λ(xTx−1)
- 求偏导可得:
∂ L ( S , λ ) ∂ x = 2 S x − λ ⋅ 2 x = 0 → S x = λ x \begin{equation} \frac{\partial L(S,\lambda)}{\partial x}=2Sx-\lambda \cdot 2x=0\rightarrow Sx=\lambda x \end{equation} ∂x∂L(S,λ)=2Sx−λ⋅2x=0→Sx=λx - 说明了瑞利商的偏导数为0的值一定在矩阵S的特征值
λ
\lambda
λ上和其对应的特征向量x上。
∂ L ( S , λ ) ∂ λ = − x T x + 1 = 0 → x T x = 1 \begin{equation} \frac{\partial L(S,\lambda)}{\partial \lambda}=-x^Tx+1=0\rightarrow x^Tx=1 \end{equation} ∂λ∂L(S,λ)=−xTx+1=0→xTx=1
本来都是约束条件。 - 那问题就简单了,瑞利商的极值问题的点分别为特征值 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn,其对应的特征向量 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn
- 那么我们代入到瑞利商原来式子中,可得极值特解方程,注意不是一般式:
R ( S , x ) = x T S x x T x = x T λ x x T x = λ \begin{equation} R(S,x)=\frac{x^TSx}{x^Tx}=\frac{x^T\lambda x}{x^Tx}=\lambda \end{equation} R(S,x)=xTxxTSx=xTxxTλx=λ - 由于
λ
n
≤
λ
n
−
1
≤
⋯
≤
λ
2
≤
λ
1
\lambda_n\le \lambda_{n-1}\le\cdots\le\lambda_2\le\lambda_1
λn≤λn−1≤⋯≤λ2≤λ1
arg m i n R ( S , x n ) = λ n ; arg m a x R ( S , x 1 ) = λ 1 ; \begin{equation} \arg\limits_{min}R(S,x_n)=\lambda_n;\arg\limits_{max}R(S,x_1)=\lambda_1; \end{equation} minargR(S,xn)=λn;maxargR(S,x1)=λ1; - 那么其他的特征值 λ 2 , λ 3 , ⋯ , λ n − 1 \lambda_2,\lambda_3,\cdots,\lambda_{n-1} λ2,λ3,⋯,λn−1对应的就是鞍点!!!这样我们就可以通过瑞利商来快速的找到鞍点。
3. 鞍点
在深度学习中,我们希望快速的找到极值点,一般就对损失函数求一次偏导后得到所有的极值点,但是有一种鞍点,其偏导数也为0,但是它既不是极大值点,又不是极小值点,但它的一阶偏导为0,所以我们需要排除鞍点的干扰,。如图所示:

-
鸡头法,先求最小值,再求最大值
为了求得几何上的鞍点,我们需要先求最小值,在求最大值,数学表达式如下:
λ = max y min x , z x T S x \begin{equation} \lambda=\max\limits_{y}\min\limits_{x,z}x^TSx \end{equation} λ=ymaxx,zminxTSx

-
凤尾法,先求最大值,再求最小值
λ = min x max y , z x T S x \begin{equation} \lambda=\min\limits_{x}\max\limits_{y,z}x^TSx \end{equation} λ=xminy,zmaxxTSx

-
我们可以简单理解,鸡头不如凤尾,那么我们一般是使用鸡头法,这样求得的鞍点值更小。
λ = max y min x , z x T S x \begin{equation} \lambda=\max\limits_{y}\min\limits_{x,z}x^TSx \end{equation} λ=ymaxx,zminxTSx