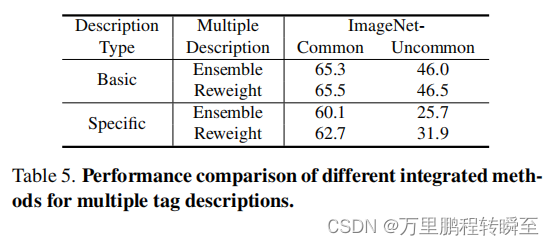
函数插值
已知函数
f
(
x
)
f(x)
f(x)在区间[a,b]上n+1个互异节点
{
x
i
}
i
=
0
n
\{{x_i}\}_{i=0}^{n}
{xi}i=0n处的函数值
{
y
i
}
i
=
0
n
\{{y_i}\}_{i=0}^{n}
{yi}i=0n,若函数集合
Φ
\Phi
Φ中函数
ϕ
(
x
)
\phi(x)
ϕ(x)满足条件
ϕ
(
x
i
)
=
y
i
(
i
=
0
,
1
,
2
,
⋯
,
n
)
\phi\left(x_{i}\right)=y_{i} \quad(i=0,1,2, \cdots, n)
ϕ(xi)=yi(i=0,1,2,⋯,n)
称
ϕ
(
x
)
\phi(x)
ϕ(x)为
f
(
x
)
f(x)
f(x)在
Φ
\Phi
Φ中关于节点
{
x
i
}
i
=
0
n
\{{x_i}\}_{i=0}^{n}
{xi}i=0n的插值函数。
R n ( x ) = f ( x ) − ϕ ( x ) R_{n}(x)=f(x)-\phi(x) Rn(x)=f(x)−ϕ(x)为插值余项。
选取
1
,
x
,
x
2
,
.
.
.
,
x
n
1,x,x^2,...,x^n
1,x,x2,...,xn作为n次多项式空间的一组基函数,对于多项式插值,有
R
n
(
x
)
=
f
(
x
)
−
ϕ
(
x
)
=
f
(
n
+
1
)
(
ξ
)
(
n
+
1
)
!
ω
n
+
1
(
x
)
R_{n}(x)=f(x)-\phi(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!} \omega_{n+1}(x)
Rn(x)=f(x)−ϕ(x)=(n+1)!f(n+1)(ξ)ωn+1(x)
其中
ξ
=
ξ
(
x
)
∈
(
a
,
b
)
,
ω
n
+
1
(
x
)
=
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
)
\xi=\xi(x) \in(a, b), \omega_{n+1}(x)=\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n}\right)
ξ=ξ(x)∈(a,b),ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)
Lagrange插值
线性插值
过两点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)的直线的方程为
y − y 0 = y 1 − y 0 x 1 − x 0 ( x − x 0 ) y - y_0 =\frac{y_1 - y_0}{x_1 - x_0}( x - x_0 ) y−y0=x1−x0y1−y0(x−x0)
整理可得,
y = x − x 1 x 0 − x 1 y 0 + x − x 0 x 1 − x 0 y 1 y =\frac{x - x_1}{x_0 - x_1}y_0 + \frac{x - x_0}{x_1 - x_0}y_1 y=x0−x1x−x1y0+x1−x0x−x0y1
引入记号,
l 0 ( x ) = x − x 1 x 0 − x 1 , l 1 ( x ) = x − x 0 x 1 − x 0 l_0( x )=\frac{x - x_1}{x_0 - x_1},\quad l_1( x )=\frac{x - x_0}{x_1 - x_0} l0(x)=x0−x1x−x1,l1(x)=x1−x0x−x0
易知 l 0 l_0 l0和 l 1 l_1 l1线性无关,
则有 L 1 ( x ) = l 0 ( x ) y 0 + l 1 ( x ) y 1 L_1( x ) = l_0( x ) y_0 + l_1( x ) y_1 L1(x)=l0(x)y0+l1(x)y1为Lagrange插值多项式。
对于二次多项式,可写出
L 2 ( x ) = l 0 ( x ) y 0 + l 1 ( x ) y 1 + l 2 ( x ) y 2 L_2( x ) = l_0( x ) y_0 + l_1( x ) y_1 + l_2( x ) y_2 L2(x)=l0(x)y0+l1(x)y1+l2(x)y2
需满足条件,
( l 0 ( x 0 ) = 1 l 0 ( x 1 ) = 0 l 0 ( x 2 ) = 0 ) \left( \begin{matrix}l_0( x_0 ) = 1 \\l_0( x_1 ) = 0 \\l_0( x_2 ) = 0 \end{matrix}\right) l0(x0)=1l0(x1)=0l0(x2)=0
( l 1 ( x 0 ) = 0 l 1 ( x 1 ) = 1 l 1 ( x 2 ) = 0 ) \left(\begin{matrix}l_1( x_0 ) = 0 \\l_1( x_1 ) = 1 \\l_1( x_2 ) = 0 \end{matrix}\right) l1(x0)=0l1(x1)=1l1(x2)=0
( l 2 ( x 0 ) = 0 l 2 ( x 1 ) = 0 l 2 ( x 2 ) = 1 ) \left(\begin{matrix}l_2( x_0 ) = 0 \\l_2( x_1 ) = 0 \\l_2( x_2 ) = 1 \end{matrix}\right) l2(x0)=0l2(x1)=0l2(x2)=1
对于n+1个节点的情形,
L
n
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
+
l
2
(
x
)
y
2
+
⋯
+
l
n
(
x
)
y
n
=
∑
i
=
0
n
l
i
(
x
)
y
i
L_n( x ) = l_0( x ) y_0 + l_1( x ) y_1 + l_2( x ) y_2 + \cdots + l_n( x ) y_n = \sum_{i = 0}^n l_i( x ) y_i
Ln(x)=l0(x)y0+l1(x)y1+l2(x)y2+⋯+ln(x)yn=i=0∑nli(x)yi
满足条件,
l
i
(
x
j
)
=
{
1
,
j
=
i
,
0
,
0
⩽
j
⩽
n
,
j
≠
i
,
l_i( x_j ) = \left\{\begin{matrix}1 ,& j = i ,\\0 ,& 0 \leqslant j \leqslant n ,j \neq i ,\end{matrix}\right.
li(xj)={1,0,j=i,0⩽j⩽n,j=i,
l
i
(
x
)
l_i(x)
li(x)为
l
i
(
x
)
=
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
i
−
1
)
(
x
−
x
i
+
1
)
⋯
(
x
−
x
n
)
(
x
i
−
x
0
)
(
x
i
−
x
1
)
⋯
(
x
i
−
x
i
−
1
)
(
x
i
−
x
i
+
1
)
⋯
(
x
i
−
x
n
)
.
l_i( x )=\frac{( x - x_0 ) ( x - x_1 )\cdots( x - x_{i-1} ) ( x - x_{i+1} )\cdots( x - x_n )}{( x_i - x_0 ) ( x_i - x_1 )\cdots( x_i - x_{i-1} ) ( x_i - x_{i+1} )\cdots( x_i - x_n )}.
li(x)=(xi−x0)(xi−x1)⋯(xi−xi−1)(xi−xi+1)⋯(xi−xn)(x−x0)(x−x1)⋯(x−xi−1)(x−xi+1)⋯(x−xn).
Newton插值法
过两点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)和 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)的直线方程记为
p 1 ( x ) = y 0 + y 1 − y 0 x 1 − x 0 ( x − x 0 ) = y 0 + c 1 ( x − x 0 ) . p_1( x ) = y_0 + \frac{y_1 - y_0}{x_1 - x_0}( x - x_0 ) = y_0 + c_1( x - x_0 ) . p1(x)=y0+x1−x0y1−y0(x−x0)=y0+c1(x−x0).
增加一个节点,
p 2 ( x ) = p 1 ( x ) + c 2 ( x − x 0 ) ( x − x 1 ) . p_2( x )=p_1( x ) + c_2( x - x_0 ) ( x - x_1 ) . p2(x)=p1(x)+c2(x−x0)(x−x1).
节点由k个增加到k+1个,满足
p k ( x ) = p k − 1 ( x ) + c k ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x k − 1 ) . p_k( x )=p_{k-1}( x ) + c_k( x - x_0 ) ( x - x_1 )\cdots( x - x_{k-1} ) . pk(x)=pk−1(x)+ck(x−x0)(x−x1)⋯(x−xk−1).
由此可得,
p
k
(
x
)
=
y
0
+
c
1
(
x
−
x
0
)
+
⋯
+
c
k
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
k
−
1
)
.
p_{k}( x )=y_{0}+c_{1}( x-x_{0} )+\cdots+c_{k}( x-x_{0} ) ( x-x_{1} )\cdots( x-x_{k-1} ) .
pk(x)=y0+c1(x−x0)+⋯+ck(x−x0)(x−x1)⋯(x−xk−1).
是以
1
,
x
−
x
0
,
(
x
−
x
0
)
(
x
−
x
1
)
,
⋯
,
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
k
−
1
)
1,x-x_0,(x-x_0)(x-x_1),\cdots,(x-x_0)(x-x_1)\cdots(x-x_{k-1})
1,x−x0,(x−x0)(x−x1),⋯,(x−x0)(x−x1)⋯(x−xk−1)为基函数的插值多项式,这种方法被称为Newton插值法。
分段线性插值
高次多项式插值是不稳定的。

三次样条插值