下面的内容为大家讲解关于非线性回归的内容，下面先带着大家回顾一下回归方程

回归方程

• 利用样本数据建立因变量(预报量)与一个或者多个自变量(预报因子)之间的统计关系经验方程式(回归方程)，用以描述预报量随自变量的平均变化情况，并据此对于预报量未来状态进行估计。

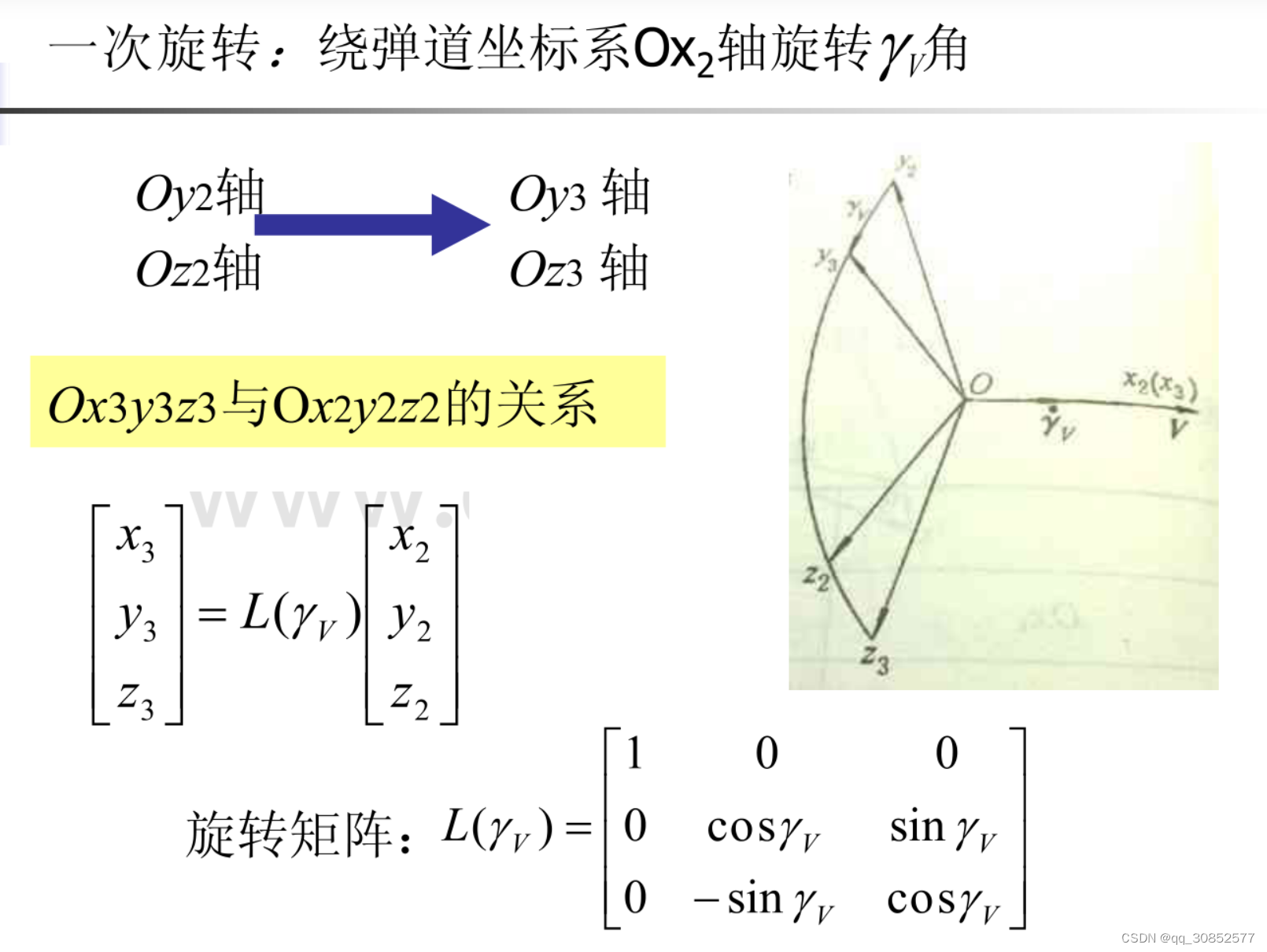
其中，根据预报因子的数量可以划分为一元回归和多元回归；进一步又可以划分为线性回归与非线性回归

线性回归

一元线性回归的关键：

• 确定回归方程 / 确定回归系数

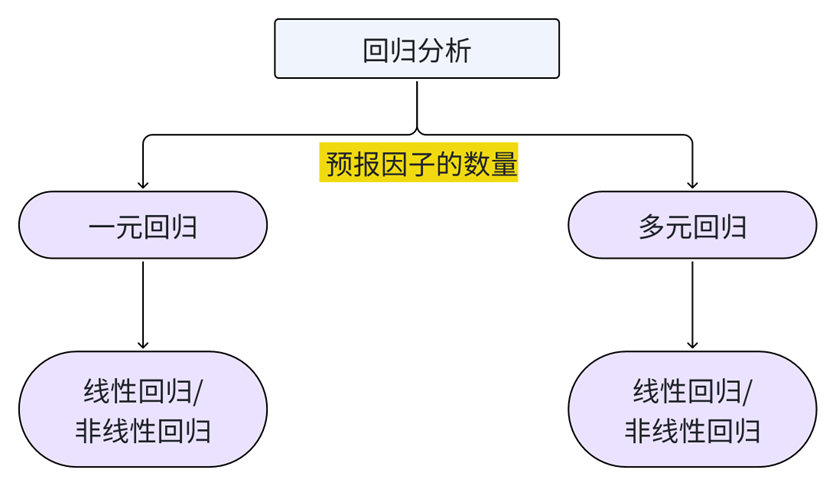
一元线性回归方程通常表现形式

• 预报量的估计量 = 回归系数a + 回归系数b*预报因子

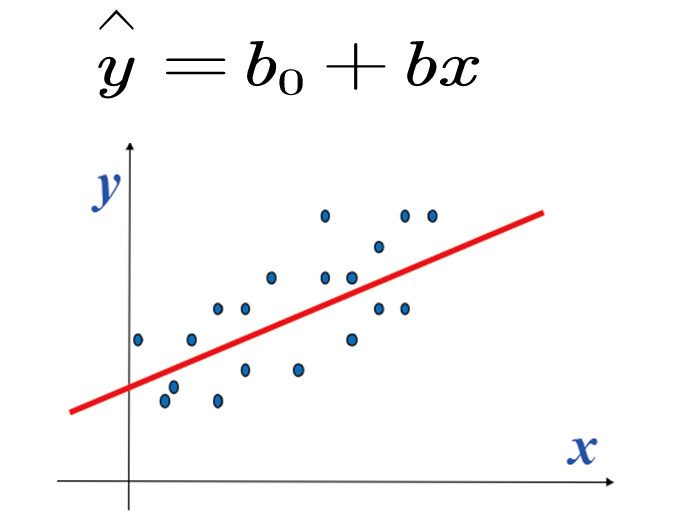
如何确定回归系数

主要取决于以下两点：

• 回归系数应该对于y的估计值与y观测值的总的偏差尽可能小

• 使用偏差平方来反映绝对偏差的情况，消除偏差符号的影响

即

$$\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2\text{达到最小值}$$

如何理解呢？$\hat{y}$是什么呢，请看下面这张图：

所以实际上就是计算观测值$y$与估计值$\hat{y}$之间偏差平方和的最小值,即残差平方和，表现为：

$$Q\equiv \sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2=\sum _{i=1}^n{\left(y_i-b_0-b{x}_i\right)}^2\to min$$

要使得Q最小，根据高数极值原理，其必要条件为：

$$\{\begin{array}{l}\frac{\partial Q}{\partial b_0}=0\\ \frac{\partial Q}{\partial b}=0\end{array}⟶\{\begin{array}{l}-2{\sum }_{i=1}^n\left(y_i-b_0-b{x}_i\right)=0\\ -2{\sum }_{i=1}^n\left(y_i-b_0-b{x}_i\right)x_i=0\end{array}$$

也就是说对于他的回归系数分别求偏导，具体的求解过程我会写在黑板上。下面直接给出结果：

$$b=\frac{s_{xy}}{s_x^2}$$
$$b_0=\bar{y}-b\bar{x}$$

其中，

$$\bar{x}=\frac{1}{n}\sum _{i=1}^n{x}_i;\bar{y}=\frac{1}{n}\sum _{i=1}^n{y}_i$$

$$s_x^2=\frac{1}{n}\sum _{i=1}^n{\left(x_i-\bar{x}\right)}^2;s_{xy}=\frac{1}{n}\sum _{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)$$

这样就得到了回归系数的表达结果，那么，以上以预报因子x预报得到的$\hat{y}$,仅仅是一个估计值，如何评估其与真值之间的差别呢？

可以根据方差来评估，即：

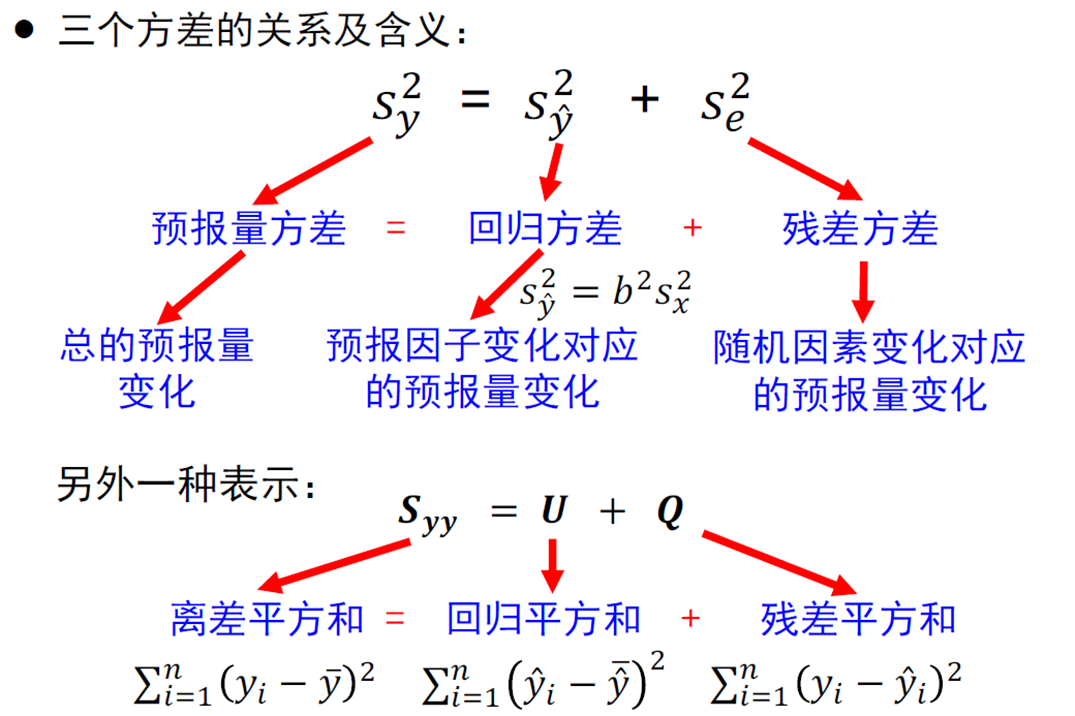
预报量的方差 = 回归估计值的方差 + 误差方差

三个方差的关系以及含义，如下所示，每一项的具体推导这里我也会在黑板上演示

对于回归方差来说，$S_{\hat{y}}^2$ 越大，残差$S_e^2$越小，回归效果越好；为了便于不同变量回归效果的比较，可以定义无量纲回归效果指数，即解释方差，又称为判决系数

$$R^2=\frac{s_{\hat{y}}^2}{s_y^2}$$

$R^2$越大，回归效果越好，表示两者之间的关系越密切。

$$R^2=\frac{s_{\hat{y}}^2}{s_y^2}=\frac{b^2{s}_x^2}{s_y^2}=\frac{s_{xy}}{s_x^2}\frac{s_{xy}}{s_x^2}\frac{s_x^2}{s_y^2}=r^2$$

此外，解释方差相当于相关系数的平方，回归效果取决于相关系数平方的大小。

示例演示

下面找两个图来演示回归的作用

其实现回归的方法如下：

• 将未滤波的变量通过线性回归的方法投影到EOF第一模态的PC时间序列上，重建三维波列结构

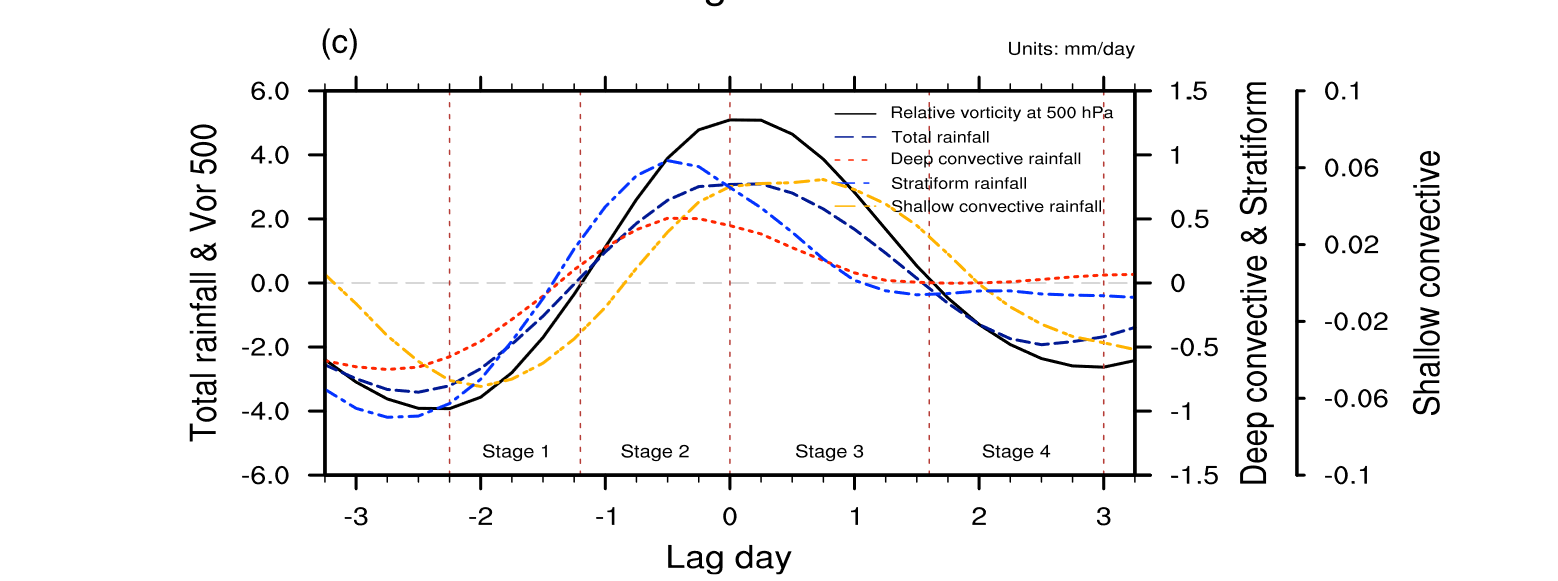
上图显示了回归得到500 h Pa 相对涡度、总雨强、深对流雨强、浅对流雨强、层云雨强的时间序列，结果表明：深对流和层云降水事件与500 h Pa相对涡度几乎同步发生，浅对流降水发生在最深对流之后

• 回归高度-时间图：( a )经向风，( b )温度，( c )散度，( d )比湿。

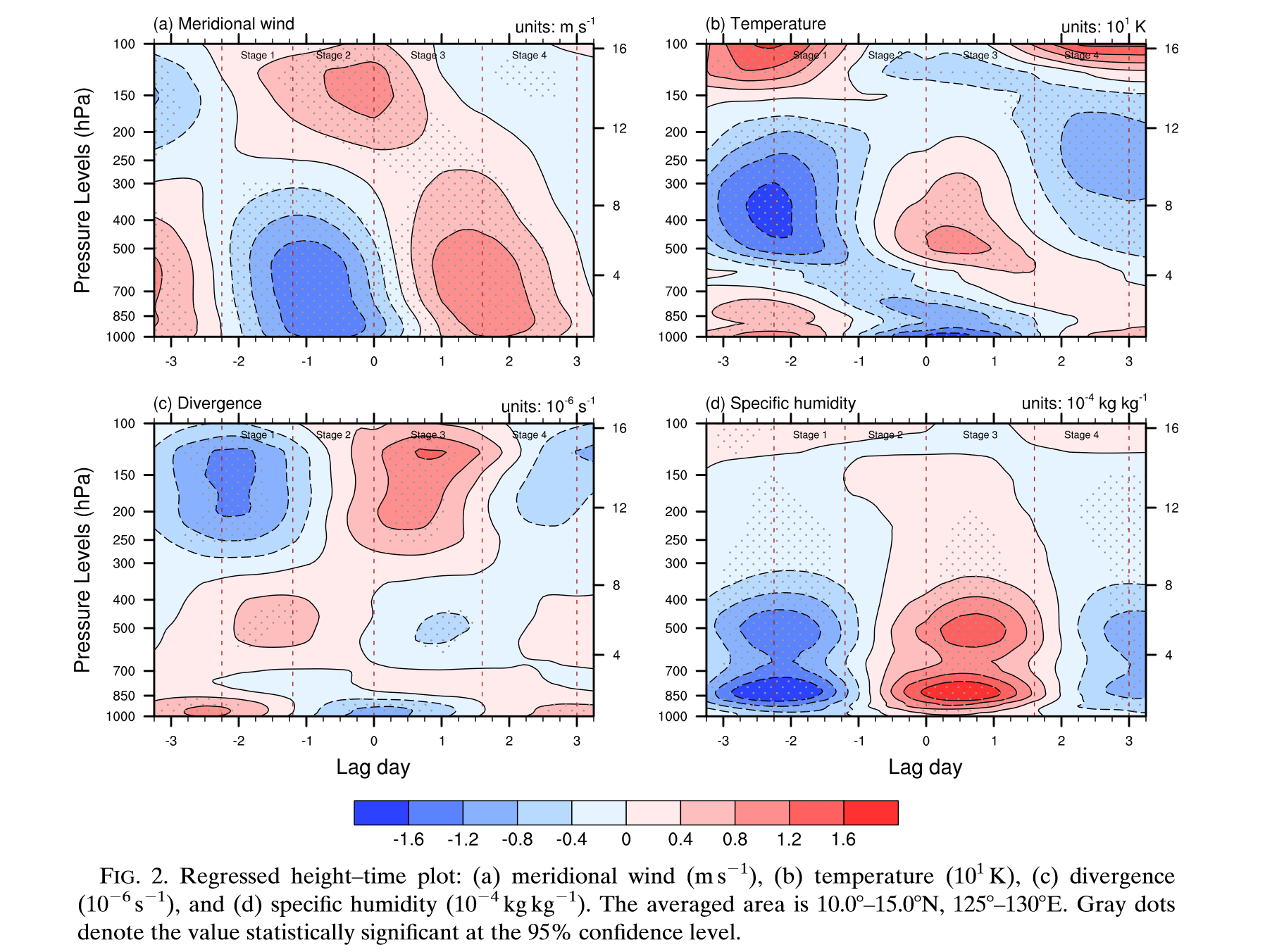
回归得到的TD波结构显示如下特征：

• 包括扰动中心前部中层辐散、中心附近低层辐合叠加高层辐散、温度异常中存在垂直偶极子结构、波中心附近对流层中低层水汽增强。

---

多元线性回归

多元线性回归是指，对于一个预报量$y$，研究多个预报因子(假如有$p$个因子)，𝑥_1,𝑥_2…,𝑥_𝑝与它的线性统计关系，第𝑖次观测的因子值（𝑛个随机变量）为𝑥_{𝑖1},𝑥_{𝑖2},⋯,𝑥_{𝑖𝑝},参考一元线性回归的表示式，可以得到以下形式:

$$\begin{array}{rl}{y}_1& ={\beta }_0+{\beta }_1{x}_{11}+{\beta }_2{x}_{12}+\cdots +{\beta }_p{x}_{1p}+e_1\\ y_2& ={\beta }_0+{\beta }_1{x}_{21}+{\beta }_2{x}_{22}+\cdots +{\beta }_p{x}_{2p}+e_2\\ ...& \\ y_p& ={\beta }_0+{\beta }_1{x}_{n1}+{\beta }_2{x}_{n2}+\cdots +{\beta }_p{x}_{np}+e_n\end{array}$$

其中，$\beta$为估计参数，$e$为残差，残差互相独立，可以将其写为矩阵形式

$$y=X\beta +e$$

$$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],\mathbf{\beta }=\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_p\end{array}\right],\mathbf{e}=\left[\begin{array}{c}{e}_1\\ e_2\\ ⋮\\ e_n\end{array}\right]$$

$X$ 为因子矩阵，阵中多引入一个常数变量𝑥_0，其数值为1，即

$$\mathbf{X}=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_p\\ 1& x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& ⋮& & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]$$

进行估计，得到估计的多元线性回归方程，𝑏_0,𝑏_1,𝑏_2…,𝑏_𝑝 是 𝛽_0,𝛽_1,𝛽_2…,𝛽_𝑝 的估计，

$$\hat{y}=b_0+b_1{x}_1+b_2{x}_2+\cdots +b_p{x}_p$$
也可以表现为矩阵的形式：
$$\hat{y}=Xb$$

其中，

$$

\hat{y}=\left[ \begin{array}{c}
\hat{y}1\
\hat{y}2\
\vdots\
\hat{y}n\
\end{array} \right]
，
\boldsymbol{X}=\left[ \begin{matrix}
1& x{11}& x{12}& \cdots& x_p\
1& x{21}& x_{22}& \cdots& x_{2p}\
\vdots& \vdots& \vdots& & \vdots\
1& x_{n1}& x_{n2}& \cdots& x_{np}\
\end{matrix} \right]

，

b=\left[ \begin{array}{c}
b_0\
b_1\
\vdots\
b_p\
\end{array} \right]

$$

• 多元线性回归方程的矩阵形式，𝑋 为因子矩阵，𝑏为回归系数向量

如何确定估计参数呢？

• 和之前一元线性回归类似，使得全部的预报量观测值和回归估计值的差值平方和达到最小

$$Q=\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2⟶\text{最小}$$

$$
y=X\beta +e
,

\hat{y}=Xb

,

\text{残差}e\ =\ y-\hat{y}=y-Xb
$$

最小二乘法的目标是最小化残差平方和，即$\lVert e^2 \rVert \ $,最小化，表示为残差的范数的平方和

所以，优化问题为$\underset{b}{\min }\Vert y-Xb{\Vert }^2$

可以通过求解正规方程来找到参数$b$的最佳估计值,

$$X^{T}Xb=X^{T}y$$

当然，这么直接得到上面的正规方程有点跨越太大，这里做出展开推导：

• 预报量观测向量与回归估计向量之差的内积即它们的分量的差值平方和

所以，
$$Q=(y-\hat{y}{)}^{\prime }(y-\hat{y})=(y-Xb{)}^{\prime }(y-Xb)=y^{\prime }y-b^{\prime }{X}^{\prime }y-y^{\prime }Xb+b^{\prime }{X}^{\prime }Xb$$

Q为非负二次式，最小值存在，由微分极值原理，有：

$$\frac{\partial Q}{\partial b}=\frac{\partial (y^{\prime }y)}{\partial b}-\frac{\partial (b^{\prime }{X}^{\prime }y)}{\partial b}-\frac{\partial (y^{\prime }Xb)}{\partial b}+\frac{\partial (b^{\prime }{X}^{\prime }Xb)}{\partial b}=0$$

其中，等号右边第一项不是b的函数，偏微分为0
第二、第三项有：
$$\frac{\partial ({\mathbf{b}}^{\prime }{\mathbf{X}}^{\prime }\mathbf{y})}{\partial \mathbf{b}}={\mathbf{X}}^{\prime }\mathbf{y}$$

第四项为：
$$\frac{\partial \left(b^{\prime }{X}^{\prime }Xb\right)}{\partial b}=2X^{\prime }Xb,\text{所以}\frac{\partial Q}{\partial b}=2X^{\prime }Xb-2X^{\prime }y=0,\text{即得}$$

整理可得：

$$X^{T}Xb=X^{T}y$$

其中$X^{\prime }X$称为标准方程组系数矩阵，展开为：
$$\{\begin{array}{l}n{b}_0+b_1{\sum }_{i=1}^n{x}_{i1}+\cdots +b_p{\sum }_{i=1}^n{x}_{ip}={\sum }_{i=1}^n{y}_i\\ b_0{\sum }_{i=1}^n{x}_{i1}+b_1{\sum }_{i=1}^n{x}_{ip}^2+\cdots +b_p{\sum }_{i=1}^n{x}_{i1}{x}_{ip}={\sum }_{i=1}^n{x}_{i1}{y}_i\\ ............\\ b_0{\sum }_{i=1}^n{x}_{ip}+b_1{\sum }_{i=1}^n{x}_{ip}{x}_{i1}+\cdots +b_p{\sum }_{i=1}^n{x}_{ip}^2={\sum }_{i=1}^n{x}_{ip}{y}_i\end{array}$$

向量b(回归系数解)，即为参数β的最小二乘估计:

$$b=X^{\prime }{X}^{-1}{X}^{\prime }y$$

同理得到：

三个平方和的关系为：

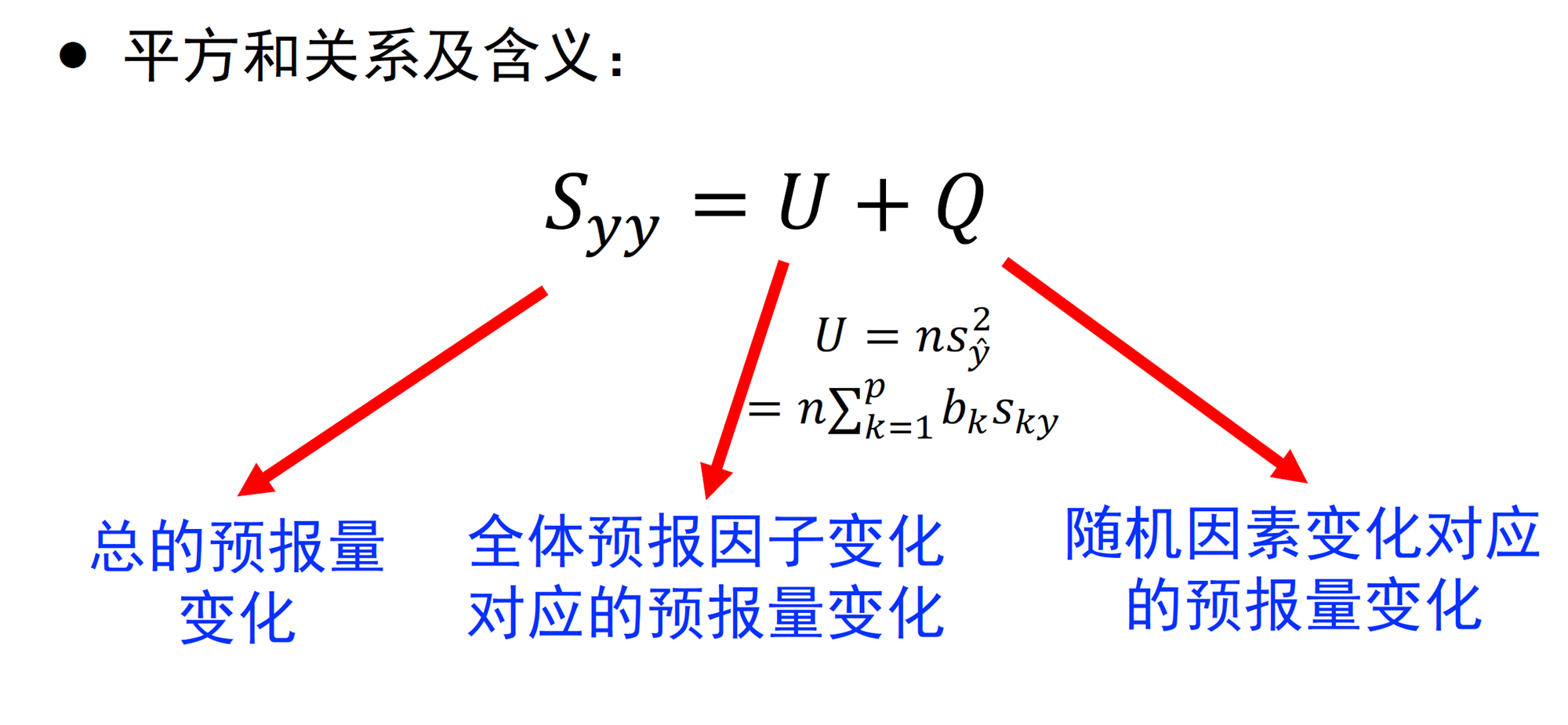
• 解释方差为：

$$R^2=\frac{U}{S_{yy}}=1-\frac{Q}{S_{yy}}$$

$R^2$表示全体预报因子所能解释的预报量方程百分比，取值范围为[0,1]，$R^2$越大越好

非线性回归

定义

• 非线性回归生成一个用于描述连续响应变量与一个或多个预测变量之间的非线性关系的方程，并预测新观测值。

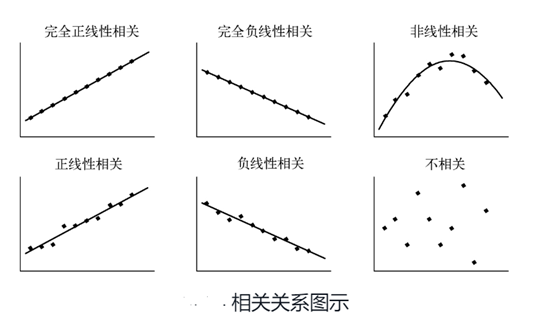
如果两个变量之间的关系不是线性的，则上升速率或下降速率可能会随着一个变量变化而变化，这会导致数据中出现“曲线模式”。

下面是简单的示意图;

非线性回归模型一般形式

$$y_i=f\left({\mathbf{x}}_{\mathbf{i}},\mathbf{\gamma }\right)+e_i$$

其中，

${\mathbf{x}}_{\mathbf{i}}$ 为含p个因子变量的第i个样品向量，$\mathbf{\gamma }$为非线性回归系数向量，$e_i$为误差

$
y_i
$
为第i个样品的预报量，$ f(\boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{\gamma })$ 为${\mathbf{x}}_{\mathbf{i}}$的任意非线性函数

使用高斯-牛顿方法来确定非线性回归系数向量，对${\mathbf{x}}_{\mathbf{i}}$及$\mathbf{\gamma }$的非线性函数

$f( \boldsymbol{x}_{\boldsymbol{i}},\boldsymbol{\gamma}) $

在回归系数$p+1$维空间中任一点${\mathbf{\gamma }}^{(0)}$ 附近邻域做泰勒展开

$$f\left(x_i,\gamma \right)\cong f\left(x_i,\gamma \right)+\sum _{k=0}^p{\left[\frac{\partial f\left(x_i,\gamma \right)}{\partial {\gamma }_k}\right]}_{\gamma -{\gamma }^{\left(0\right)}}\cdot \left(\gamma -{\gamma }^{\left(0\right)}\right)$$

式中，

$${\gamma }^{\left(0\right)}=\left[\begin{array}{c}{\gamma }_0^{\left(0\right)}\\ {\gamma }_1^{\left(0\right)}\\ ⋮\\ {\gamma }_p^{\left(0\right)}\end{array}\right]$$

为了方便说明，这里令

$$\{\begin{array}{l}{f}_i^{\left(0\right)}=f\left({\mathbf{x}}_i,{\mathbf{\gamma }}^{\left(0\right)}\right)\\ {\beta }_k^{\left(0\right)}={\mathbf{\gamma }}_k-{\mathbf{\gamma }}_k^{\left(0\right)}\\ D_{ik}^{\left(0\right)}={\left[\frac{\partial f\left({\mathbf{x}}_i,\mathbf{\gamma }\right)}{\partial {\mathbf{\gamma }}_k}\right]}_{\gamma -{\mathbf{\gamma }}^{\left(0\right)}}\end{array}$$

则非线性函数的泰勒展开表示为：

$$f\left(x_i,\gamma \right)\cong f_i^{\left(0\right)}+\sum _{k=0}^p{D}_{ik}^{\left(0\right)}{\beta }_k^{\left(0\right)}$$

将其带入

$$y_i=f\left(x_i,y\right)+e_i$$

得到：

$$y_i=f_i^{\left(0\right)}+\sum _{k=0}^p{D}_{ik}^{\left(0\right)}{\beta }_k^{\left(0\right)}+e_i$$

若令
$$y_i^{\left(0\right)}=y_i-f_i^{\left(0\right)}$$
上式变为：

$$y_i^{\left(0\right)}=\sum _{k=1}^p{D}_{ik}^{\left(0\right)}{\beta }_k^{\left(0\right)}+e_i$$

即一般的非线性回归模型，这是可以把

$$D_k^{\left(0\right)}\left(k=0,1,\cdots ,p\right)$$

看作是P+1 个变量，于是回归系数向量${\beta }_{\left(0\right)}$的估计值容易用计算多元线性回归的方法求解

---

简单理解

当然，上面的推导过程看起来有点抽象，我下面换个容易看懂的方式。

如下面的非线性回归模型，表示为

$$

y = f(X,\beta)+\epsilon

$$

其中，$\beta$为回归系数，$ϵ$为误差，为了求解上述模型，可以通过求解最小二乘估计量(极大似然估计量)的方法，即将期望函数线性化，然后利用Gauss-Newton迭代法进行求解。

Gauss-Newton法的步骤为：

• 1、选定初始值
  • 1.1 根据经验给出
  • 1.2 用分段法给出初始值
  • 1.3 对于可线性化的非线性模型，通过线性化，然后使用最小平方法求解初始值
• 2、 使用泰勒展开式

那么，针对上面的回归模型，如何进行泰勒展开呢？

• 在数学上，对于一个在实数或复数𝑎邻域上，以实数作为变量或以复数作为变量的函数，并且是无穷可微的函数𝑓(𝑥)，它的泰勒级数是以下这种形式的幂级数：

$$\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

对于$y=f(x,\beta )+ϵ$，在$\beta =b_0$处进行泰勒展开，忽略二次想:

$$y=f\left(X,\beta \right)+ϵ=f\left(X,b_0\right)+\frac{\partial f\left(X,\beta \right)}{\partial {\beta }^{\mathrm{T}}}(\beta -b_0)+ϵ$$

进行如下假设：

$$y_0=y-f\left(X,b_0\right)=y-f_0\text{,}{\theta }_0=\beta -b_0\text{,}{D}_0={\left[\frac{\partial f(X,\beta )}{\partial {\beta }^{\mathrm{T}}}\right]}_{\beta =b_0}$$

那么，得到：

$$y_0=D_0{\theta }_0+ϵ$$

如果将其看作是矩阵的话，就和上面的推导结果一致了。

求解回归系数

所以${\theta }_0$的最小二乘估计量为，

$$\begin{array}{rl}{\hat{\theta }}_0& ={\left(D_0^{\mathrm{T}}{D}_0\right)}^{-1}{D}_0^{\mathrm{T}}{y}_0\\ & ={\left(D_0^{\mathrm{T}}{D}_0\right)}^{-1}{D}_0^{\mathrm{T}}\left(y-f_0\right)\end{array}$$

• 这和之前多元线性回归方程中通过求解正规方程来找到参数$b$的最佳估计值的方法类似,

因为${\theta }_0=\beta -b_0$,那么用$b_1 = b_0 +\hat{\theta}_{0} $ 作为未知参数$\beta$的一个修正估计，按照此逻辑不断迭代修正$\beta$

即：

$$\begin{array}{rl}{b}_{k+1}& =b_k+{\hat{\theta }}_k\\ & =b_k+{\left(D_k^{\mathrm{T}}{D}_k\right)}^{-1}{D}_k^{\mathrm{T}}\left(y-f_k\right)\end{array}$$

当这种修正满足收敛条件时，或者是前后两个估计的改变很小时，即
$$\frac{\Vert b_{k+1}-b_k\Vert }{\Vert b_k\Vert }<\delta$$

迭代结束，其中，$\delta$是一个迭代终止的条件，一个很小的数。这也是梯度下降的原理，在深度学习中得到广泛应用，稍后在深度学习中的讲解中会更好的理解。

非线性回归系数计算

一般求非线性回归系数可以用迭代法求出，步骤如下：

• 给定回归系数向量，${\hat{\gamma }}^{\left(0\right)}$一个初值

• 根据非线性函数求出:$f_i^{\left(0\right)}\left(i=1,2,\cdots ,n\right)$

• 根据$D_i{k}^{\left(0\right)}={\left[\frac{\partial f\left(x_i,\gamma \right)}{\partial {\gamma }_k}\right]}_{\gamma -{\gamma }^{\left(0\right)}}:D_i{k}^{\left(0\right)}\left(k=0,1,2,\cdots ,p\right)$

• 根据$y_i^{\left(0\right)}=y_i-f_i^{\left(0\right)}$ 求出：$y_i^{\left(0\right)}$

• 根据回归方程$y_i^{\left(0\right)}={\sum }_{k=1}^p{D}_{\text{ik}}^{\left(0\right)}{\beta }_k^{\left(0\right)}+e_i$ 计算得到线性回归系数估计。${\hat{\beta }}_k^{\left(0\right)},\left(k=0,1,2,\cdots ,p\right)$

• 通过${\beta }_k^{\left(0\right)}$ 求出下一次回归系数的估计：${\hat{\gamma }}_k^{\left(1\right)}={\hat{\gamma }}_k^{\left(0\right)}={\hat{\beta }}_k^{\left(0\right)},\left(k=0,1,\cdots ,p\right)$

• 计算残差平方和

对于非线性回归残差平方和仍表示为：

$$Q=\sum _{i=1}^n{\left(y_i-f\left(x_i,\hat{\gamma }\right)\right)}^2$$

一开始的残差平方和可表示为：

$Q^{\left(0\right)}={\sum }_{k=1}^p{\left(y_i-f_i^{\left(0\right)}\right)}^2$

类似的，下一步的残差平方和表示为：

$$Q^{\left(1\right)}=\sum _{i=1}^n{\left(y_i-f_i\left(x_i,{\hat{\mathbf{\gamma }}}^{\left(1\right)}\right)\right)}^2=\sum _{i=1}^n{\left(y_i-f_i^{\left(1\right)}\right)}^2$$
此时，对于$Q^{\left(1\right)}$进行判断，
如果$Q^{\left(1\right)}-Q^{\left(0\right)}$不够小，回到2继续过程,求出.$Q^{\left(2\right)},...,Q^{\left(3\right)}$进行判断
直到绝对值达到拟合精度，迭代结果后的${\hat{\gamma }}_k^{\left(3\right)}$为最后的非线性回归系数，复相关系数表示为：

$$R^2=\frac{S_{yy}-Q^{\left(s\right)}}{S_{yy}}$$

• 一些非线性函数，可以变化转化为线性函数，因此，曲线回归问题可以用线性回归进行处理

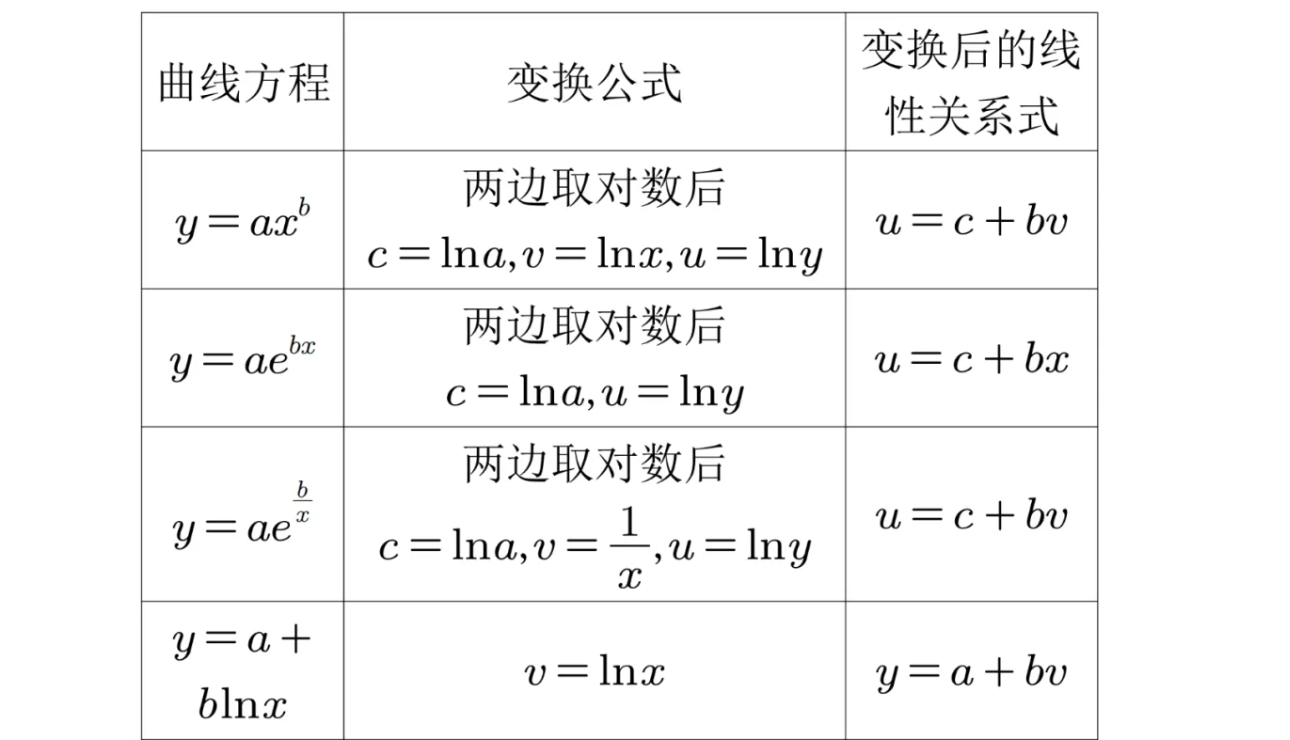
总结

• 掌握一元线性回归的推导
• 熟悉多元线性回归求解的方法
• 理解非线性回归的意义与一般表现形式
• 通过非线性回归方程的推导建立于深度学习方法的联系

泰勒级数：https://zh.wikipedia.org/wiki/%E6%B3%B0%E5%8B%92%E7%BA%A7%E6%95%B0

最小二乘法：https://zh.wikipedia.org/wiki/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95

高斯-牛顿迭代：https://baike.baidu.com/item/%E9%AB%98%E6%96%AF%E2%80%94%E7%89%9B%E9%A1%BF%E8%BF%AD%E4%BB%A3%E6%B3%95/15667583

回归示例图片来源：Feng, T., J. Yu, X. Yang, and R. Huang, 2020: Convective Coupling in Tropical-Depression-Type Waves. Part II: Moisture and Moist Static Energy Budgets. J. Atmos. Sci., 77, 3423–3440, https://doi.org/10.1175/JAS-D-19-0173.1.