图形学初识--空间变换

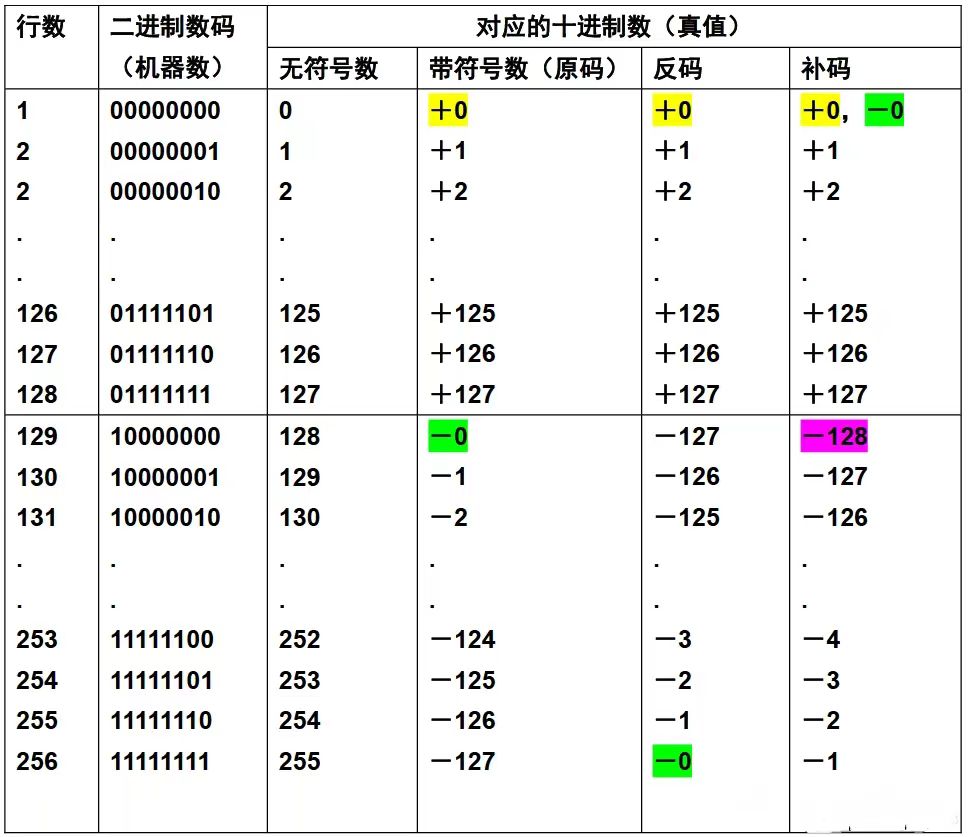
文章目录

前言
正文
- 矩阵和向量相乘
- 二维变换
- - 1、缩放
  - 2、旋转
  - 3、平移
  - 4、齐次坐标下总结
- 三维变换
- - 1、缩放
  - 2、平移
  - 3、旋转
  - - 绕X轴旋转：
    - 绕Z轴旋转：
    - 绕Y轴旋转：
结尾：喜欢的小伙伴可以点点关注+赞哦

前言

前面章节补充了一下基本的线性代数中关于向量和矩阵的背景知识，这一节咱们讲解一下在二维和三维中常用的空间变换，主要包括：平移、旋转、缩放等！

正文

矩阵和向量相乘

假设有一个矩阵 $M$ ，有一个向量 $\begin{pmatrix} x\\y \end{pmatrix}$ ，则令 $\vec P' = M \times \vec P = \begin{pmatrix} x'\\y' \end{pmatrix}$ .

从上节，我们已经知道矩阵和向量相乘结果还是个向量，假设我们把向量 $P$ 看作一个坐标，那么 $P^{'}$ 的坐标就是矩阵 $M$ 应用之后的结果，此时我们称对点 $P$ 应用矩阵 $M$ 的变换。

二维变换

假设在二维空间下，矩阵 $M$ 是2x2的，向量 $\begin{pmatrix} x\\y \end{pmatrix}$ 是二维向量。

矩阵乘向量在二维空间本质理解： 假设我们将 $M$ 按照列方向，分解成两个列向量 $(\vec{\alpha_1}, \vec{\alpha_2})$ ，则 $\vec{P'} = (x\vec{\alpha_1} + y\vec{\alpha_2})$

结果表明： 矩阵和向量相乘，就相当于向量的轴分量作为权重，给矩阵的列向量加权求和！

类似的，我们也可以把矩阵按照行向量分解，也可以表达成矩阵的行向量加权相加的形式。只不过列向量分解形式更为常见！

1、缩放

缩放矩阵M如下， $S_x$ 为x轴向的缩放因子， $S_y$ 为y轴向的缩放因子。
$\begin{bmatrix} s_x & 0\\ 0 & s_y\\ \end{bmatrix}$
则 $\begin{bmatrix} s_x & 0\\ 0 & s_y\\ \end{bmatrix} * \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} s_x * x\\s_y * y \end{pmatrix}$

举个例子： $\begin{bmatrix} 0.5& 0\\ 0 & 0.5\\ \end{bmatrix}$ ， $\begin{pmatrix} 2\\2 \end{pmatrix}$ ，则 $\begin{pmatrix} 1\\1 \end{pmatrix}$ ，如下图所示：

在这里插入图片描述

2、旋转

默认地，正角度旋转代表逆时针，如下图所示的红色正方形，就是旋转45°

在这里插入图片描述

旋转矩阵 $R_\theta$ 如下：
$\begin{bmatrix} \cos \theta & -\sin \theta\\ \sin \theta & \cos \theta\\ \end{bmatrix}$

基本推导如下图：

在这里插入图片描述

我们使用最笨的待定系数法求解，将矩阵 $R_{\theta}$ 设为 $\begin{bmatrix} A & B\\ C & D\\ \end{bmatrix}$ ，然后将两个点的前后结果带入计算，如下：
$\begin{bmatrix} A & B\\ C & D\\ \end{bmatrix}\begin{pmatrix} 1\\0 \end{pmatrix} = \begin{pmatrix} \cos{\theta}\\\sin{\theta} \end{pmatrix}， \begin{bmatrix} A & B\\ C & D\\ \end{bmatrix}\begin{pmatrix} 0\\1 \end{pmatrix} => \begin{pmatrix} -\sin{\theta}\\\cos{\theta} \end{pmatrix}$
所以自然得到：
$\begin{align} A &= \cos \theta\\ B &= -\sin \theta\\ C &= \sin \theta\\ D &= cos \theta\\ \end{align}$

3、平移

平移就是让x轴和y轴的坐标分别偏移一定的量，如下图所示：

在这里插入图片描述

$x' = x + t_x\\ y' = y + t_y$

我们记 $\begin{pmatrix} x\\y \end{pmatrix}$ ， $\begin{pmatrix} x'\\y' \end{pmatrix}$ ， $\begin{pmatrix} t_x\\t_y \end{pmatrix}$ ，则上述可以表示为 $\vec{P'} = \vec P + \vec T$

但是我们发现，上述的形式没有用上矩阵，但在数学、物理中，人们都讲究统一，因此人们引入了齐次坐标的概念。

为了迎合平移也能统一使用矩阵进行变换，认为的给二维的向量添加一个维度，升为三维，如下：
$\begin{pmatrix} x\\y\\1 \end{pmatrix}，vector = \begin{pmatrix} x\\y\\0 \end{pmatrix}$
我们发现，位置向量咱们第三维补充1，方向向量咱们第三维补充0。

于是，咱们自然而然就可以定义出平移矩阵T，如下：
$\begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix}\\ 注：t_x 表示x轴的偏移量，t_y表示y轴的偏移量$
于是，针对位置点的平移、以及位置向量的平移计算结果如下：

在这里插入图片描述

我们发现，方向向量的结果没有变化，这难道出问题了么？并没有，因为方向向量本身就是位置无关的，不变才是对的，而针对某个顶点是变化了的，这就符合咱们的要求！

4、齐次坐标下总结

引入齐次坐标后，缩放和旋转矩阵多了一个维度，这里列举一下：

缩放矩阵：
$\begin{bmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{bmatrix}$
旋转矩阵：
$\begin{bmatrix} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0 & 0 & 1 \end{bmatrix}$

平移矩阵：
$\begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix}\\$

三维变换

首先，由于多引入了一个维度，复杂度上升。坐标系自然而然分为两种：左手系、右手系，示意图如下：

在这里插入图片描述

**为了方便，后续三维空间中的矩阵变换讲解以右手系为例！**左手系也是类似，大家熟练之后可自行推导！

同理，在三维坐标系下，同样为了统一平移的操作，引入齐次坐标后，变换矩阵都是4x4的，这里不多赘述！

1、缩放

由于缩放最是容易，也最容易理解，这里直接给出缩放矩阵：
$\begin{bmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ 注：s_x、s_y、s_z分别为x、y、z轴的缩放比例$

2、平移

也是类似，这里直接给出平移矩阵：
$\begin{bmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ 注：t_x、t_y、t_z分别为x、y、z轴的偏移量$

3、旋转

由于三维世界中，旋转并不是绕一个点，而是绕一个旋转轴，所以最简单的旋转就是绕：x、y、z轴的旋转。

旋转规则： 绕某个轴旋转 $\theta$ 角度，就是表明逆着此轴的方向眼睛看过去，逆时针旋转 $\theta$ 角度。

例如如下示意图就是绕z轴旋转 $\theta$ 角度：

在这里插入图片描述

并且我们一定要理解，绕z轴转动时，所有点的z坐标是不会变化的！

这里需要对照二维空间中的旋转矩阵的理解，本质上：二维旋转就是将两个相互垂直的基向量作为坐标轴，逆时针旋转的结果

所以，上述的绕z轴的旋转，可以理解为基向量就是 $\begin{pmatrix} 1\\0\\0 \end{pmatrix}$ 和 $\begin{pmatrix} 0\\1\\0 \end{pmatrix}$

这里给出一个基本任意正交基向量 $\vec{i}、\vec{j}$ 的旋转示意图：

在这里插入图片描述

绕X轴旋转：

示意图如下：

在这里插入图片描述

因此，我们只是将基向量变成 $\begin{pmatrix} 0\\1\\0 \end{pmatrix}$ 和 $\begin{pmatrix} 0\\0\\1 \end{pmatrix}$

所以，很容易构造出以下等式：
$\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos{\theta} & -\sin{\theta} & 0\\ 0 & \sin{\theta} & \cos{\theta} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \begin{pmatrix} x\\i\\j\\1 \end{pmatrix} =\begin{pmatrix} x\\\cos{\theta}*i - \sin{\theta} * j\\\sin{\theta}*i + \cos{\theta} * j\\1 \end{pmatrix}$

自然而然可以得出，绕x轴的旋转矩阵如下：
$R_x = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \cos{\theta} & -\sin{\theta} & 0\\ 0 & \sin{\theta} & \cos{\theta} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

绕Z轴旋转：

同理，示意图：

在这里插入图片描述

容易构造出以下等式：
$\begin{bmatrix} \cos{\theta} & -\sin{\theta} & 0 & 0\\ \sin{\theta} & \cos{\theta} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \begin{pmatrix} i\\j\\z\\1 \end{pmatrix} =\begin{pmatrix} \cos{\theta}*i - \sin{\theta} * j\\\sin{\theta}*i + \cos{\theta} * j\\z\\1 \end{pmatrix}$
自然而然可以得出，绕z轴的旋转矩阵如下：
$R_z = \begin{bmatrix} \cos{\theta} & -\sin{\theta} & 0 & 0\\ \sin{\theta} & \cos{\theta} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

绕Y轴旋转：

Y轴相比X和Z比较特殊，也是新手初学三维空间旋转最容易困惑的地方。但在咱们这里不存在，示意图如下：

在这里插入图片描述

容易构造出以下等式：
$\begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} & 0\\ 0 & 1 & 0 & 0\\ -\sin{\theta} & 0 & \cos{\theta} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \begin{pmatrix} j\\y\\i\\1 \end{pmatrix} =\begin{pmatrix} \sin{\theta}*i + \cos{\theta} * j\\y\\\cos{\theta}*i - \sin{\theta} * j\\1 \end{pmatrix}$
咱们发现，这里的形式稍微较绕x和绕z不一样了

本质就是因为这里的正交基分别是： $\begin{pmatrix} 0\\0\\1 \end{pmatrix}$ 和 $\begin{pmatrix} 1\\0\\0 \end{pmatrix}$

自然而然可以得出，绕y轴的旋转矩阵如下：
$R_y = \begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} & 0\\ 0 & 1 & 0 & 0\\ -\sin{\theta} & 0 & \cos{\theta} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$