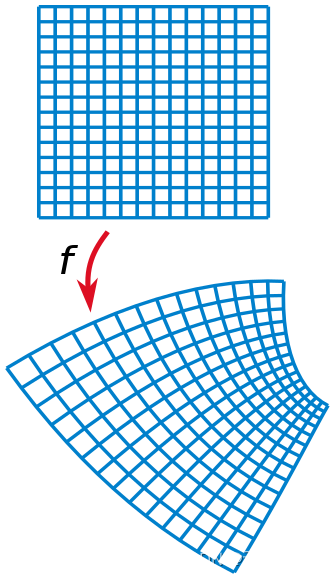
一、说明
关于莫比乌斯变换,是一个代数几何变换的重要概念。也是双曲几何的重要理论,比如庞加莱盘就是建立在这个理论上,那么这个变换到底有哪些内容?本文将做出详细的解读。
二、线性变换和逆变换
在本节中,我们研究莫比乌斯变换,它提供了找到一个域到的一对一映射的非常方便的方法。让我们从线性变换开始。
2.1 线性变换
w
=
φ
(
z
)
:
=
A
z
+
B
w = φ(z) := Az + B
w=φ(z):=Az+B
其中,其中 A 和 B 是固定复数,
A
≠
0
A \neq 0
A=0
w
=
φ
(
z
)
:
=
∣
A
∣
e
i
A
(
a
)
z
+
B
.
w = φ(z) := |A|e^{iA(a)}z + B.
w=φ(z):=∣A∣eiA(a)z+B.
正如我们所看到的,将变换分成三个部分:
1)一个变换是围绕原点经过一次旋转,旋转角度 Arg (a).
w
1
:
=
e
i
A
r
g
(
a
)
z
w1 := e^{iArg (a)}z
w1:=eiArg(a)z
2)放大倍数变换(magnification)
w
2
=
∣
A
∣
w
1
w2 = |A|w1
w2=∣A∣w1
3) 一个平移变换
w
=
w
3
=
w
2
+
B
w = w_3 = w_2 + B
w=w3=w2+B
2.2 逆变换
z
=
φ
−
1
(
w
)
:
=
1
A
(
w
−
B
)
z = φ^{-1}(w) := \frac{1}{A}(w - B)
z=φ−1(w):=A1(w−B)
显然也是一个线性变换。
通过上述分解,原来的变换就可以用相应的矩阵表示。
线性变换中的每一个都是复平面的一对一映射自身。直线和圆的变换分别是直线和圆。并且保证长度不变。
三、反演变换
现在我们考虑由下式定义的反转
w
:
=
1
z
w :=\frac{1}{z}
w:=z1
.
很容易看出,反转是扩展的一对一映射,复平面
C
ˉ
\mathbb{\bar{C}}
Cˉ 到自身上(0 → ∞,反之亦然 ∞ → 0。)
3.1 过原点直线反演
我们将证明一条线的图像要么是一条线,要么是一个圆。
事实上,首先让
l
l
l 通过原点。点
ρ
e
i
θ
ρe^{iθ}
ρeiθ 的图像为
1
ρ
e
−
i
θ
\frac{1}{ρ}e^{-iθ}
ρ1e−iθ 。让 ρ 从负无穷趋向正无穷,我们看到该图像是另一条穿过原点且具有一定倾斜角的线-θ.
3.2 任意直线的反演
现在让 L 由以下方程给出
L
:
A
x
+
B
y
=
C
,
L : Ax + By = C,
L:Ax+By=C,
此时
C
≠
0
,
且
∣
A
∣
+
∣
B
∣
>
0
C\neq 0, 且 |A| + |B| > 0
C=0,且∣A∣+∣B∣>0. (3)
将
w
:
=
1
z
w :=\frac{1}{z}
w:=z1变换一个格式
z
:
=
1
w
z :=\frac{1}{w}
z:=w1,此时,z是直线上点,w是变换后的点。
设:
w
:
=
u
+
i
v
w :=u+iv
w:=u+iv那么:
z
=
w
ˉ
∣
w
∣
2
=
u
−
i
v
u
2
+
v
2
z =\frac{\bar{w}}{|w|^2}=\frac{u − iv}{u^2 + v^2}
z=∣w∣2wˉ=u2+v2u−iv
将z的实部虚部分别引入:
x
=
u
u
2
+
v
2
,
y
=
−
v
u
2
+
v
2
x =\frac{u}{u^2 + v^2}, y =\frac{−v}{u^2 + v^2}
x=u2+v2u,y=u2+v2−v
由于z在直线L之上:
A
u
u
2
+
v
2
+
B
−
v
u
2
+
v
2
=
C
A\frac{u}{u^2 + v^2}+B\frac{−v}{u^2 + v^2}=C
Au2+v2u+Bu2+v2−v=C
化简之后:
u
2
+
v
2
−
A
C
u
+
B
C
v
=
0
u^2+v^2-\frac{A}{C}u+\frac{B}{C}v=0
u2+v2−CAu+CBv=0
显然,w=u+iv自身构成一个圆周。即,不过原点的直线,通过反演变换映射成圆周。
四、莫比乌斯变换
4.1 定义
在复平面上,设定下列变换:
w
=
f
(
z
)
=
a
z
+
b
c
z
+
d
;
,
∣
a
∣
+
∣
c
∣
>
0
,
a
d
−
b
c
≠
0
w = f(z) = \frac{az + b}{cz + d};, |a| + |c| > 0, ad − bc \neq0
w=f(z)=cz+daz+b;,∣a∣+∣c∣>0,ad−bc=0
这个变换称为,莫比乌斯变换。
讨论:
- 如果 c = 0,则莫比乌斯变换是线性的。
- 如果 c ≠ 0 , a = 0 c\neq 0, a = 0 c=0,a=0 那么,变换是一种反演。
- 考虑
a
c
≠
0
ac \neq 0
ac=0 的情况。那么 w 可以是:
写成
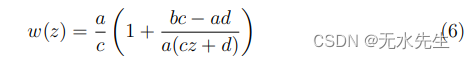
事实上,这是线性变换的分解和反函数。我们还注意到:
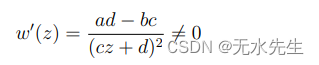
因此,w 在每个点 z ≠ − d / c z \neq -d/c z=−d/c处都是共形的。
4.2 共形性解释
定义(共形映射):若两区域 D 1 D_1 D1和 D 2 D_2 D2 之间的映射,是解析同胚的,则称 是共形映射, D 1 D_1 D1和 D 2 D_2 D2共形等价.
同胚映射是拓扑学中的概念,指两个拓扑空间之间存在一个双射,使得该双射和其逆映射都是连续映射的映射。
共形变换,拓扑同胚,它们的直观解释是:将图画在柔软可拉升的平面皮革上,皮革可以任意卷曲拉伸,但原图像信息扭曲,但不损失。


4.3 莫比乌斯变换特性
定理1:若
f
(
z
)
f(z)
f(z) 在区域
D
D
D 内解析,则在
f
′
(
z
)
≠
0
f'(z) \neq 0
f′(z)=0 的点处,映射
f
(
z
)
f(z)
f(z) 总有保角性、伸缩率不变性.
1)令 f 为莫比乌斯变换。然后f 可以表示为放大、旋转、平移的组合和反演。
2)f 将扩展的复平面映射到其自身上。
3)f 将 Circled 和 Lines 类映射到其自身。
4)f 除其极点外,在每一点都是共形的。
特点:
1.保角性
2.保域性,保圆性,保形性,保对称点性
五、莫比乌斯变换保圆性
1,分式线性函数。分式线性函数也称为分式线性变换,或者 Moibus 变换。它的一般形式为
w = a z + b c z + d , a d − b c ≠ 0 w=\frac{az+b}{cz+d},\qquad ad-bc\ne 0 w=cz+daz+b,ad−bc=0
若
a
d
−
b
c
=
0
ad-bc=0
ad−bc=0 ,则分式线性函数为常数。因为
w
=
a
z
+
b
c
z
+
d
=
a
z
c
z
+
d
+
b
c
z
+
d
=
1
c
⋅
a
(
c
z
+
d
)
c
d
+
d
−
1
c
⋅
a
d
c
z
+
d
+
b
c
z
+
d
=
a
c
−
a
d
−
b
c
c
(
c
z
+
d
)
=
a
c
\begin{align*}w&=\frac{az+b}{cz+d}=\frac{az}{cz+d}+\frac{b}{cz+d}\\ &=\frac{1}{c}\cdot\frac{a(cz+d)}{cd+d}-\frac{1}{c}\cdot\frac{ad}{cz+d}+\frac{b}{cz+d}\\ &=\frac{a}{c}-\frac{ad-bc}{c(cz+d)}=\frac{a}{c}\end{align*}
w=cz+daz+b=cz+daz+cz+db=c1⋅cd+da(cz+d)−c1⋅cz+dad+cz+db=ca−c(cz+d)ad−bc=ca
分式线性函数比较重要,是因为(1)它是单位圆上的全纯自同构群;(2)它是平面上的全纯自同构群;(3)它是扩充复平面上的亚纯自同构群。
这里,直线看成是半径为无穷大的圆。
2,分式线性变换的逆变换(分式线性函数的反函数):
z
=
−
d
w
+
b
c
w
+
a
\displaystyle z=\frac{-dw+b}{cw+a}
z=cw+a−dw+b
3,在扩充复平面上,分式线性函数将
(1)点
z
=
−
d
c
z=-\frac{d}{c}
z=−cd 变成
w
=
∞
w=\infty
w=∞;
(2)
c
=
0
c=0
c=0 时,
z
=
∞
z=\infty
z=∞ 变成
w
=
∞
w=\infty
w=∞;
(3)
c
≠
0
c\ne 0
c=0 时,
z
=
∞
z=\infty
z=∞ 变成
w
=
a
c
w=\frac{a}{c}
w=ca。
4,分式线性变换的分解:分式线性变换可以分解成更简单的一些保形变换的复合。
w
=
a
z
+
b
c
z
+
d
=
a
c
−
a
d
−
b
c
c
(
c
z
+
d
)
,
c
≠
0
w=\frac{az+b}{cz+d}=\frac{a}{c}-\frac{ad-bc}{c(cz+d)},\qquad c\ne 0
w=cz+daz+b=ca−c(cz+d)ad−bc,c=0
w
=
a
z
+
b
c
z
+
d
=
a
d
z
−
b
d
)
=
r
e
i
θ
z
+
b
d
,
c
=
0
w=\frac{az+b}{cz+d}=\frac{a}{d}z-\frac{b}{d)}=re^{i\theta}z+\frac{b}{d},\qquad c=0
w=cz+daz+b=daz−d)b=reiθz+db,c=0
从这里可以看出,分式线性变换可以是下列几种变换的复合:
(1)
w
=
z
+
a
w=z+a
w=z+a,平移变换;
(2)
w
=
e
i
θ
z
w=e^{i\theta}z
w=eiθz,这是旋转变换,其中
θ
\theta
θ 是实数;
(3)
w
=
r
z
w=rz
w=rz,这是相似变换(拉伸),这里 r 是正实数;
(4)
w
=
1
z
w=\frac{1}{z}
w=z1,这称为反演变换。
关于分式线性变换,我们首先有如下的保圆性:
5,定理(分式线性变换的保圆性):在扩充复平面上,分式线性函数将圆变成圆。
证明:(1) w = z + a w=z+a w=z+a,平移变换,将圆变成圆;
(2) w = e i θ z w=e^{i\theta}z w=eiθz,旋转变换,将圆变成圆;
(3) w = r z w=rz w=rz,这是相似变换(拉伸)。只改变圆的大小,不改变形状,还是将圆变成圆;
(4) w = 1 z w=\frac{1}{z} w=z1,反演变换,也将圆变成圆,我们证明如下:
我们知道圆的一般方程为
a
(
x
2
+
y
2
)
+
b
x
+
c
y
+
d
=
0
a(x^2+y^2)+bx+cy+d=0
a(x2+y2)+bx+cy+d=0。若
a
=
0
a=0
a=0
,则圆的方程变成直线,而直线是半径为无穷大的圆。
若 a ≠ 0 a\ne 0 a=0,那么 x 2 + y 2 = z ⋅ z ˉ , x = z + z ˉ 2 , y = z − z ˉ 2 i x^2+y^2=z\cdot \bar{z},\quad x=\frac{z+\bar{z}}{2},\quad y=\frac{z-\bar{z}}{2i} x2+y2=z⋅zˉ,x=2z+zˉ,y=2iz−zˉ
所以圆的方程变为
a z z ˉ + b 2 ( z + z ˉ ) + c 2 i ( a − z ˉ ) + d = 0 a z z ˉ + ( b 2 + c 2 i ) z ( z + z ˉ ) + ( b 2 − c 2 i ) z ˉ + d = 0 a z z ˉ + ( b 2 − c 2 i ) z + ( b 2 + c 2 i ) z ˉ + d = 0 a z z ˉ + β ˉ z + β z ˉ + d = 0 \begin{align*}& az\bar{z}+\frac{b}{2}(z+\bar{z})+\frac{c}{2i}(a-\bar{z})+d=0\\ &az\bar{z}+\left(\frac{b}{2}+\frac{c}{2i}\right)z(z+\bar{z})+\left(\frac{b}{2}-\frac{c}{2i}\right)\bar{z}+d=0\\ &az\bar{z}+\left(\frac{b}{2}-\frac{c}{2}i\right)z+\left(\frac{b}{2}+\frac{c}{2}i\right)\bar{z}+d=0\\ &az\bar{z}+\bar{\beta}z+\beta\bar{z}+d=0\end{align*} azzˉ+2b(z+zˉ)+2ic(a−zˉ)+d=0azzˉ+(2b+2ic)z(z+zˉ)+(2b−2ic)zˉ+d=0azzˉ+(2b−2ci)z+(2b+2ci)zˉ+d=0azzˉ+βˉz+βzˉ+d=0
这就是圆的一般方程的复数表示。这里 β = ( b 2 + c 2 i ) \beta=\left(\frac{b}{2}+\frac{c}{2}i\right) β=(2b+2ci)。
我们将反演变换
w
=
1
z
w=\frac{1}{z}
w=z1
代入上式,得到
a
1
w
⋅
1
w
ˉ
+
β
ˉ
1
w
+
β
1
z
ˉ
+
d
=
0
(
同乘以
w
w
ˉ
)
a
+
β
ˉ
⋅
w
ˉ
+
β
w
+
d
w
w
ˉ
=
0
d
w
w
ˉ
+
β
w
+
β
ˉ
⋅
w
ˉ
+
a
=
0
\begin{align*}&a\frac{1}{w}\cdot\frac{1}{\bar{w}}+\bar{\beta}\frac{1}{w}+\beta\frac{1}{\bar{z}}+d=0\\ (\text{同乘以} w\bar{w})\quad& a+\bar{\beta}\cdot \bar{w}+\beta w+dw\bar{w}=0\\ &dw\bar{w}+\beta w+\bar{\beta}\cdot \bar{w}+a=0\end{align*}
(同乘以wwˉ)aw1⋅wˉ1+βˉw1+βzˉ1+d=0a+βˉ⋅wˉ+βw+dwwˉ=0dwwˉ+βw+βˉ⋅wˉ+a=0
这仍然是一个圆的方程。所以反演变换将圆变成圆。
综合以上四种情形,我们知道,分式线性变换将圆变成圆。因为分式线性变换是由上面四种变换复合而成的。这就证明了分式线性变换的保圆性。
六、关于群
群是一个代数模式,将一种变换
群的定义
如果一个非空集合 G 上定义了一个二元运算
,满足如下性质:
(1)封闭性,即对于
∀
a
,
b
∈
G
\forall a,b \in G
∀a,b∈G ,有
a
⋅
b
∈
G
a \cdot b \in G
a⋅b∈G ;
(2)结合律,即对于
∀
a
,
b
,
c
∈
G
\forall a,b,c \in G
∀a,b,c∈G,有
(
a
⋅
b
)
⋅
c
=
a
⋅
(
b
⋅
c
)
(a \cdot b) \cdot c = a \cdot (b \cdot c)
(a⋅b)⋅c=a⋅(b⋅c) ;
(3)存在
e
∈
G
e \in G
e∈G ,使得
∀
c
∈
G
\forall c \in G
∀c∈G有
e
⋅
c
=
c
⋅
e
=
c
e \cdot c = c \cdot e=c
e⋅c=c⋅e=c
(4)对于
∀
a
∈
G
\forall a \in G
∀a∈G ,存在
∀
b
∈
G
\forall b \in G
∀b∈G ,使得
(
a
⋅
b
)
=
(
b
⋅
a
)
=
e
(a \cdot b)= (b \cdot a)=e
(a⋅b)=(b⋅a)=e
,
则称 G 关于运算
⋅
\cdot
⋅ 构成一个群(group),记为
(
G
,
⋅
)
(G,\cdot)
(G,⋅)
七、莫比乌斯变换群
7.1 结合性证明
(更新中…)