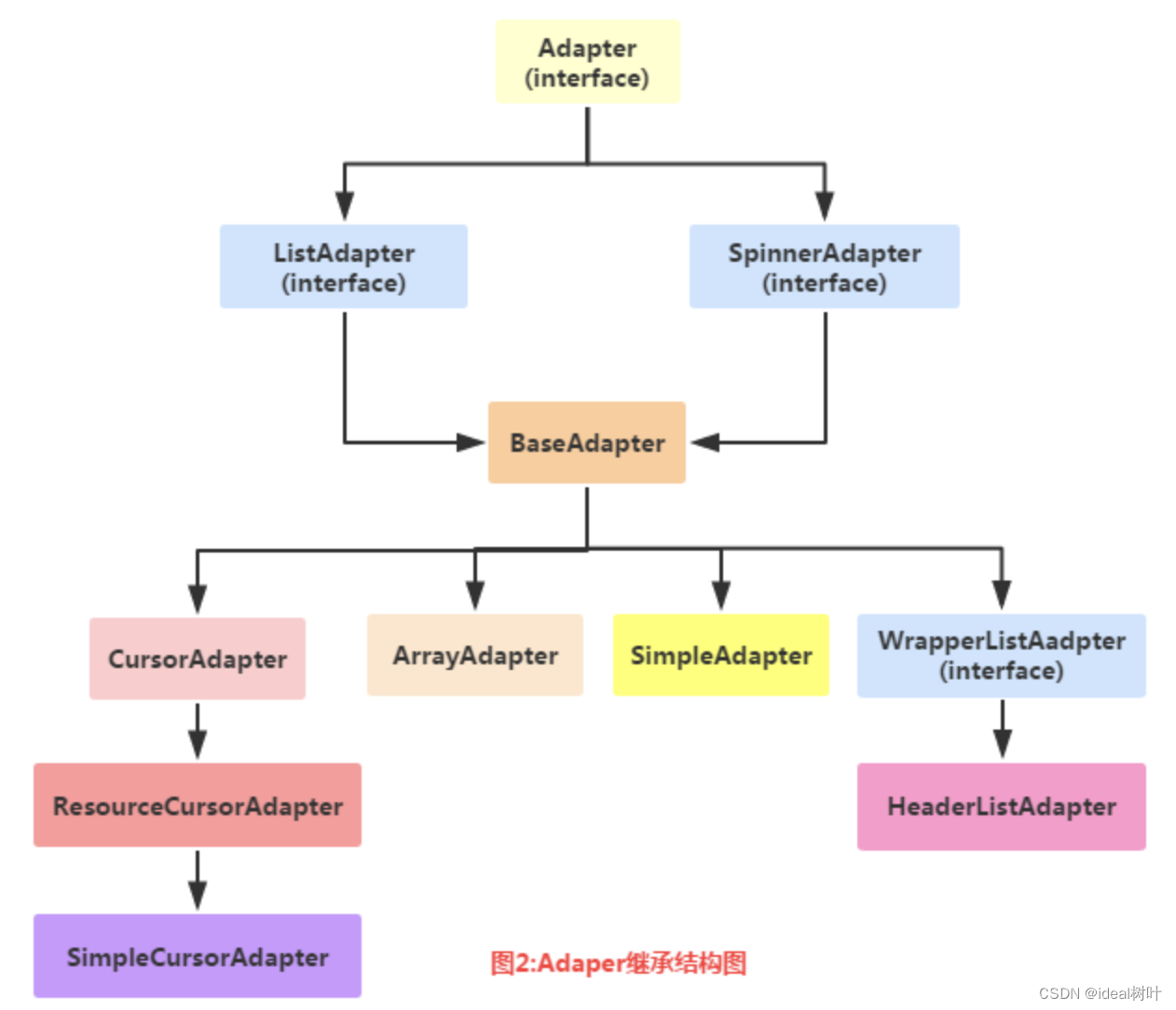
第3讲：基于优化的IMU与视觉信息融合之最小二乘详解

1 最小二乘问题求解

1.1 基础概念

  最小二乘法建模常见于线性（非线性）方程问题中$f_i(x):{\mathbb{R}}^n\to \mathbb{R},i=1,2,\cdots ,m$ 为n元函数(m×n矩阵)，且有如下方程组：
$$b_i=f_i(x),i=1,2,\cdots ,m,$$
  其中 $b_i\in R$ 是已知的实数．方程组的求解在实际中应用广泛，但这个问题并不总是可解的．

  首先，方程组的个数 m 可以超过自变量个数 n(超定方程)，因此方程组的解可能不存在；其次，由于测量误差等因素，方程组的等式关系可能不是精确成立的．为了能在这种实际情况下求解出 x，最小二乘法的思想是极小化误差2范数平方，即
$$\underset{x\in {\mathbb{R}}^n}{\min }\sum _{i=1}^m(b_i-f_i(x){)}^2.$$
  若方程存在解，则求解问题的全局最优解就相当于求出了方程的解；当方程的解不存在时，实际给出了某种程度上误差最小的解．

  最小二乘并不一定是合理的，有时候会根据1范数和无穷范数来构建数学模型：

  保证偏差的绝对值之和最小
$$\underset{x\in {\mathbb{R}}^n}{\min }\sum _{i=1}^m|b_i-f_i(x)|;$$
  保证最大偏差最小化
$$\begin{array}{rlr}& \underset{x\in {\mathbb{R}}^n}{\min }& \underset{i}{\max }|b_i-f_i(x)|.\\ & & \end{array}$$
  注意，如果噪声服从高斯分布，那么最小二乘问题的解对应于原问题的最大似然解。

1.2 总结

残差函数:$f_i$（相当于上面的$f_i-b$），且$m_{观测维度}>n_{变量维度}$，比如测量值与观测值之间的差（因为欠定方程有无穷解，必须正定或超定）

损失函数：$F(x)$，误差函数的平方和，这是一个二次函数，就像$x^2$，存在最小值！

  找到一个n维的变量${\mathbf{x}}^{\ast }\in {\mathbb{R}}^n$（就是要调的参数），使得损失函数$F(x)$取局部最小值
$$F(\mathbf{x})=\frac{1}{2}\sum _{i=1}^m{\left(f_i(\mathbf{x})\right)}^2$$

局部最小值：$\Vert \mathrm{x}-{\mathrm{x}}^{\ast }\Vert <\delta$满足$\begin{array}{r}F\left({\mathbf{x}}^{\ast }\right)\le F(\mathbf{x})\end{array}$，变化微小量函数值下降！

  对损失函数进行二阶泰勒展开，一般忽略高阶项，可以把损失函数看作二次函数。然后，假设我们在${\mathbf{x}}_s$取得局部最小值，那么在点${\mathbf{x}}_s$处的导数为0，即雅可比J为0。
$$F(\mathbf{x}+\Delta \mathbf{x})=F(\mathbf{x})+\mathbf{J}\Delta \mathbf{x}+\frac{1}{2}\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}+O\left(\Vert \Delta \mathbf{x}{\Vert }^3\right)$$

Hessian矩阵在上面条件下，有什么性质？

$$F(\mathbf{x}+\Delta \mathbf{x})=F(\mathbf{x})+\frac{1}{2}\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}$$

1 如果H是正定矩阵，即它的特征值都大于0，则在${\mathbf{x}}_s$处有$F(x)$为局部最小值！（正定二次型$\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}$大于0，所以$F(x_s)-F(\mathbf{x})=F(\mathbf{x}+\Delta \mathbf{x})-F(\mathbf{x})=\frac{1}{2}\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}>0$）

2 如果H是负 定矩阵，即它的特征值都小于0， 则在${\mathbf{x}}_s$处有$F(x)$为局部最大值！

3 如果是不定矩阵，即它的特征值大于0也有小于0，那么在${\mathbf{x}}_s$处为鞍点。

可以从高数的角度来看，对于一个函数，一阶导数为0，二阶导数大于0，说明这个函数是一个凹函数，呈现一个U形，我们得到的极值是最小值；同理一阶导数为0，二阶导数小于0，是一个凸函数，取到极大值；一阶导数为0，二阶导数也为0，说明是一个驻点（鞍点），无法判断。

1.1 基础：最速下降法，牛顿法, 阻尼法

1.1.1 迭代法

  找一个下降方向使损失函数随 x 的迭代逐渐减小，直到 x 收敛到 ${\mathbf{x}}^{\ast }$.

第一步：找下降方向的单位向量d

第二步：确定下降步长$\alpha$

  假设$\alpha$足够小，可以对损失函数$F(x)$进行一阶泰勒展开：
$$F(\mathbf{x}+\alpha \mathbf{d})\approx F(\mathbf{x})+\alpha \mathbf{Jd}$$
  很明显，只要满足下式，即下降方向，就能找到局部最小值：
$$\mathrm{Jd}<0$$

1.1.2 最速下降法（梯度下降）

  最速下降法: 适用于迭代的开始阶段

  从下降方向的条件可知：$\mathbf{Jd}=\Vert \mathbf{J}\Vert \cos \theta$，其中$\theta$表示下降方向与梯度方向的夹角（说白了就是方向导数）。当$\theta =\pi$，有
$$\mathbf{d}=\frac{-{\mathbf{J}}^{\top }}{\Vert \mathbf{J}\Vert }$$
  说明，下降方向的单位向量d就是梯度的负方向，此时下降最快！注意这里没有严格的给出$\Delta \mathbf{x}=\alpha \mathbf{Jd}$，因为方向确定，步长$\alpha$是自己设置的！

  后序的方法一般都会用到二阶导数，所以都会给出相应的$\Delta \mathbf{x}$。

1.1.3 牛顿法

  牛顿法：适用于最优值附近

  在局部最优点${\mathbf{x}}^{\ast }$附近，如果$x+\Delta \mathbf{x}$是最优解，则**损失函数$F(x)$**对$\Delta \mathbf{x}$的导数等于 0，即这一点处变化率为0
$$\frac{\partial }{\partial \Delta \mathbf{x}}\left(F(\mathbf{x})+\mathbf{J}\Delta \mathbf{x}+\frac{1}{2}\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}\right)={\mathbf{J}}^{\top }+\mathbf{H}\Delta \mathbf{x}=0$$
  得到$\Delta \mathbf{x}=-{\mathbf{H}}^{-1}{\mathbf{J}}^{\top }$

1.1.4 阻尼法

  将损失函数的二阶泰勒展开记作
$$F(\mathbf{x}+\Delta \mathbf{x})\approx L(\Delta \mathbf{x})\equiv F(\mathbf{x})+\mathbf{J}\Delta \mathbf{x}+\frac{1}{2}\Delta {\mathbf{x}}^{\top }\mathbf{H}\Delta \mathbf{x}$$
  在原二阶展开后加一个阻尼项，然后求最小化
$$\Delta \mathbf{x}\equiv \arg \underset{\Delta \mathbf{x}}{\min }\left\{L(\Delta \mathbf{x})+\frac{1}{2}\mu \Delta {\mathbf{x}}^{\top }\Delta \mathbf{x}\right\}$$
  µ ≥ 0 为阻尼因子，$\frac{1}{2}\mu \Delta {\mathbf{x}}^{\top }\Delta \mathbf{x}=\frac{1}{2}\mu \Vert \Delta \mathbf{x}{\Vert }^2$是惩罚项。对新的损失函数求一阶导（和牛顿法同理），让其为0，求出变化量：
$$\begin{array}{rl}{\mathbf{L}}^{\prime }(\Delta \mathbf{x})+\mu \Delta \mathbf{x}& =0\\ \Rightarrow (\mathbf{H}+\mu \mathbf{I})\Delta \mathbf{x}& =-{\mathbf{J}}^{\top }\end{array}$$

1.2 进阶：高斯牛顿法，LM 算法的具体实现

1.2.1 非线性最小二乘

① 残差f对优化变量参数x的导数

  为了公式约简，可将残差组合成向量的形式
$$\mathbf{f}(\mathbf{x})=\left[\begin{array}{c}{f}_1(\mathbf{x})\\ ...\\ f_m(\mathbf{x})\end{array}\right]$$
  利用下式就可以得到损失函数F(x)
$${\mathbf{f}}^{\top }(\mathbf{x})\mathbf{f}(\mathbf{x})=\sum _{i=1}^m{\left(f_i(\mathbf{x})\right)}^2$$
  令残差i对优化变量参数x的导数记为（实际上参数x应该有多个，所以实际是一个行向量）：
$${\mathbf{J}}_i(\mathbf{x})=\frac{\partial f_i(\mathbf{x})}{\partial \mathbf{x}}$$
  残差对优化变量的雅可比为（实际上是一个矩阵）：
$$\frac{\partial \mathbf{f}(\mathbf{x})}{\partial \mathbf{x}}=\mathbf{J}=\left[\begin{array}{c}{\mathbf{J}}_1(\mathbf{x})\\ ...\\ {\mathbf{J}}_m(\mathbf{x})\end{array}\right]$$

② 残差f的泰勒展开

  残差函数 f(x) 为非线性函数，对其一阶泰勒近似有
$$\mathbf{f}(\mathbf{x}+\Delta \mathbf{x})\approx \ell (\Delta \mathbf{x})\equiv \mathbf{f}(\mathbf{x})+\mathbf{J}\Delta \mathbf{x}$$
  代入损失函数$F(x)$
$$\begin{array}{rl}F(\mathbf{x}+\Delta \mathbf{x})\approx L(\Delta \mathbf{x})& \equiv \frac{1}{2}\mathbf{\ell }(\Delta \mathbf{x}{)}^{\top }\mathbf{\ell }(\Delta \mathbf{x})\\ & =\frac{1}{2}{\mathbf{f}}^{\top }\mathbf{f}+\Delta {\mathbf{x}}^{\top }{\mathbf{J}}^{\top }\mathbf{f}+\frac{1}{2}\Delta {\mathbf{x}}^{\top }{\mathbf{J}}^{\top }\mathbf{J}\Delta \mathbf{x}\\ & =F(\mathbf{x})+\Delta {\mathbf{x}}^{\top }{\mathbf{J}}^{\top }\mathbf{f}+\frac{1}{2}\Delta {\mathbf{x}}^{\top }{\mathbf{J}}^{\top }\mathbf{J}\Delta \mathbf{x}\end{array}$$

  这样损失函数就近似成了一个二次函数，并且如果雅克比**J**是满秩的，则${\mathbf{J}}^{\top }\mathbf{J}$正定，损失函数有最小值。

为什么这么说？

可以看出$F^{\prime }(\mathbf{x})=({\mathbf{J}}^{\top }\mathbf{f}{)}^{\top },\text{ 以及 }{F}^{\prime \prime }(\mathbf{x})\approx {\mathbf{J}}^{\top }\mathbf{J}$，那么我们就可以用残差f的雅可比来近似损失函数的雅可比与海塞矩阵！既然上面分析过了损失函数在海塞矩阵正定处有最小值，那么这里也是同样的道理！

但是很多时候J都不是满秩的，所以大部分情况都是半正定性！${\mathbf{J}}^{\top }\mathbf{J}$是奇异矩阵（不可逆）或病态。当雅可比接${\mathbf{J}}^{\top }\mathbf{J}$近于0时，无法判断是否存在极小值。其几何含义是存在一个方向（即特征向量），在这个方向上的变化不影响目标函数的值。这意味着在这些方向上，我们可以随意调整变量的值而不会改变目标函数的值，因此最小二乘问题就不再有唯一的解，而有无限多个解。-------存在0空间，0空间维度越大，越不正定！海塞矩阵越病态！

1.2.2 高斯牛顿Gauss-Newton

  对上面的损失函数对$\Delta \mathbf{x}$求一阶导数，令其为0
$$\left({\mathbf{J}}^{\top }\mathbf{J}\right)\Delta {\mathbf{x}}_{\mathrm{gn}}=-{\mathbf{J}}^{\top }\mathbf{f}$$

1.2.3 LM

​ 对高斯牛顿法进行了改进，求解过程中引入了阻尼因子
$$\left({\mathbf{J}}^{\top }\mathbf{J}+\mu \mathbf{I}\right)\Delta {\mathbf{x}}_{\mathrm{lm}}=-{\mathbf{J}}^{\top }\mathbf{f}\mathrm{with}\mu \ge 0$$

关键：阻尼因子有什么作用，怎么设定？

① 阻尼因子的作用

Test CurveFitting start...	
// 其实可以看出来，当μ占比比较大，下降就快;反之，下降就小一点
// 迭代次数		残差^2和		μ			J^T*J对角线均值					最大值
iter: 0 , chi= 36048.3 , Lambda= 0.001 , mean{ J^T*J(i,i) }50.7794		max = 100
iter: 1 , chi= 30015.5 , Lambda= 699.051 , mean{ J^T*J(i,i) }463.093	max = 770
iter: 2 , chi= 13421.2 , Lambda= 1864.14 , mean{ J^T*J(i,i) }5179.29	max = 7447
iter: 3 , chi= 7273.96 , Lambda= 1242.76 , mean{ J^T*J(i,i) }61953.9	max = 43820
iter: 4 , chi= 269.255 , Lambda= 414.252 , mean{ J^T*J(i,i) }34115.8	max = 39009
iter: 5 , chi= 105.473 , Lambda= 138.084 , mean{ J^T*J(i,i) }30504.4	max = 38807
iter: 6 , chi= 100.845 , Lambda= 46.028 , mean{ J^T*J(i,i) }30405.1		...
iter: 7 , chi= 95.9439 , Lambda= 15.3427 , mean{ J^T*J(i,i) }30397
iter: 8 , chi= 92.3017 , Lambda= 5.11423 , mean{ J^T*J(i,i) }30386.6
iter: 9 , chi= 91.442 , Lambda= 1.70474 , mean{ J^T*J(i,i) }30379.6
iter: 10 , chi= 91.3963 , Lambda= 0.568247 , mean{ J^T*J(i,i) }30377.7
iter: 11 , chi= 91.3959 , Lambda= 0.378832 , mean{ J^T*J(i,i) }30377.5

② 阻尼因子的初始值选取

​  取对角线元素最大值与一个常数的乘积，其中$\tau \sim [10^{-8},1]$.
$${\mu }_0=\tau \cdot \max \left\{{\left({\mathbf{J}}^{\top }\mathbf{J}\right)}_{ii}\right\}$$

double maxDiagonal = 0;
ulong size = Hessian_.cols();

// 通过对 Hessian 矩阵的对角元素取绝对值并找到最大值，计算了用于更新 Lambda 的参数 currentLambda_
// 上面给出iter = 0，对角线max = 100，那么1e-5*100刚好就是lambda = 0.001---是没问题的
for (ulong i = 0; i < size; ++i) {
    maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal);
}

double tau = 1e-5;
currentLambda_ = tau * maxDiagonal;

③ 阻尼因子的更新策略

    double scale = 0;
    // 分母 = 近似模型下降的值
    scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
    scale += 1e-3;    // make sure it's non-zero :)

    // recompute residuals after update state
    // 统计所有的残差
    double tempChi = 0.0;
    for (auto edge: edges_) {
        edge.second->ComputeResidual();
        tempChi += edge.second->Chi2();
    }
    // 实际函数下降的值 = currentChi_ - tempChi
    // ρ
    double rho = (currentChi_ - tempChi) / scale;

  $\rho$的分子是实际函数下降的值，分母是近似模型下降的值。如果$\rho$接近于1，则近似是好的。如果$\rho$太小，说明实际减小的值远少于近似减小的值，则认为近似比较差，需要缩小近似范围。反之，如果$\rho$比较大，则说明实际下降的比预计的更大，我们可以放大近似范围。
$$\rho =\frac{f(\mathbf{x}+\Delta \mathbf{x})-f(\mathbf{x})}{\mathbf{J}(\mathbf{x}{)}^{\mathrm{T}}\Delta \mathbf{x}}$$

• g2o, ceres 采用

    // tempChi 是有限值
    if (rho > 0 && isfinite(tempChi))   // last step was good, 误差在下降
    {
        double alpha = 1. - pow((2 * rho - 1), 3);
        alpha = std::min(alpha, 2. / 3.);
        double scaleFactor = (std::max)(1. / 3., alpha);
        currentLambda_ *= scaleFactor;
        ni_ = 2;        // v = 2
        currentChi_ = tempChi;
        return true;
    } else {
        currentLambda_ *= ni_;      // μ = μ * v
        ni_ *= 2;                   // v = 2 * v
        return false;
    }

  大于0说明确实下降了，反之没有下降，这次迭代是有问题的

1.2.4 总结

​  GN和LM与1.1节的方法区别就在于一个用的是残差函数的雅可比，一个用的是损失函数的雅可比！

1.3 终极：鲁棒核函数的实现

  鲁棒核函数直接作用残差$f_k(\mathbf{x})$上，最小二乘函数（损失函数变成了如下形式

$$\underset{\mathbf{x}}{\min }\frac{1}{2}\sum _k\rho \left(\Vert f_k(\mathbf{x}){\Vert }^2\right)$$
​ 将误差的平方项记作$s_k={\Vert f_k(\mathbf{x})\Vert }^2$, 则鲁棒核误差函数进行二阶泰勒展开有

$$\frac{1}{2}\rho \left(s\right)=\frac{1}{2}(const+{\rho }^{\prime }\Delta s+\frac{1}{2}{\rho }^{\prime \prime }{\Delta }^{2}s)$$

1 优化参数变量之变化量$\Delta s_k$

$$\begin{array}{rl}\Delta s_k& ={\Vert f_k(\mathbf{x}+\Delta \mathbf{x})\Vert }^2-{\Vert f_k(\mathbf{x})\Vert }^2\\ & \approx {\Vert f_k+{\mathbf{J}}_k\Delta \mathbf{x}\Vert }^2-{\Vert f_k(\mathbf{x})\Vert }^2\\ & =2f_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}\end{array}$$

2 代入$\Delta s_k$

$$\begin{array}{rl}\frac{1}{2}\rho \left(s\right)& \begin{array}{r}\approx \frac{1}{2}({\rho }^{\prime }[2f_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}]\end{array}\\ & +\frac{1}{2}{\rho }^{\prime \prime }[2f_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}{]}^2+const)\\ & \approx {\rho }^{\prime }{f}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+\frac{1}{2}{\rho }^{\prime }(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+{\rho }^{\prime \prime }(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }{f}_k{f}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+const\\ & ={\rho }^{\prime }{f}_k^{\top }{\mathbf{J}}_k\Delta \mathbf{x}+\frac{1}{2}(\Delta \mathbf{x}{)}^{\top }{\mathbf{J}}_k^{\top }({\rho }^{\prime }I+2{\rho }^{\prime \prime }{f}_k{f}_k^{\top }){\mathbf{J}}_k\Delta \mathbf{x}+const\end{array}$$

3 对$\Delta x$求一阶导数，变化率为0处

$$\begin{array}{r}\sum _k{\mathbf{J}}_k^{\top }({\rho }^{\prime }I+2{\rho }^{\prime \prime }{f}_k{f}_k^{\top }){\mathbf{J}}_k\Delta \mathbf{x}=-\sum _k{\rho }^{\prime }{\mathbf{J}}_k^{\top }{f}_k\\ \sum _k{\mathbf{J}}_k^{\top }W{\mathbf{J}}_k\Delta \mathbf{x}=-\sum _k{\rho }^{\prime }{\mathbf{J}}_k^{\top }{f}_k\end{array}$$

eg：柯西鲁棒核函数，其中 c 为控制参数

$$\rho (s)=c^2\log (1+\frac{s}{c^2})$$

$${\rho }^{\prime }(s)=\frac{1}{1+\frac{s}{c^2}},{\rho }^{\prime \prime }(s)=-\frac{1}{c^2}({\rho }^{\prime }(s){)}^2$$

参数c的设定

1.4 如何构建最小二乘

1 残差函数f

2 残差函数f对优化参数变量x的雅可比j

3 构建损失函数cost function 及参数

4 LM算法求解

2 代码解析

​  这里提供了用eigen写的g2o的优化方法，是很值得去学习的！代码核心就是后端backend文件下的代码。

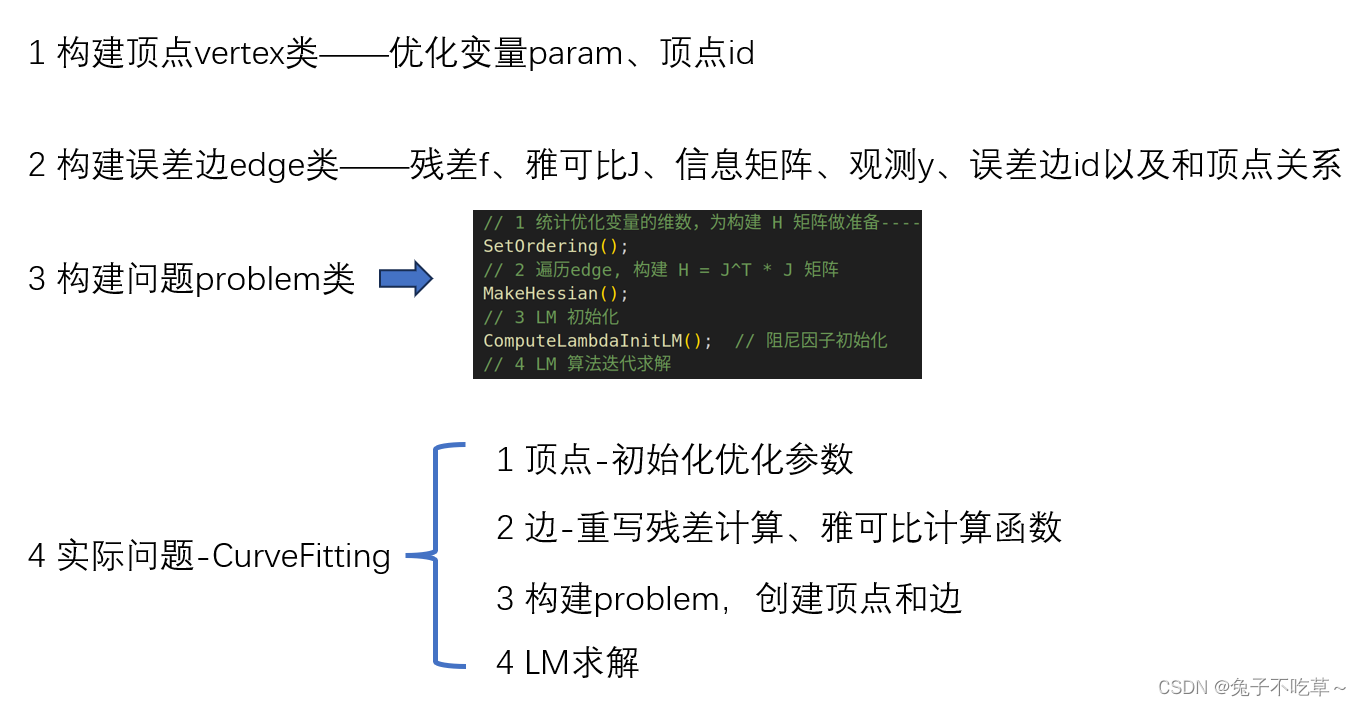
2.1 顶点vertex

​  顶点的实现有几个关键：① 顶点初始化，这个顶点的维度，比如曲线拟合中有三个参数，那么他就是3为变量；② 优化量的更新 x += Δx

① vertex.h

#ifndef MYSLAM_BACKEND_VERTEX_H
#define MYSLAM_BACKEND_VERTEX_H

#include <backend/eigen_types.h>

namespace myslam {
namespace backend {

/**
 * @brief 顶点，对应一个parameter block
 * 变量值以VecX存储，需要在构造时指定维度
 */
class Vertex {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    /**
     * 构造函数 要搞清楚优化变量维度和有多少个优化变量的区别，不能混肴
     * @param num_dimension 顶点自身维度,对于位姿，可以是6为李代数；
     *                      对于曲线拟合，是n个参数组成的向量。
     * 						位姿作为优化变量，有很多个不同的位姿
     						但曲线拟合参数只有一组，所以顶点只有一个
     * @param local_dimension 本地参数化维度，为-1时认为与本身维度一样
     */     // explicit防止隐式转换数据类型
    explicit Vertex(int num_dimension, int local_dimension = -1);

    // virtual用于声明虚函数，派生类可以重写这些函数
    virtual ~Vertex();

    /// 返回变量维度
    int Dimension() const;

    /// 返回变量本地维度
    int LocalDimension() const;

    /// 该顶点的id
    unsigned long Id() const { return id_; }

    /// 返回参数值
    VecX Parameters() const { return parameters_; }

    /// 返回参数值的引用
    VecX &Parameters() { return parameters_; }

    /// 设置参数值
    void SetParameters(const VecX &params) { parameters_ = params; }

    /// 加法，可重定义
    /// 默认是向量加------对于曲线拟合、landmark，参数x = x + Δx
    // 但要是位姿这种优化变量，就不能直接用加法！
    virtual void Plus(const VecX &delta);

    /// 返回顶点的名称，在子类中实现
    virtual std::string TypeInfo() const = 0;

    int OrderingId() const { return ordering_id_; }

    void SetOrderingId(unsigned long id) { ordering_id_ = id; };

    /// 固定该点的估计值
    void SetFixed(bool fixed = true) {
        fixed_ = fixed;
    }

    /// 测试该点是否被固定
    bool IsFixed() const { return fixed_; }

protected:
    VecX parameters_;   // 实际存储的变量值
    int local_dimension_;   // 局部参数化维度
    unsigned long id_;  // 顶点的id，自动生成

    /// ordering id是在problem中排序后的id，用于寻找雅可比对应块
    /// ordering id带有维度信息，例如ordering_id=6则对应Hessian中的第6列
    /// 从零开始
    unsigned long ordering_id_ = 0;

    bool fixed_ = false;    // 是否固定
};

}
}

#endif

② vertex.cc

#include "backend/vertex.h"
#include <iostream>

namespace myslam {
namespace backend {

unsigned long global_vertex_id = 0;	// 全局变量，建立一个顶点，就会++1次

Vertex::Vertex(int num_dimension, int local_dimension) {
    parameters_.resize(num_dimension, 1);
    local_dimension_ = local_dimension > 0 ? local_dimension : num_dimension;
    id_ = global_vertex_id++;

//    std::cout << "Vertex construct num_dimension: " << num_dimension
//              << " local_dimension: " << local_dimension << " id_: " << id_ << std::endl;
}

Vertex::~Vertex() {}

int Vertex::Dimension() const {
    return parameters_.rows();	// 优化变量维度(当前顶点维度)
}

int Vertex::LocalDimension() const {
    return local_dimension_;
}

void Vertex::Plus(const VecX &delta) {
    parameters_ += delta;	// 每次参数的迭代更新
}

}
}

2.2 边edge

​  误差-边要做的事情相对较多，但是计算残差、雅可比这几个重要的基本上在主函数里面实现。

① edge.h

namespace myslam {
namespace backend {

class Vertex;

/**
 * 边负责计算残差，残差是 预测-观测，维度在构造函数中定义
 * 代价函数是 残差*信息*残差，是一个数值，由后端求和后最小化
 */
class Edge {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    /**
     * 构造函数，会自动化配雅可比的空间
     * @param residual_dimension 残差维度
     * @param num_verticies 顶点数量
     * @param verticies_types 顶点类型名称，可以不给，不给的话check中不会检查
     */
    explicit Edge(int residual_dimension, int num_verticies,
                  const std::vector<std::string> &verticies_types = std::vector<std::string>());

    virtual ~Edge();

    /// 返回id
    unsigned long Id() const { return id_; }

    /**
     * 设置一个顶点--在容器的尾部插入一个顶点
     * @param vertex 对应的vertex对象
     */
    bool AddVertex(std::shared_ptr<Vertex> vertex) {
        verticies_.emplace_back(vertex);
        return true;
    }

    /**
     * 设置一些顶点
     * @param vertices 顶点，按引用顺序排列
     * @return
     */
    bool SetVertex(const std::vector<std::shared_ptr<Vertex>> &vertices) {
        verticies_ = vertices;
        return true;
    }

    /// 返回第i个顶点
    std::shared_ptr<Vertex> GetVertex(int i) {
        return verticies_[i];
    }

    /// 返回所有顶点
    std::vector<std::shared_ptr<Vertex>> Verticies() const {
        return verticies_;
    }

    /// 返回关联顶点个数
    size_t NumVertices() const { return verticies_.size(); }

    /// 返回边的类型信息，在子类中实现
    virtual std::string TypeInfo() const = 0;

    /// 计算残差，由子类实现
    virtual void ComputeResidual() = 0;

    /// 计算雅可比，由子类实现
    /// 本后端不支持自动求导，需要实现每个子类的雅可比计算方法
    virtual void ComputeJacobians() = 0;

//    ///计算该edge对Hession矩阵的影响，由子类实现
//    virtual void ComputeHessionFactor() = 0;

    /// 计算平方误差，会乘以信息矩阵
    double Chi2();

    /// 返回残差
    VecX Residual() const { return residual_; }

    /// 返回雅可比
    std::vector<MatXX> Jacobians() const { return jacobians_; }

    /// 设置信息矩阵, information_ = sqrt_Omega = w
    void SetInformation(const MatXX &information) {
        information_ = information;
    }

    /// 返回信息矩阵
    MatXX Information() const {
        return information_;
    }

    /// 设置观测信息
    void SetObservation(const VecX &observation) {
        observation_ = observation;
    }

    /// 返回观测信息
    VecX Observation() const { return observation_; }

    /// 检查边的信息是否全部设置
    bool CheckValid();

    int OrderingId() const { return ordering_id_; }

    void SetOrderingId(int id) { ordering_id_ = id; };

protected:
    unsigned long id_;  // edge id
    int ordering_id_;   //edge id in problem
    std::vector<std::string> verticies_types_;  // 各顶点类型信息，用于debug
    std::vector<std::shared_ptr<Vertex>> verticies_; // 该边对应的顶点
    VecX residual_;                 // 残差
    std::vector<MatXX> jacobians_;  // 雅可比，每个雅可比维度是 residual x vertex[i]
    MatXX information_;             // 信息矩阵
    VecX observation_;              // 观测信息
};

}

② edge.cc

namespace myslam {
namespace backend {

unsigned long global_edge_id = 0;

Edge::Edge(int residual_dimension, int num_verticies,
           const std::vector<std::string> &verticies_types) {
    residual_.resize(residual_dimension, 1);
//    verticies_.resize(num_verticies);      // TODO:: 这里可能会存在问题，比如这里resize了3个空,后续调用edge->addVertex. 使得vertex前面会存在空元素
    if (!verticies_types.empty())
        verticies_types_ = verticies_types;
    jacobians_.resize(num_verticies);
    id_ = global_edge_id++;

    Eigen::MatrixXd information(residual_dimension, residual_dimension);
    information.setIdentity();
    information_ = information;

}

Edge::~Edge() {}
//最小二乘
double Edge::Chi2() {
    // TODO::  we should not Multiply information here, because we have computed Jacobian = sqrt_info * Jacobian
    return residual_.transpose() * information_ * residual_;
//    return residual_.transpose() * residual_;   // 当计算 residual 的时候已经乘以了 sqrt_info, 这里不要再乘
}

bool Edge::CheckValid() {
    if (!verticies_types_.empty()) {
        // check type info
        for (size_t i = 0; i < verticies_.size(); ++i) {
            if (verticies_types_[i] != verticies_[i]->TypeInfo()) {
                cout << "Vertex type does not match, should be " << verticies_types_[i] <<
                     ", but set to " << verticies_[i]->TypeInfo() << endl;
                return false;
            }
        }
    }
    return true;
}
}

2.3 problem

​  对于边和顶点的编写是比较简易的，求解一个问题就是要利用边和顶点去优化。所以这部分是比较复杂的。

① problem.h

/// 整个信息矩阵
    MatXX Hessian_;
    VecX b_;
    VecX delta_x_;

    /// 先验部分信息
    MatXX H_prior_;
    VecX b_prior_;
    MatXX Jt_prior_inv_;
    VecX err_prior_;

    /// SBA的Pose部分-------------SBA（Sparse Bundle Adjustment）
    MatXX H_pp_schur_;
    VecX b_pp_schur_;
    // Heesian 的 Landmark 和 pose 部分
    MatXX H_pp_;
    VecX b_pp_;
    MatXX H_ll_;
    VecX b_ll_;

    /// all vertices----------哈希---------map<int, vertex>
    HashVertex verticies_;

    /// all edges
    HashEdge edges_;

    /// 由vertex id查询edge
    HashVertexIdToEdge vertexToEdge_;

• 优化顺序（Ordering）相关的变量

    /// Ordering related
    ulong ordering_poses_ = 0;
    ulong ordering_landmarks_ = 0;
    ulong ordering_generic_ = 0;
    std::map<unsigned long, std::shared_ptr<Vertex>> idx_pose_vertices_;        // 以ordering排序的pose顶点
    std::map<unsigned long, std::shared_ptr<Vertex>> idx_landmark_vertices_;    // 以ordering排序的landmark顶点

    // verticies need to marg. <Ordering_id_, Vertex>
    HashVertex verticies_marg_;

    bool bDebug = false;
    double t_hessian_cost_ = 0.0;
    double t_PCGsovle_cost_ = 0.0;

② problem.cc

a 添加顶点和边

​  注意顶点的id是自动生成的，还有哈希边向量edges_就是在N次观测中通过AddEdge建立的，后续都会处理edges_

// 新建一个顶点,存储到哈希顶点向量中
bool Problem::AddVertex(std::shared_ptr<Vertex> vertex) {
    // map容器查找元素,如果目标元素不存在，则返回指向容器末尾的迭代器
    if (verticies_.find(vertex->Id()) != verticies_.end()) {
        // LOG(WARNING) << "Vertex " << vertex->Id() << " has been added before";
        return false;
    } else {
        verticies_.insert(pair<unsigned long, shared_ptr<Vertex>>(vertex->Id(), vertex));
    }

    return true;
}


// 新建一个edge,存储到哈希edge向量中
bool Problem::AddEdge(shared_ptr<Edge> edge) {
    if (edges_.find(edge->Id()) == edges_.end()) {
        edges_.insert(pair<ulong, std::shared_ptr<Edge>>(edge->Id(), edge));
    } else {
        // LOG(WARNING) << "Edge " << edge->Id() << " has been added before!";
        return false;
    }
    // 把这条边连接的顶点记录map<顶点id，边>
    for (auto &vertex: edge->Verticies()) {
        vertexToEdge_.insert(pair<ulong, shared_ptr<Edge>>(vertex->Id(), edge));
    }
    return true;
}

b 求解函数Solve

​  false_cnt 是一个整型变量，用于记录在LM算法迭代过程中出现误差没有下降的次数

bool Problem::Solve(int iterations) {


    if (edges_.size() == 0 || verticies_.size() == 0) {
        std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;
        return false;
    }

    TicToc t_solve;
    // 1 统计优化变量的维数，为构建 H 矩阵做准备----比如曲线拟合，一个顶点，优化三个参数，这里就是3维
    SetOrdering();
    // 2 遍历edge, 构建 H = J^T * J 矩阵
    MakeHessian();
    // 3 LM 初始化
    ComputeLambdaInitLM();  // 阻尼因子初始化
    // 4 LM 算法迭代求解
    bool stop = false;
    int iter = 0;
    while (!stop && (iter < iterations)) {
        std::cout << "iter: " << iter << " , chi= " << currentChi_ 
                  << " , Lambda= " << currentLambda_
                  << " , mean{ H(i,i) }" << Hessian_.diagonal().mean()
                  << std::endl;
        bool oneStepSuccess = false;
        int false_cnt = 0;
        while (!oneStepSuccess)  // 不断尝试 Lambda, 直到成功迭代一步
        {
            // setLambda    (JJ+μI)Δx = JF
            AddLambdatoHessianLM();

            // 第四步，解线性方程 H X = B   (JJ+μI)Δx = JF
            SolveLinearSystem();

            // 求出增量后还原海塞矩阵H
            RemoveLambdaHessianLM();   //  (JJ)Δx = JF

            // 优化退出条件1： delta_x_ 很小则退出--------曲线拟合在这里退出了，很难讲误差减小到原来的1e-6
            if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
                stop = true;
                break;
            }

            // 更新状态量 X = X+ delta_x
            UpdateStates();
            // 判断当前步是否可行以及 LM 的 lambda 怎么更新
            oneStepSuccess = IsGoodStepInLM();
            // std::cout << " , Lambda= " << currentLambda_  << std::endl;
            if (oneStepSuccess)     // 当前步可行
            {
                // 在新线性化点 构建 hessian
                MakeHessian();
                // TODO:: 这个判断条件可以丢掉，条件 b_max <= 1e-12 很难达到，这里的阈值条件不应该用绝对值，而是相对值
                //                double b_max = 0.0;
                //                for (int i = 0; i < b_.size(); ++i) {
                //                    b_max = max(fabs(b_(i)), b_max);
                //                }
                //                // 优化退出条件2： 如果残差 b_max 已经很小了，那就退出
                //                stop = (b_max <= 1e-12);
                false_cnt = 0;
            } 
            else    // 当前步不可行
            {
                false_cnt++;        // 记录在LM算法迭代过程中出现误差没有下降的次数
                RollbackStates();   // 误差没下降，回滚
            }
        }
        iter++;

        // 优化退出条件3： currentChi_ 跟第一次的chi2相比，下降了 1e6 倍则退出
        if (sqrt(currentChi_) <= stopThresholdLM_)
            stop = true;
    }
    std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;
    std::cout << "   makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;
    return true;
}

统计优化变量的维度

​  比如曲线拟合只有一个顶点，包括3个优化量；如果是位姿，假设一个位姿用6维李代数表示，那么n个位姿是6n维，海塞矩阵就是6n*6n（只优化位姿）

void Problem::SetOrdering() {

    // 每次重新计数
    ordering_poses_ = 0;
    ordering_generic_ = 0;
    ordering_landmarks_ = 0;

    // Note:: verticies_ 是 map 类型的, 顺序是按照 id 号排序的
    // 统计带估计的所有变量的总维度-----
    for (auto vertex: verticies_) {
        ordering_generic_ += vertex.second->LocalDimension();  // 所有的优化变量总维数
    }
}

MakeHessian构建海塞矩阵

​  构建海塞矩阵要搞清楚，矩阵中每一块对应着什么！J^T * J，对于曲线拟合是非常简单的，只有一个顶点，H也只是3*3.但是要是求解姿态，优化变量就有位姿和路标点两种，会构建一个特别的稀疏矩阵。

void Problem::MakeHessian() {
    TicToc t_h;
    // 直接构造大的 H 矩阵
    ulong size = ordering_generic_;     // 所有的优化变量总维数---曲线拟合就是3---位姿6n+3m
    MatXX H(MatXX::Zero(size, size));
    VecX b(VecX::Zero(size));

    // TODO:: accelate, accelate, accelate
    //#ifdef USE_OPENMP
    //#pragma omp parallel for
    //#endif

    // 遍历每个残差，并计算他们的雅克比，得到最后的 H = J^T * J
    for (auto &edge: edges_) {

        edge.second->ComputeResidual();     // 由子类实现abc(0)*x_*x_ + abc(1)*x_ + abc(2)  - y_
        edge.second->ComputeJacobians();    // jaco_abc << x_ * x_ , x_  , 1 ;   1*3

        auto jacobians = edge.second->Jacobians();  // std::vector<MatXX>
        auto verticies = edge.second->Verticies();  // 返回所有顶点

        // *****************************
        // 这里是一元边，即一条边连接一个顶点，一条误差边对应一个雅可比，所以顶点数==边数
        assert(jacobians.size() == verticies.size());   // 注意这里是一条误差边对应的雅可比，即1*3
        
        for (size_t i = 0; i < verticies.size(); ++i) 
        {
            auto v_i = verticies[i];
            if (v_i->IsFixed()) continue;    // Hessian 里不需要添加它的信息，也就是它的雅克比为 0

            auto jacobian_i = jacobians[i];
            ulong index_i = v_i->OrderingId();  // 用于寻找雅可比对应块
            ulong dim_i = v_i->LocalDimension();

            MatXX JtW = jacobian_i.transpose() * edge.second->Information();
            for (size_t j = i; j < verticies.size(); ++j) {
                auto v_j = verticies[j];

                if (v_j->IsFixed()) continue;

                auto jacobian_j = jacobians[j];
                ulong index_j = v_j->OrderingId();
                ulong dim_j = v_j->LocalDimension();

                assert(v_j->OrderingId() != -1);
                MatXX hessian = JtW * jacobian_j;       // J^T*Info*J
                
                // 所有的信息矩阵叠加起来
                // 使用 noalias() 可以告诉编译器，可以直接在目标矩阵上进行运算，而无需创建中间临时矩阵。
                H.block(index_i, index_j, dim_i, dim_j).noalias() += hessian;
                if (j != i) {
                    // 对称的下三角
                    H.block(index_j, index_i, dim_j, dim_i).noalias() += hessian.transpose();
                }
            }
            b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();
        }

    }
    Hessian_ = H;
    b_ = b;
    t_hessian_cost_ += t_h.toc();

    delta_x_ = VecX::Zero(size);  // initial delta_x = 0_n;

}

计算LM之阻尼因子初始值

// LM
void Problem::ComputeLambdaInitLM() {
    ni_ = 2.;
    currentLambda_ = -1.;
    currentChi_ = 0.0;
    // TODO:: robust cost chi2
    for (auto edge: edges_) {
        currentChi_ += edge.second->Chi2();
    }
    if (err_prior_.rows() > 0)
        currentChi_ += err_prior_.norm();

    // 停止条件 
    stopThresholdLM_ = 1e-6 * currentChi_;          // 迭代条件为 误差下降 1e-6 倍


    // 选取阻尼因子的初始值
    double maxDiagonal = 0;
    ulong size = Hessian_.cols();
    assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");

    // 通过对 Hessian 矩阵的对角元素取绝对值并找到最大值，计算了用于更新 Lambda 的参数 currentLambda_
    for (ulong i = 0; i < size; ++i) {
        maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal);
    }

    double tau = 1e-5;
    currentLambda_ = tau * maxDiagonal;
}

添加阻尼因子$\mu$

void Problem::AddLambdatoHessianLM() {
    ulong size = Hessian_.cols();

    assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");

    for (ulong i = 0; i < size; ++i) {
        Hessian_(i, i) += currentLambda_;   // (JJ+μI)Δx = JF
    }
}

2.4 CurveFitting

​ 这里重写了相应的顶点和边，构建了最小二乘问题，经过迭代得到最优解

#include <iostream>
#include <random>
#include "backend/problem.h"

using namespace myslam::backend;
using namespace std;

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class CurveFittingVertex: public Vertex
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    CurveFittingVertex(): Vertex(3) {}  // abc: 三个参数， Vertex 是 3 维的
    virtual std::string TypeInfo() const { return "abc"; }
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class CurveFittingEdge: public Edge
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    CurveFittingEdge( double x, double y ): Edge(1,1, std::vector<std::string>{"abc"}) {
        x_ = x;
        y_ = y;     // 赋值-真实值
    }
    // 计算曲线模型误差
    virtual void ComputeResidual() override
    {
        Vec3 abc = verticies_[0]->Parameters();  // 估计的参数
        residual_(0) = std::exp( abc(0)*x_*x_ + abc(1)*x_ + abc(2) ) - y_;  // 构建残差
        // residual_(0) = abc(0)*x_*x_ + abc(1)*x_ + abc(2)  - y_;  // 构建残差
    }

    // 计算残差对变量的雅克比
    virtual void ComputeJacobians() override
    {
        Vec3 abc = verticies_[0]->Parameters();
        double exp_y = std::exp( abc(0)*x_*x_ + abc(1)*x_ + abc(2) );

        Eigen::Matrix<double, 1, 3> jaco_abc;  // 误差为1维，状态量 3 个，所以是 1x3 的雅克比矩阵
        jaco_abc << x_ * x_ * exp_y, x_ * exp_y , 1 * exp_y;
        // jaco_abc << x_ * x_ , x_  , 1 ;
        jacobians_[0] = jaco_abc;
    }
    /// 返回边的类型信息
    virtual std::string TypeInfo() const override { return "CurveFittingEdge"; }
public:
    double x_,y_;  // x 值， y 值为 _measurement
};

int main()
{
    double a=1.0, b=2.0, c=1.0;         // 真实参数值
    // double a=10, b=20, c=10;         // 真实参数值
    int N = 100;                          // 数据点
    double w_sigma= 1.;                 // 噪声Sigma值

    std::default_random_engine generator;
    std::normal_distribution<double> noise(0.,w_sigma);

    // 1 构建 problem
    Problem problem(Problem::ProblemType::GENERIC_PROBLEM);

    // 2 构建顶点
    shared_ptr< CurveFittingVertex > vertex(new CurveFittingVertex());

    // 设定待估计参数 a, b, c初始值
    vertex->SetParameters(Eigen::Vector3d (0.,0.,0.));
    // 3 将待估计的参数加入最小二乘问题
    problem.AddVertex(vertex);

    // 4 构造 N 次观测(误差边)
    for (int i = 0; i < N; ++i) {

        double x = i/100.;
        double n = noise(generator);
        // 观测 y
        double y = std::exp( a*x*x + b*x + c ) + n;
        // double y =  a*x*x + b*x + c + n;

        // 每个观测对应的残差函数
        shared_ptr< CurveFittingEdge > edge(new CurveFittingEdge(x,y));
        std::vector<std::shared_ptr<Vertex>> edge_vertex;
        edge_vertex.push_back(vertex);
        edge->SetVertex(edge_vertex);

        // 把这个残差添加到最小二乘问题
        problem.AddEdge(edge);
    }

    std::cout<<"\nTest CurveFitting start..."<<std::endl;
    // 5 使用 LM 求解
    problem.Solve(30);

    std::cout << "-------After optimization, we got these parameters :" << std::endl;
    std::cout << vertex->Parameters().transpose() << std::endl;
    std::cout << "-------ground truth: " << std::endl;
    std::cout << "1.0,  2.0,  1.0" << std::endl;

    // std
    return 0;
}