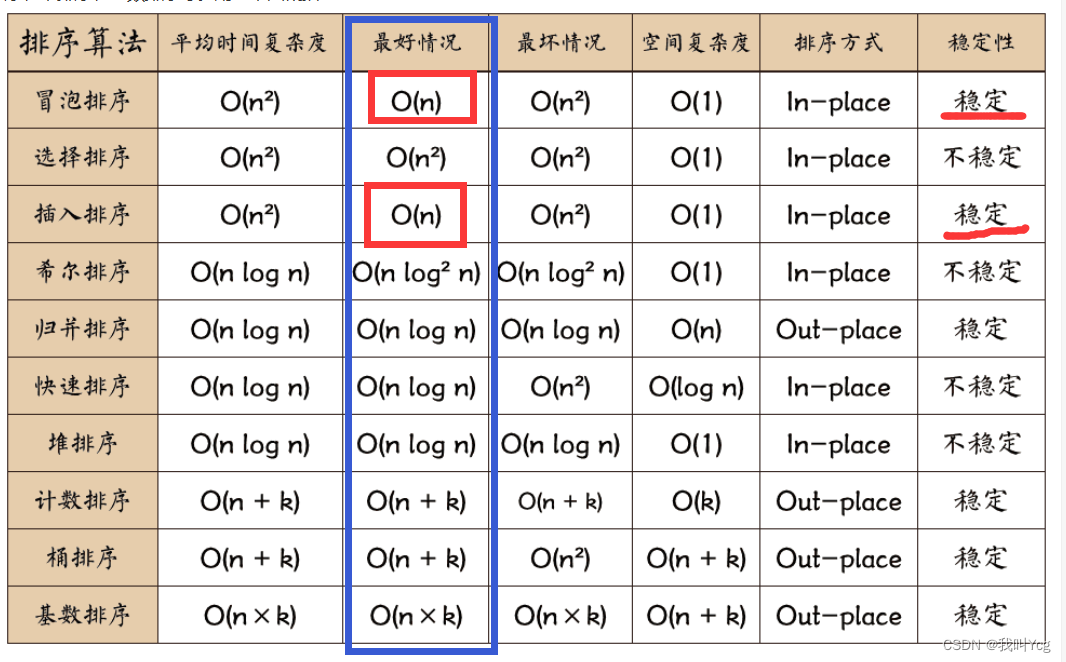
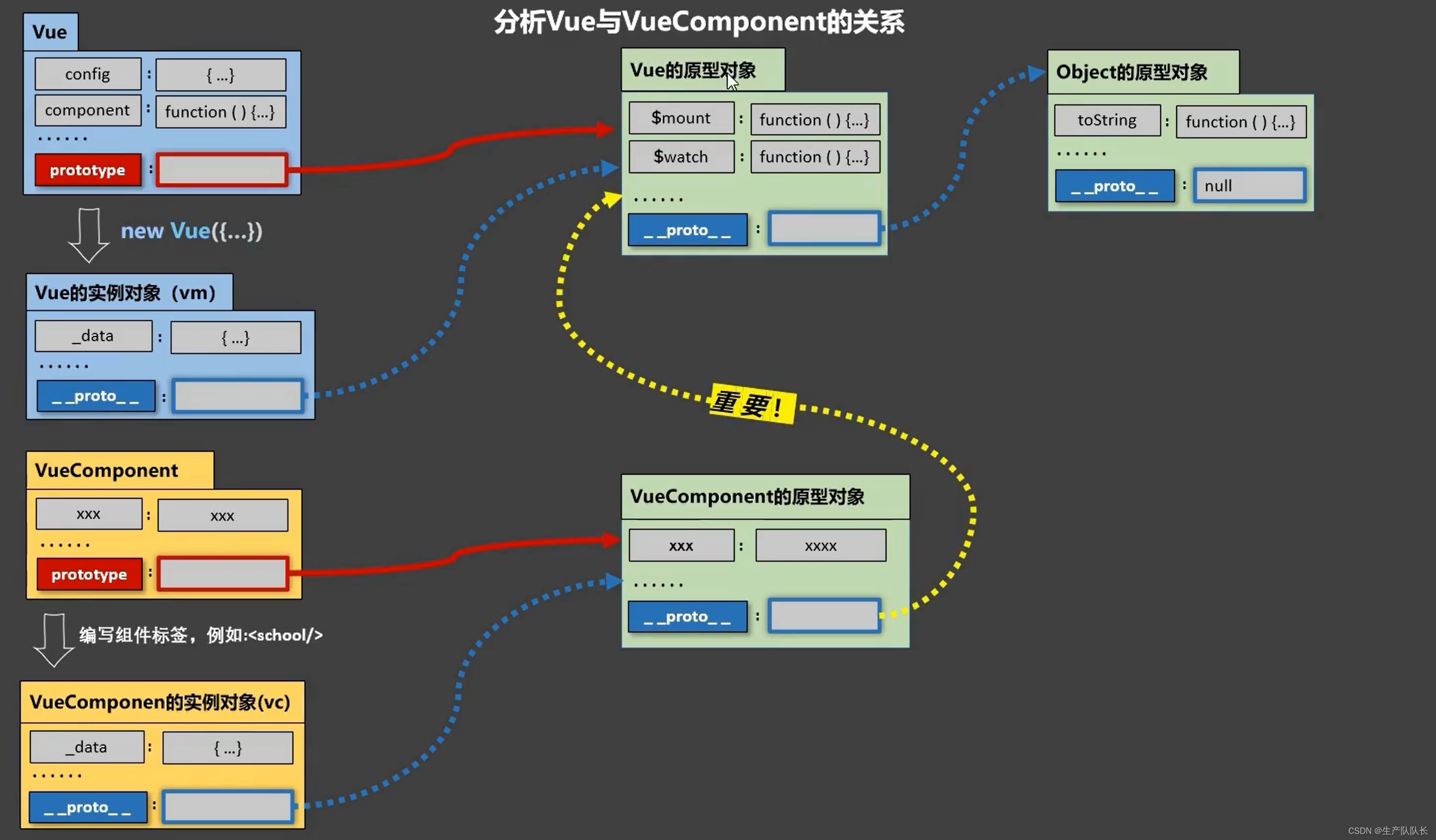
同样,这两几乎也是被淘汰了的算法,尽管它们是稳定的,但是时间复杂度没人喜欢,了解一下就好,没啥好说的,注意最后一句话就行了
一,冒泡排序
1. 算法步骤
共n-1趟,谁两敢冒泡就换了谁两
第一趟,比较n-1次,每个相邻的位置都比较一次,比较两个元素大小,若位置反了就交换位置,一趟结束,最后一个位置就是最大值(降序就是最小值)
第二趟,比较n-2次,同上,最后一个元素不参与比较
第三趟,比较n-1次,同上,最后两个元素不参与比较
……
第n-1趟,比较1次,同上,最后n-2个元素不参与比较
一共比较累 1+2+3+……n-1 = (1 + n-1)*(n-1) / 2 = 1/2 * ( n^2 - n) ,比选择排序的n^2好一点点呵,然并……
2. 动图演示
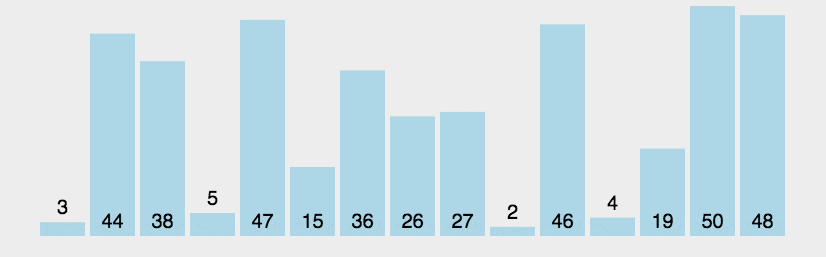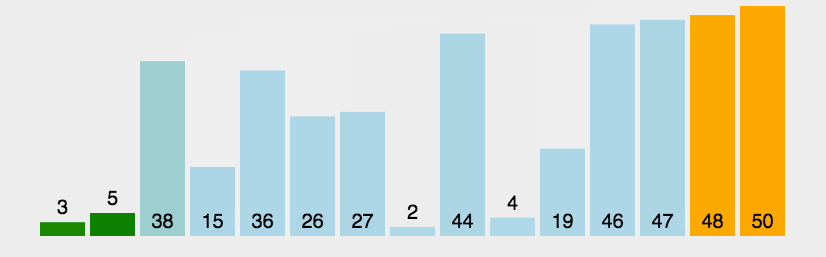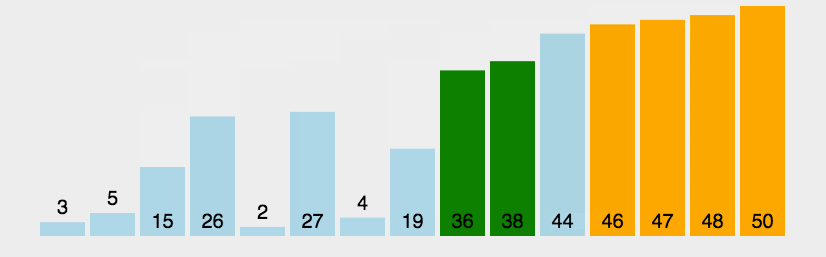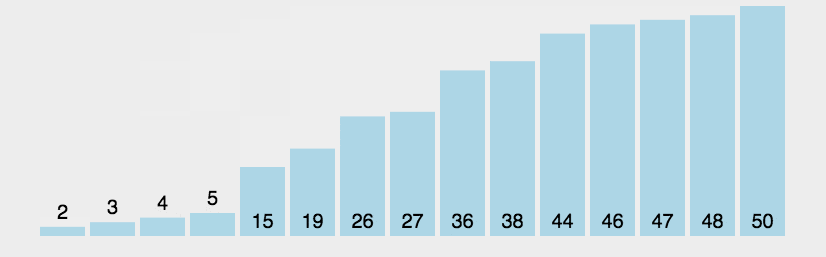
3. 什么时候最快
当输入的数据已经是正序时(都已经是正序了,我还要你冒泡排序有何用啊)。
4. 什么时候最慢
当输入的数据是反序时(写一个 for 循环反序输出数据不就行了,干嘛要用你冒泡排序呢,我是闲的吗)。
5、代码
template<typename T>
void bubble_sort(T arr[], int len) {
int i, j;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
二、插入排序
1. 算法步骤
共n-1趟,把每一个元素都插入到(理论上)原本该在的位置上去
第一趟,把第一个元素看成已经排序好了的序列,用第2个元素来与之比较,比它大就插入到第一个后面,比它小就插入到它前面 (比较1次)
第二趟,把前2个元素看成已经排序好了的序列,用第3个元素来与前面的元素逐个比较,比某个比较元素大就插入到它后面,比它小就继续比较再前一个,若直到比第一个还小,就插入到第一个的位置(比较 1~2次)
第三趟,把前3个元素看成已经排序好了的序列,用第4个元素来与前面的元素逐个比较,比某个比较元素大就插入到它后面,比它小就继续比较再前一个,若直到比第一个还小,就插入到第一个的位置(比较1~3次)
………………………………
第n-1趟,把前n-1个元素看成已经排序好了的序列,最后 1 个元素来与前面的n-1元素逐个比较,比某个比较元素大就插入到它后面,比它小就继续比较再前一个,若直到比第一个还小,就插入到第一个的位置(比较1~n-1)
比冒泡排序更好一点了,
2. 动图演示

代码实现
void insertion_sort(int arr[],int len){
for(int i=1;i<len;i++){
int key=arr[i];
int j=i-1;
while((j>=0) && (key<arr[j])){
arr[j+1]=arr[j];
j--;
}
arr[j+1]=key;
}
}特别注意:
之所以说只说是几乎被淘汰了,而不是完全淘汰,是因为这两哥们的最好情况是O(n),还都是稳定的排序方法,在元素大部分都是有序的,只有极个别的位置错了的情况下,这两个算法的优势就来了,特别是插入排序,本来就是逐个插入到正确的位置上去,现在大部分都是有序的,这部相当于大部分都插入好了嘛,就剩下极个别插入一下就完事了对吧,这是其他任何排序算法都无法比拟的存在