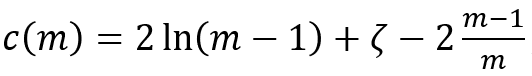小波变换

哈尔变换

对于哈尔变换可以用如下矩阵表示:
$$T=HF{H}^T$$
其中，$F$为一个$N\times N$大小的图像矩阵，$H$为一个$N\times N$大小的哈尔变换矩阵，$T$一个$N\times N$大小的图像变换的结果

对于哈尔变换矩阵$H$包含了哈尔基函数$h_k(z)$，其中$k$代表$H$的第$k$行，其中$k$满足$k=2^p+q-1$，其中$p=\lceil \ln k\rceil ,0⩽p⩽n-1,1⩽q⩽2^p$。$N=2^n$

其中哈尔基函数为
$$\begin{array}{rl}{h}_0(z)& =h_{00}(z)=\frac{1}{\sqrt{N}},z\in \left[0,1\right]\\ & \\ h_k\left(z\right)& =h_{pq}\left(z\right)=\frac{1}{\sqrt{N}}\{\begin{array}{ll}{2}^{p/2},& (q-1)2^p⩽z<(q-0.5)/z^p\\ -2^{p/2},& (q-0.5)2^p⩽z<q/2^p\\ 0,& \text{其他},z\in \left[0,1\right]\end{array}\end{array}$$
$N\times N$ 哈尔变换矩阵的第 $i$ 行包含了元素 $h_i(z)$,其中 $z=0/N,1/N,2/N,\cdots ,(N-1)/N$

即
$${\mathbf{H}}_N=[\begin{array}{cccc}{h}_0(0/N)& h_0(1/N)& \cdots & h_0(N-1/N)\\ h_1(0/N)& h_1(1/N)& \cdots & h_1(N-1/N)\\ ⋮& ⋮& \ddots & ⋮\\ h_{N-1}(0/N)& h_{N-1}(1/N)& \cdots & h_{N-1}(N-1/N)\end{array}]$$
设N=4，则
$$\begin{array}{ccc}k& p& q\\ 0& 0& 0\\ 1& 0& 1\\ 2& 1& 1\\ 3& 1& 2\end{array}$$
那么4×4 变换矩阵$H_4$为
$${\mathbf{H}}_4=\frac{1}{\sqrt{4}}[\begin{array}{cccc}1& 1& 1& 1\\ 1& 1& -1& -1\\ \sqrt{2}& -\sqrt{2}& 0& 0\\ 0& 0& \sqrt{2}& -\sqrt{2}\end{array}]$$
可知$k$可以确定$p,q$的大小，既可以确定非零值的位置范围的长度

尺度函数

设存在函数
$${\phi }_{j,k}(x)=2^{j/2}\phi (2^{j}x-k)$$
对所有的$j$, $k\in \mathbb{Z}$ 和 $\phi (x)\in L^2(R)$都成立。其中$k$ 决定了${\phi }_{j,k}(x)$ 沿$x$轴的位置，$j$ 决定了${\phi }_{j,k}(x)$ 的宽度,即它沿 $x$ 轴宽或窄。项 2${}^{\frac{j}{2}}$控制函数的幅度。由于${\phi }_{j,k}(x)$ 的形状随 $j$ 发生变化，所以 $\phi (x)$称为尺度函数。

设存在一个特定的值$j_0$，则可以得到集合 { φ j 0 , k ( x ) } \{\varphi_{j_0,k}(x)\} {φj0​,k​(x)}是集合 { φ j , k ( x ) } \{\varphi_{j,k}(x)\} {φj,k​(x)}的一个子集。其中可以把由${\phi }_{j_0,k}(x)$张成的向量空间定义为$V_{j_0}$，即
V j 0 = S p a n { φ j 0 , k ( x ) } ‾ V_{j0}=\overline{{\mathop{\mathrm{Span}}\left\{\varphi_{j_0,k}(x)\right\}}} Vj0​=Span{φj0​,k​(x)}​
若$f(x)$在${\phi }_{j_0,k}(x)$张成的空间中，则可以表示为
$$f(x)=\sum _k{\alpha }_k{\phi }_{j_0,k}(x)$$
更一般地，对于任何$j$，我们将$k$上跨越的子空间表示为

V j = S p a n { φ j , k ( x ) } ‾ V_{j}=\overline{{\mathrm{Span}\{\varphi_{j,k}(x)\}}} Vj​=Span{φj,k​(x)}​
由于$j$决定了${\phi }_{j,k}(x)$的宽或窄，即可以在x轴上表达更精细的特征，所以存在高分辨率的图像可以表示低分辨率的图像，即存在
$$V_{-\infty }\subset \cdots \subset V_{-1}\subset V_0\subset V_1\subset V_2\subset \cdots \subset V_{\infty }$$

其中 V − ∞ = { 0 } , V ∞ = { L 2 ( R ) } V_{-\infty}=\left\{0\right\},V_{\infty}=\left\{L^{2}(R)\right\} V−∞​={0},V∞​={L2(R)}

因为${\phi }_{j,k}(x)=2^{j/2}\phi (2^{j}x-k)$，所以可得${\phi }_{j+1,k}(x)=2^{(j+1)/2}\phi (2^{j+1}x-k)$

因为低分辨率的图像可以由高分辨率的图像所表示，所以存在
$${\phi }_{j,k}(x)=\sum _n{h}_{\phi }(n)2^{(j+1)/2}\phi (2^{j+1}x-n)$$
若$j,k=0$，则可以写成
$$\phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n)$$
该递归等式中的系数 $h_{\phi }(n)$称为尺度函数系数； $h_{\phi }$ 为尺度向量。

其中简单尺度函数应符合多分辨率分析的四个条件

1. **MRA要求1：**其中对于不同整数平移的简单尺度函数应是正交的
2. **MRA要求2：**低尺度函数跨越的子空间应嵌入到高尺度跨越的子空间内
3. **MRA要求3：**唯一对于所有$V_j$的通用的函数是$f(x)=0$
4. **MRA要求4：**任何函数都可以任意精度表示

小波函数

定义小波函数$\psi \left(x\right)$为$V_{j+1}$与$V_j$之差，其中
$${\psi }_{j,k}(x)=2^{j/2}\psi (2^{j}x-k)$$
其中尺度函数与小波函数的关系如下图所示

其中 W j = S p a n { ψ j , k ( x ) } ‾ W_{j}=\overline{{\mathrm{Span}\{\psi_{j,k}(x)\}}} Wj​=Span{ψj,k​(x)}​，所以存在$V_{j+1}=V_j\oplus W_j$

其中，$\oplus$ 表示空间的并集(类似于集合的并集)。$V_{j+1}$ 中$V_j$的正交补集是$W_j$, 且$V_j$中的所有成员对于$W_j$中的所有成员都正交。因此，

$$⟨{\phi }_{j,k}(x),{\psi }_{j,l}(x)⟩=0$$

对所有适当的$j,k,l\in \mathbb{Z}$都成立。

索引可以将所有可度量的、平方可积的函数空间表示为

$$L^2(R)=V_0\oplus W_0\oplus W_1\oplus \cdots$$

$$L^2(\mathbf{R})=V_1\oplus W_1\oplus W_2\oplus \cdots$$

$$L^2(\mathbf{R})=\cdots \oplus W_{-2}\oplus W_{-1}\oplus W_0\oplus W_1\oplus W_2\oplus \cdots$$

上述表达排除了尺度函数，仅采用小波进行表示

于是存在
$$L^2(\mathbf{R})=V_{j_0}\oplus W_{j_0}\oplus W_{j_0+1}\oplus \cdots$$

其中$j_0$是任意开始尺度。

因为小波空间位于相邻的较高分辨率的尺度空间中，即$W_i\subset V_{i+1}$，所以任何小波函数可以使用尺度函数表示，即
$$\psi (x)=\sum _n{h}_{\psi }(n)\sqrt{2}\phi (2x-n)$$

其中$h_{\psi }(n)$被称为小波函数系数

因为整数小波彼此正交，且与他们的互补尺度函数正交，所以存在
$$h_{\psi }(k)={\left(-1\right)}^k{h}_{\phi }(1-k)$$

一维小波变换

因为存在$L^2(\mathbf{R})=V_{j_0}\oplus W_{j_0}\oplus W_{j_0+1}\oplus \cdots$，所以存在$f(x)$可以在子空间$V_{j_0}$中用尺度函数展开和在子空间$W_{j_0}{W}_{j_{0+1}},\cdots$中用某些数量的小波函数展开来表示。即

$$f(x)=\sum _k{c}_{j_0}(k){\phi }_{j_0,k}(x)+\sum _{j=j_0}^{\infty }\sum _k{d}_j(k){\psi }_{j,k}(x)$$
其中 $j_0$ 是任意的开始尺度，$c_{j_0}(k)$通常称为近似和或尺度系数，$d_j(k)$称为细节和或小波系数。

由于双正交的性质可得
$$\begin{gathered} c_{j_0}(k)=⟨f(x),{\phi }_{j_0,k}(x)⟩=\int f(x){\phi }_{j_0,k}(x)\mathrm{d}x \\ {d}_j(k)=⟨f(x),{\psi }_{j,k}(x)⟩=\int f(x){\psi }_{j,k}(x)\mathrm{d}x \end{gathered}$$
转换成离散形式可得
$$\begin{array}{rl}{W}_{\phi }(j_0,k)& =\frac{1}{\sqrt{M}}\sum _{n}f(n){\phi }_{j_0,k}(n)\\ W_{\psi }(j,k)& =\frac{1}{\sqrt{M}}\sum _{n}f(n){\psi }_{j,k}(n),j\ge j_0\end{array}$$
其中 ${\phi }_{j_0,k}(n)$ 和${\psi }_{j,k}(n)$是基函数${\phi }_{j_0,k}(x)$ 和${\psi }_{j,k}(x)$ 的取样形式。

由此可得
$$f(n)=\frac{1}{\sqrt{M}}\sum _k{W}_{\phi }(j_0,k){\phi }_{j_0,k}(n)+\frac{1}{\sqrt{M}}\sum _{j=j_0}^{\infty }\sum _k{W}_{\psi }(j,k){\psi }_{j,k}(n)$$
通常$j_0=0$，$M$为2 的幂(即$M=2^j)$

而对于哈尔小波，离散的尺度和小波函数与$M\times M$哈尔矩阵的行相对应，其中最小尺度为0，最大尺度为$j-1$

快速小波变换

对于图像的多分辨率变换
$$\phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n)$$
并进行尺度化与平移操作，可得
$$\begin{array}{rl}\phi (2^{j}x-k)& =\sum _n{h}_{\phi }(n)\sqrt{2}\phi \left(2(2^{j}x-k)-n\right)\\ & =\sum _m{h}_{\phi }(n)\sqrt{2}\phi (2^{j+1}x-2k-n)\end{array}$$
令$m=2k+n$，可得
$$\begin{array}{r}\begin{array}{rl}\phi (2^{j}x-k)& =\sum _n{h}_{\phi }(n)\sqrt{2}\phi \left(2(2^{j}x-k)-n\right)\\ & =\sum _m{h}_{\phi }(n)\sqrt{2}\phi (2^{j+1}x-2k-n)\\ & =\sum _m{h}_{\phi }(m-2k)\sqrt{2}\phi (2^{j+1}x-m)\end{array}\end{array}$$
同理对于小波函数存在
$$\psi (2^{j}x-k)=\sum _m{h}_{\psi }(m-2k)\sqrt{2}\phi (2^{j+1}x-m)$$
其中将${\psi }_{j,k}(x)=2^{j/2}\psi (2^{j}x-k)$代入$d_j(k)=⟨f(x),{\psi }_{j,k}(x)⟩=\int f(x){\psi }_{j,k}(x)\mathrm{d}x$可得
$$d_j(k)=\int f(x)2^{j/2}\psi (2^{j}x-k)\mathrm{d}x$$
又因为$\psi (2^{j}x-k)={\sum }_m{h}_{\psi }(m-2k)\sqrt{2}\phi (2^{j+1}x-m)$

所以存在
$$\begin{array}{rl}{d}_j(k)& =\int f(x)2^{j/2}[\sum _m{h}_{\psi }(m-2k)\sqrt{2}\phi (2^{j+1}x-m)]\mathrm{d}x\\ & =\sum _m{h}_{\psi }(m-2k)[\int f(x)2^{(j+1)/2}\phi (2^{j+1}x-m)\mathrm{d}x]\\ & =\sum _m{h}_{\psi }(m-2k)c_{j+1}(m)\end{array}$$
同理可得
$$c_j(k)=\sum _m{h}_{\phi }(m-2k)c_{j+1}(m)$$
即
$$\begin{array}{rl}{W}_{\psi }(j,k)& =\sum _m{h}_{\psi }(m-2k)W_{\phi }(j+1,m)\\ W_{\phi }(j,k)& =\sum _m{h}_{\phi }(m-2k)W_{\phi }(j+1,m)\end{array}$$
上式揭示了相邻尺度直接的离散小波变换(DWT)系数之间的关系，可以认为是$W_{\phi }(j+1,m),W_{\psi }(j+1,m)$分别与$h_{\phi }(-n),h_{\psi }(-n)$进行卷积操作并下采样得到的，于是可以写成
$$\begin{gathered} W_{\psi }(j,k)=h_{\psi }(-n)\star W_{\varphi }(j+1,n){|}_{n=2k,k⩾0} \\ {W}_{\phi }(j,k)=h_{\phi }(-n)\star W_{\phi }(j+1,n){|}_{n=2k,k⩾0} \end{gathered}$$
即如下图所示的结构

同时可以经过多次迭代分解，如下图是二级分解的结构

二维小波变换

为了将小波变换扩展到适应二维的图像，由此定义，存在尺度函数
$$\phi (x,y)=\phi (x)\phi (y)$$
以及三个对方向敏感的小波函数
$$\begin{array}{rl}& {\psi }^H(x,y)=\psi (x)\phi (y)\\ & {\psi }^V(x,y)=\phi (x)\psi (y)\\ & {\psi }^D(x,y)=\psi (x)\psi (y)\end{array}$$
以上三个小波函数分别对应图像沿着列方向的变换、图像沿着行方向的变换、图像沿着对角线方向的变换

并存在
$$\begin{array}{c}{\phi }_{j,m,n}(x,y)=2^{j/2}\phi (2^{j}x-m,2^{j}y-n)\\ {\psi }_{j,m,n}^i(x,y)=2^{j/2}{\psi }^i(2^{j}x-m,2^{j}y-n),i=\{H,V,D\}\end{array}$$
并可以推导出离散形式的小波变换
W φ ( j 0 , m , n ) = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) φ j 0 , m , n ( x , y ) W ψ i ( j , m , n ) = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) ψ j , m , n i ( x , y ) , i = { H , V , D } \begin{aligned} W_{\varphi}(j_{0},m,n)&=\frac{1}{\sqrt{MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\varphi_{j_{0},m,n}(x,y)\\\\ W_{\psi}^{i}(j,m,n)&=\frac{1}{\sqrt{MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\psi_{j,m,n}^{i}(x,y),i=\{H,V,D\}\end{aligned} Wφ​(j0​,m,n)Wψi​(j,m,n)​=MN ​1​x=0∑M−1​y=0∑N−1​f(x,y)φj0​,m,n​(x,y)=MN ​1​x=0∑M−1​y=0∑N−1​f(x,y)ψj,m,ni​(x,y),i={H,V,D}​
其中$j_0$表示任意的开始尺度，$W_{\phi }(j_0,m,n)$表示在尺度为$j_0$时的近似， W ψ i ( j , m , n ) , i = { H , V , D } W_{\psi}^{i}(j,m,n),i=\{H,V,D\} Wψi​(j,m,n),i={H,V,D}表示对尺度为$j_0$时的水平、垂直与对角线方向的细节

当$j_0=0,M=N=2^j$时，存在离散小波逆变换
$$\begin{array}{rl}f(x,y)& =\frac{1}{\sqrt{MN}}\sum _m\sum _n{W}_{\phi }(j_0,m,n){\phi }_{j_0,m,n}(x,y)\\ & +\frac{1}{\sqrt{MN}}\sum _{i=H.V.D}\sum _{j=j_0}^{\infty }\sum _m\sum _n{W}_{\psi }^i(j,m,n){\psi }_{j,m,n}^i(x,y)\end{array}$$
同理可以得到

小波分解过程如图所示

小波逆变换过程如图所示

其小波分解的结果如图所示