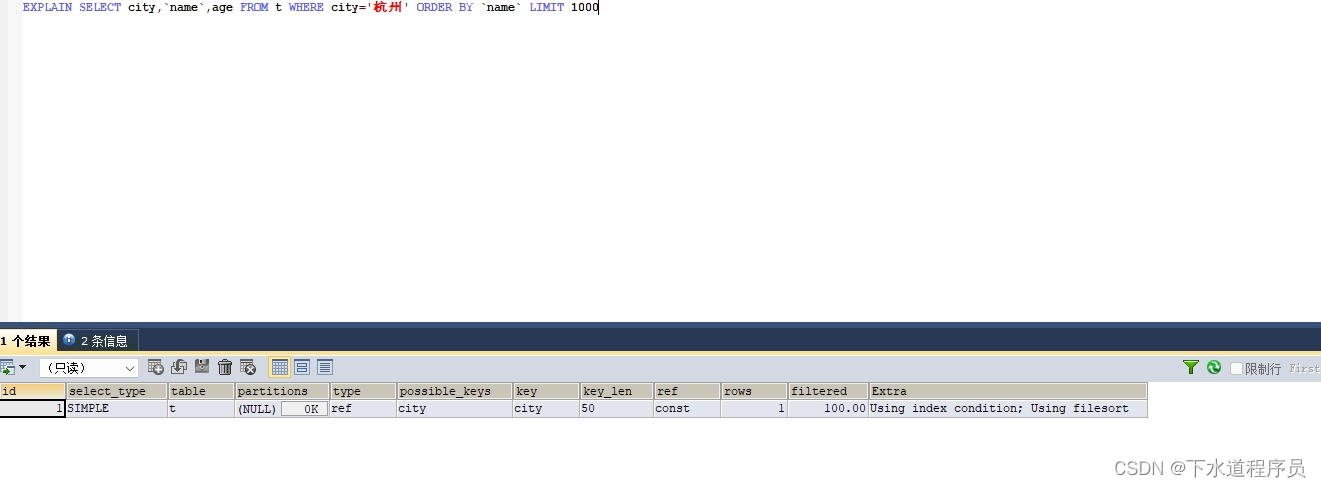
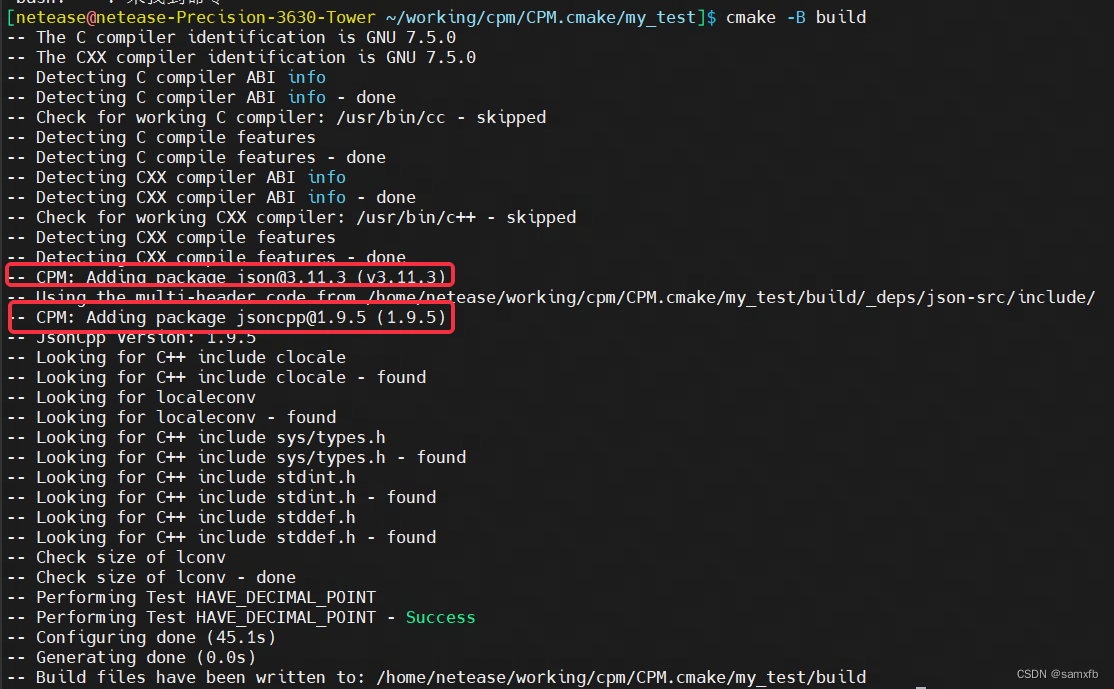
一、向量、矩阵范数与谱半径

【数值计算方法（黄明游）】解线性代数方程组的迭代法（一）：向量、矩阵范数与谱半径【理论到程序】

1. 向量范数

• $l_1$ 范数（曼哈顿范数）：
  $$||x|{|}_1=\sum _{i=1}^n|x_i|$$

• $l_2$ 范数（欧几里得范数）：
  $$||x|{|}_2=\sqrt{\sum _{i=1}^n{x}_i^2}$$

• $l_{\infty }$ 范数（无穷范数）：
  $$||x|{|}_{\infty }=\underset{1\le i\le n}{\max }|x_i|$$

2. 矩阵范数

• 弗罗贝尼乌斯范数（矩阵中每项数的平方和的开方值）
  $$||A|{|}_F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n|a_{ij}{|}^2}$$
• 算子范数
  • 行和范数：当 $p=\infty$ 时，算子范数被定义为矩阵中各行元素按绝对值求和所得的最大和数，即，
    $$||A|{|}_{\infty }=\underset{1\le i\le n}{\max }\sum _{j=1}^n|a_{ij}|$$
  • 列和范数：当 $p=1$ 时，算子范数被定义为
    矩阵列的绝对值之和的最大值。即，
    $$||A|{|}_1=\underset{1\le j\le n}{\max }\sum _{i=1}^n|a_{ij}|$$
  • 当 $p=2$ 时，算子范数即$A$ 的谱半径,谱半径是矩阵的特征值的按模最大值
    $$||A|{|}_2=\sqrt{{\lambda }_{\text{max}}(A^{T}A)}=p(A)=\max |\lambda |$$

3. 谱半径

  谱半径是矩阵的特征值按模最大的那个值，对于一个 $n\times n$ 的矩阵 $A$，其谱半径 $p(A)$ 定义为：

p ( A ) = max ⁡ { ∣ λ ∣   ∣   λ  是  A  的特征值 } p(A) = \max \{|\lambda| \ | \ \lambda \text{ 是 } A \text{ 的特征值}\} p(A)=max{∣λ∣ ∣ λ 是 A 的特征值}

二、迭代法的一般形式与收敛性定理

待完善……