第6章 上的 Fourier 变换
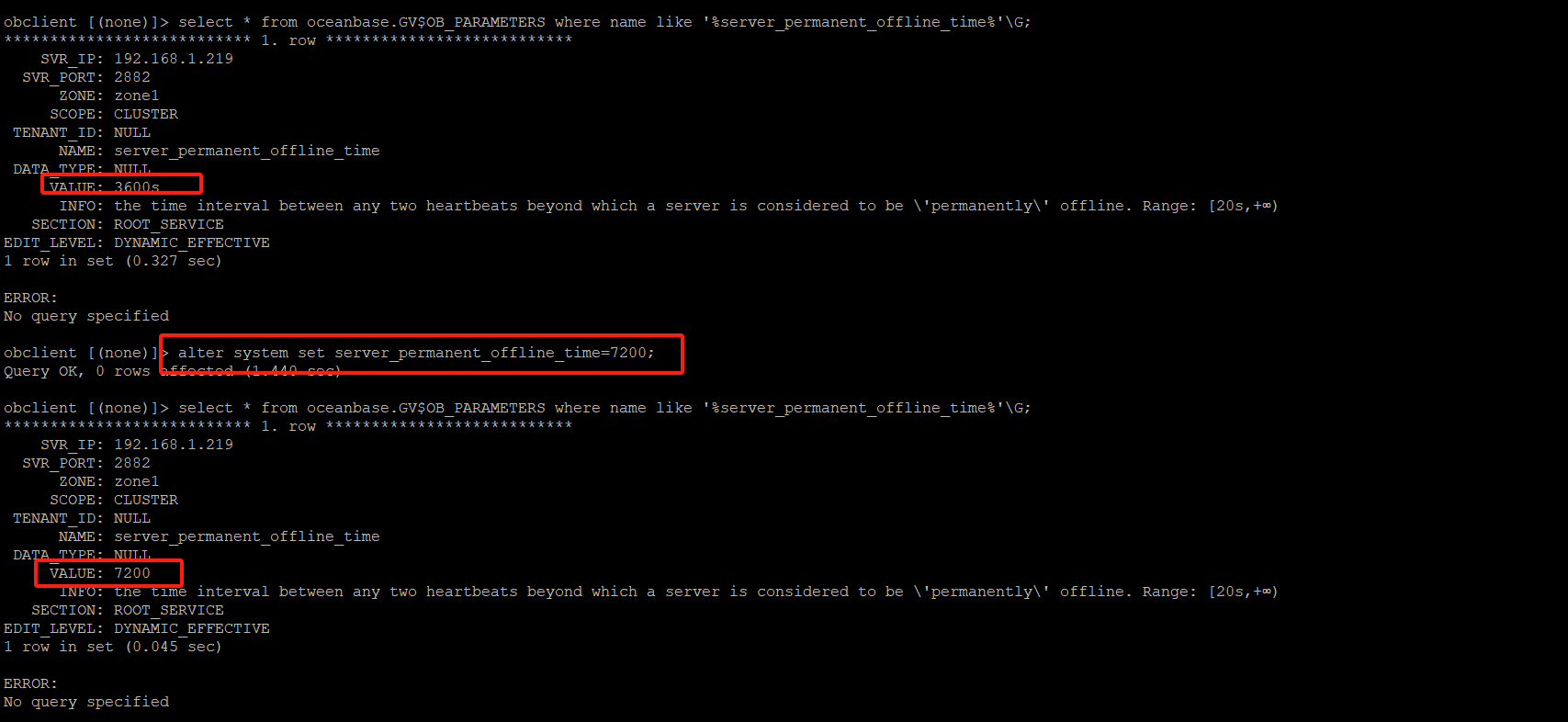
It occurred to me that in order to improve treatment
planning one had to know the distribution of the at-
tenuation coefficient of tissues in the body. This in-
formation would be useful for diagnostic purposes and
would constitute a tomogram or series of tomograms.
It was immediately evident that the problem was
a mathematical one. If a fine beam of gamma rays
of intensity is incident on the body and the emerg-
ing density is I, then the measurable quantity g equals
, where f is the variable absorption
coefficient along the line L. Hence if f is a function of
two dimensions, and g is known for all lines intersect-
ing the body, the question is, can f be determined if
g is known? Fourteen years would elapse before I learned that
Radon had solved this problem in 1917.
( 我突然想到,为了改进治疗计划,人们必须了解体内组织衰减系数的分布。 该信息对于诊断目的非常有用,并将构成断层照片或一系列断层照片。很明显,这个问题是一个数学问题。 如果一束强度为 的 Γ 射线入射到物体上,出射密度为 I,,则可测量的量 g 等于
,其中 f 是沿线 L 的可变吸收系数。因此,如果 f 是二维函数,并且已知所有与身体相交的线的 g,那么问题是,如果已知 g,是否可以确定 f ?
十四年后,我才知道 Radon 在 1917 年解决了这个问题。
-----------------------------------------------------------------------------A. M. Cormack, 1979----------------
前一章介绍了 ℝ 上的Fourier变换理论,并展示了它在偏微分方程中的一些应用。 在这里,我们的目标是为多个变量的函数提出一个类似的理论。
在简要回顾了 中的一些相关概念之后,我们将从一些关于 Schwartz 空间
上的Fourier变换的常见事实开始。幸运的是,主要思想和技术已经在一维案例中得到了考虑。事实上,使用恰当的记法,关键定理的表述(和证明)(例如逆 Fourier 变换和 Plancherel 公式)可保持不变。
接下来,我们强调与数学物理中一些高维问题的联系,特别是研究 d 维的波动方程,并在 d = 3 和 d = 2 的情况下进行详细分析。在这个阶段,我们发现了大量的Fourier 变换和旋转对称(rotational symmetry)之间的相互作用,这只有在 中当 d ≥ 2 时才会出现。最后,本章将以对 Radon 变换的讨论结束。 这个主题本身就很有趣,但除此之外,它在 X 射线扫描的使用以及数学的其他部分的应用中也具有重要的相关性。
1. 预备知识(Preliminaries)
本章的背景(setting)将是 ——实数 d 元组
构成的向量空间(参见第3章对向量空间和内积的简短回顾。在这里,我们发现使用小写字母(例如 x (相对于X ))分配
中的点更为方便。此外,我们使用|.|而不是||.||表示Euclid范数(norm))。向量的加法是逐分量相加,且乘法也是按实数标量逐分量进行的标量乘。已知
,我们定义
,
因此,| x |只是以常规Euclid范数表示的向量 x 的长度。我们为 配备标准的内积,定义为
,
因此, 。我们用记法 x.y 替换掉第3章中的记法 ( x, y )。
已知一个非负整数的 d 元组 (有时称为一个多下标组(multi-index))(译注:多下标组数符号是一种数学符号,通过将整数下标的概念推广到有序的索引元组,它简化了多变量微积分、偏微分方程和分布理论中使用的公式),单项式(monomial)
定义为
。
类似地,我们定义微分算子(或称微分算符,differential operator) 为
,
其中, 是多下标组 α 的阶(order)。
1.1 对称性(symmetries)
中的分析,特别是应用 Fourier变换理论分析,是由底层空间的三个重要对称群(group)塑造的(is shaped):
(i) Translations(平移群)
(ii) Dilations(扩张群)
(iii) Rotations(旋转群)
我们已经看到,平移 (
固定 ) , 和扩张 x ⟼δx (δ > 0) 在维理论的分析中起着重要的作用。在 ℝ 中,仅有的两个旋转是采用 -1 的恒等式和乘法。然而,在
中当 d≥ 2 时会有更多的旋转,对Fourier变换和旋转之间相互作用的理解导致对球面对称性的富有成果的洞察。
上的旋转是一个线性变换——
,它保留了内积。换句话说,
(对于所有
和
) 。
(对于所有
) 。
等价地,最后的条件可以替换为 (对于所有
),或替换为
(其中,
和
分别表示 R 的转置(transpose)和逆(inverse)) (注:回顾一下,一个线性算子
是满足这样条件的线性算子
——对所有
,有
。我们写作,
。A 的逆(当它存在的情况下)是线性算子
且 A ∘C = C ∘A = I (其中,I是恒等运算), 我们写作
) 。特别是,我们有 det(R) = ±1,其中,det(R)是 R 的 方阵或行列式(determinant)。如果 det(R) = 1,我们称 R 是一个真旋转(proper rotation);否则,我们称R 是一个伪旋转(improper rotation)。
例子1:
在实数轴 ℝ 上,存在两个旋转:恒等式(identity)是真旋转,采用-1的乘是伪旋转。
例子2:我们通过将点 (x,y) 赋予复数 z = x + i y 的方式来表示复数 ℂ ,再用 ℂ 来表征 。
在这个恒等式下,所有的真旋转是对于某些 φ∈ℝ 具有形如 的变换,而所有的伪旋转是对于某些 φ∈ℝ 具有形如
的变换(此处,
表示 z 的复数共轭)(见练习1关于导出这个结论的论据)。
例子3:
Euler给出了 中旋转的极其简单的几何描述。即,已经一个真旋转 R , 存在一个单位向量 𝛾 使得:
(i) R 锁定 𝛾,即,R (𝛾) = 𝛾 。
(ii) 假如 𝒫 表示经过原点与 𝛾 垂直的平面,则,R :𝒫 ⟶ 𝒫 ,且 R 到 𝒫 的约束是
中的一个旋转。
在几何上,向量 𝛾 给出了旋转由的方向。这个事实的证明在练习2中给出。最后,假如 R 是伪旋转,则 -R 是真旋转(因为,在 中 , det(-R) = -det(R)),因此,R 是真旋转和关于原点对称的组合。
例子 4:已知 中的正交基
和
, 我们可以通过令
的方式定义旋转R。反之,如果 R 是一个旋转而
是一个正交基,则
(i = 1,...,d ) 是另一个正交基。
1.2 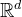 (R^d) 上的积分(Integration on
(R^d) 上的积分(Integration on 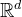 (R^d) )
(R^d) )
由于我们将要处理 上的函数,我们将必须讨论这样的函数的积分的某些方面。
上更详细的积分回顾在附录中给出。
对于 上一个连续的复数值函数 f ,如果对于每一个多下标元组 α, 函数
都是有界的,则称函数 f 是寁(zǎn)降的(rapidly decreasing)。等价地,对于
上一个连续的复数值函数 f ,如果对于每一个 k = 0,1,2,... ,有
,
则称函数 f 是寁降的。已知一个寁降函数,我们定义
,
其中, 表示中心在原点的闭合立方体,且长度为 N 的边平行于坐标轴,即,
。
在常规的Riemann积分的意义上, 上的积分是多重积分。从这个事实——积分
随着 N 趋近于无穷大而构成Cauchy序列,可以推导出极限存在。
我们先后有两个观察。第一,我们可以用球(ball) 替换立方体
而无需改变其定义。第二,我们无需使用寁降的全部力量来证明极限的存在。事实上,假设 f 是连续函数,且对于某些 𝜀 > 0,有
,
这就足以证明 f 极限的存在。例如,ℝ上中速递降函数对应于 𝜀 = 1 的函数。为了与此保持一致,我们将 上的中速递降函数定义为连续且满足以上 𝜀 = 1 时的不等式的函数。
积分与三个重要对称群的相互作用如下:假如 f 是中速递降的,则,
( i ) ( 对所有
) ,
(ii) ( 对所有 δ > 0 ) ,
(iii) (对每一个旋转R ) 。
极坐标(Polar coordinates)
在 中引入极坐标,求得相应的积分公式会很方便。我们以两个例子开始,它们分别对应 d = 2 和 d = 3 这两种情况(适用于所有 d 的更详尽的讨论包含在附录中)。
例子1:
在 中,极坐标由( ρ, θ)( ρ ≥ 0 且 0 ≤ θ ≤ 2π)给出。变量替换的Jacobian矩阵等于r,因此,
。
现在,我们可以将单位圆周上的某一点 写为
,且给出圆周上的函数 g ,我们定义其沿
的积分为
。
对于这个记法,则我们有
。
例子2:
在 中,我们使用如下球面坐标
其中,0 < r,0 ≤ θ ≤ π 且 0 ≤ φ ≤ 2π 。变量替换的Jacobian矩阵 ,因此,
。
假如 g 是一个位于单位球面 且
, 我们可以定义表面元素 dσ(𝛾)为
。
因此,
。
通常,将 中的任意点唯一地写成
是可行的。其中 𝛾 取决于单位球体 且 r > 0 。事实上,可取 r = | x | 且 𝛾 = x / | x | 。因此,人们可以像 d = 2 或 d = 3 的情况一样继续定义球坐标。我们将使用的公式是
(只要 f 是寁降的)。
这里,dσ(𝛾) 表示可以从球面坐标中获得的基于球面 的表面元素。
2. Fourier变换的基本理论(Elementary theory of the Fourier transform)
Schwartz 空间 (有时候缩写为
) 由
上使得
对于每一个多下标组 α 和 β 都成立的所有无限可微函数f 构成。换句话说,f 及其所有的导数都要求是寁降的。
例子1: 中的一个函数例子就是,由
给出的 d 维Gauss函数。第5章的理论已经清晰地阐述了在 d = 1 的这种情况下,这个函数所起的核心作用。
Schwartz函数 f 的Fourier变换定义为
( 对于
) 。
注意,现在除了我们是在 上进行积分之外,这个公式与一维Fourier变换公式是相似的,并且 x 和ξ 的乘积被两个向量的内积所取代。
现在,我们列出一些Fourier变换的简单属性,在下面的命题中,右向的箭头表示我们已经执行了Fourier变换,因此, 意味着
。
命题 2.1 令 。
( i ) ( 只要 h ∈ ℝ ) 。
( ii ) ( 只要 h ∈ ℝ ) 。
( iii ) ( 只要 h ∈ ℝ ) 。
( iv ) 。
( v ) 。
( vi ) (只要 R 是旋转的)。
前面五个属性可以按与证明一维的五个属性的方式加以证明。为了证明最后一个属性,在积分式中简单地作变量替换 y = Rx 。然后,回顾事实 |det(R)| = 1 ,并且 R 是旋转的,因此有 。
命题中的 ( iv ) 和 ( v ) 表明,取决于 2πi 因子,Fourier变换按单项式(monomials)交换微分和乘法。这激发了对 Schwartz 空间的定义并导出了下一个推论。
推论 2.2 Fourier变换将 空间映射到自身。
在这一点上,我们离题(digress)观察一个关于Fourier变换和旋转之间相互作用的简单事实。 如果一个函数 f 仅依赖于 |x|,我们称它是一个径向函数(radial function)(译注:沿半径或直径的直线方向;径向是相对的,如一个轴,必须会有轴心,而垂直于轴的中心线的任何方向,均可以称为径向;而垂直于轴的中心线的任何平面,称为径向平面);换句话说,假如存在一个函数 ,定义,对于 u ≥ 0 ,使得
。我们注意到,对于每一个旋转R ,当且仅当 f (Rx ) = f ( x ) 时,f 是径向的。在一个方向上,这是很明显的,因为 | Rx |=| x |。相反,假如 f (Rx ) = f ( x ),对于缺有的旋转 R ,现在定义
为
。
注意, 是良好定义的,因为,假如 x 和 x ’是具有| x |=| x’| 的点,总是存在一个点使得 x’= Rx 。
推论 2.3 径向函数的Fourier变换也是径向函数。
从最后一个命题中的属性(vi)立即就可以推出这个推论。事实上,对于所有的R,f (Rx ) = f ( x )这个条件就意味着,对于所有的 R, 有 ,因此,只要f 是径向的, 则
便是径向的。
中径向函数的一个例子便是Gauss函数
。此外,我们观察到,当 d = 1 时, 径向函数恰好是一个偶函数,即,满足 f ( x ) = f ( -x )的那类函数。
在这些学习了这些预备知识之后,我们回溯上一章的步骤,得到 的逆Fourier公式和 Plancherel定理。
定理 2.4 假如 。则,
。
此外,
。
证明按下面的步骤进行。
第一步:Gauss函数 的Fourier变换是
。为了证明这一点,注意到指数函数的属性,意味着
和
,
因此,在Fourier变换中的积分是 d 个函数的积,其中,每一个函数仅取决于变量 。因此,通过将
上的积分写成一系列重复的积分,每个积分都接管 ℝ,就推出了这个论断。例如,当 d = 2 时,
。
应用命题2.1的一个结论,用 替代 δ ,我们求得
。
第二步:族 是
中的一个好核族。根据好核族的标准,我们指的是
( i ) ,
( ii ) (事实上,
) ,
(iii) 对于每一个 η > 0 , (当 δ ⟶ 0 时 ) 。
这些诊断的证明几乎与 d = 1 时的情况相同。因此,当 F 是一个Schwartz函数的时候,或者更一般地,当 F 在原点是有界且连续的时候,有
(当 δ ⟶ 0 时)。
第三步:当 f 和 g 在 𝒮 中的时候,乘法公式
。
证明要求 在
上的积分作为重复积分计算,且每个单独的积分接管
。这个论证类似与在前面章节中的命题1.8的证明(见附录)。
然后,逆 Fourier 变换只是简单地应用乘法公式与好核族 的结果,与第5章中的情况一样。此外,它还推出 Fourier变换 ℱ 是一个
映射到其自身的双射,其逆变换为
。
第四步:接下来,我们转向卷积,定义为
。
我们有 ,
, 并且
。对这个属性的论证与一维的情况相似。
的Fourier变换的积分涉及
(
之上) 作为重复积分的积分。
然后,遵循在前面章节中使用的论证方法,我们就求得了d维 Plancherel公式,从而得出定理 2.4 的证明。
3. 在 R^d ×ℝ (  ) 中的波动方程(The wave equation in R^d
) 中的波动方程(The wave equation in R^d
×ℝ)
我们的下一个目标是将我们对Fourier变换的了解应用到波动方程的研究中。 在这里,我们再次通过将自己的视野限制在 Schwartz 类 𝒮 中的函数来简化问题。我们注意到,在波动方程的任何进一步分析中,重要的是允许具有更通用行为的函数,特别是可能不连续的函数。 然而,我们通过仅考虑 Schwartz 函数失去了通用性,我们获得了透明度。我们在这种受限背景下的研究将使我们能够以最简单的形式解释某些基本思想。
3.1 依据Fourier变换求解(Solution in terms of Fourier transforms)
振动弦的运动满足方程
,
其中,我们称之为一维波动方程。这个方程到 d 维空间变量的一个自然扩展是
(1) 。
事实上,我们知道,在 d = 3 这种情况中,这个方程确定了真空中电磁波的行为(c = 光速)。此外,这个方程描述了声波的传播。因此,(1)被称为 d 维波动方程。
我们首先观察到的是,我们可以假设 c = 1,因为,如有必要,我们可以重新调节变量 t 。此外,假如我们将 d 维Laplace算子定义为
,
则,上面的波动方程可以重写为
(2) (译注:我们上面假设 c = 1) 。
本节的目标是,在初始条件
和
( 其中,
)
的约束下,求得方程的一个解。这被称为关于波动方程的 Cauchy问题。
在求解这个问题之前,我们要指出的是,当我们将变量 t 看成时间的时候,我们不能将我们自己的视野限定在 t > 0 的范围内。正如我们将会看到的那样,我们求得的解对于所有 t ∈ℝ 都有意义。这是波动方程可以在时间上反转的一个表现(不像热传导方程)。
下一个定理给出了求解我们问题的公式。得出这个公式的启发式论证很重要,因为正如我们已经看到的,它也适用于其他一些边值问题。
假设 u 是对波动方程的 Cauchy 问题的解。关于空间变量 应用的技术包括对方程及其初始条件取 Fourier变换。这样,就将求解波动方程归结为求解用时间作为自变量的常微分方程。事实上,回顾关于
的微分变成按
的乘法这个事实,以及关于 t 的微分在空间变量中与Fourier变换可交换这个事实,我们发现(2)变成
。
对于每一个固定的 ,这是另一个以 t 为自变量的常微分方程,其解由
其中,对于每一个ξ ,A(ξ ) 和 B(ξ ) 是由初始条件确定的未知常量。事实上,取初始条件的Fourier变换(按x)产生
和
。
我们现在可以对 A(ξ ) 和 B(ξ ) 求解,得到
和
。
因此,我们求得
,
方程的解 u 通过按 ξ 变量执行逆Fourier变换给出。导然,这种形式的推导引出了我们问题的精确解存在定理。
定理 3.1 波动方程Cauchy问题的一个解是
(3) 。
证明:
我们首先验证 u 是波动方程的解。一旦我们注意到,我们可以在积分符号下(因为 f和g 都是Schwartz函数)按 x 和 t 进行微分,因此,u 至少是 类,这样事情就很简单。在另一方面,我们对指数函数关于 x 变量进行(二次)微分,我们得到
,
而在另一方面,我们关于 t 二次微分方括号中的项,得到
。
这就证明了 u 是方程(2)的解。令 t = 0,根据逆Fourier变换定理,我们得到
。
最后,我们再次针对 t 进行微分,令 t = 0 ,并使用逆Fourier变换证明
。
因此,u 也验证了初始条件。定理的证明完成。
正如读者将会注意到的, 和
两者都是 𝒮 中的函数。
因为 和
两者都是可无限微分的偶函数。
在证明了波动方程的Cauchy问题解的存在性后,我们提出唯一性问题。除了定理中的公式给出的以外,是否存在
受条件
和
的约束的问题的解?
事实上,正如预期的那样,答案是否定的。 这个事实的证明,这里不会给出(但见问题 3),可以基于能量守恒论证。这是我们现在将要介绍的全局能量守恒表述的局部副本。
我们在第 3 章练习 10 中观察到,在一维情况下,振动弦的总能量随时间守恒。 这个事实的类比也适用于更高的维度。定义一个解的能量为
。
定理 3.2 假如 u是由 (3) 给出的波动方程的解,则 E(t)是能量守恒的(conserved),即,
E(t) = E(0) (对于所有 t ∈ ℝ) 。
对其证明需要下面的引理。
引理3.3 假如 a 和 b是复数而α是实数。则
。
直接就可以推导出这个等式,因为 ,
是一对正交向量,因此,复数
,我们有
,
其中,“.” 表示 中的内积。
现在,根据 Plancherel 定理,
。
类似地,
。
现在我们带着 ,
和
应用引理,结果是
,
很显然,上式独立于 t 的。因此,定理 3.2证毕。
方程式(3)虽然给出了波动方程的解,但缺点是比较间接,需要计算f和g的Fourier变换,然后再进行逆Fourier变换。 然而,对于每个维度 d,都有一个更明确的公式。当 d = 1 时这个公式非常简单,而当 d = 3 时稍微简单一些。更一般地说,只要 d 是奇数,公式就是“基础(elementary)”,而当 d 是偶数时更复杂(见问题 4 和 5)。
下面我们考虑情况 d = 1、d = 3 和 d = 2,它们一起给出了一般情况的图景。回想一下,在第 1 章中,在讨论区间 [0,L] 上的波动方程时,我们求得由d'Alembert公式给出的解
(4) 。
并且解释为,f 和 g都被延拓到区间 [0,L]之外,使它们在区间 [-L, L]上为奇函数,且在实数轴上为周期函数。对于波动方程的解而言,当 d = 1 且当初始数据是 中的函数时,公式(4)也成立。事实上,假如我们注意到
和
则我们直接可以从(3)推导出(4)。
最后,我们注意到,d'Alembert 公式 (4) 中出现的两项由适当的平均值组成。事实上,第一项恰好是 f 在闭区间 [x - t,x + t ] 的边界上两个点的平均值;第二项,取决于因子 t,是这个区间上 g 的均值,即, 。这表明了到更高维度的扩展,我们可能希望将问题的解写成初始数据的平均值。事实上就是这样,我们现在详细讨论 d = 3的特殊情况。
3.2 R^3 × ℝ ( )中的波动方程(The wave equation in R^3 ×ℝ)
)中的波动方程(The wave equation in R^3 ×ℝ)
假如 表示
中的单位球面,我们将球心位于 x 半径为 t 的球面上的函数 f 的球面均值定义为
(5) ,
其中,其中,dσγ 是对 的表面面积元素。因为 4π 是单位球面的面积,我们可将
解释为球心位于 x 半径为 t 的球面上的函数 f 的球面均值。
引理 3.4 假如 且 t 固定, 则
。此外,
按 t 是无限可微的,且每一个 t 阶导数也属于
。
证明:
令 。为了证明 F 是寁降的,我们以不等式
(对于每一个 N ≥ 0)开始。一个简单的结论是,只要 t 是固定的,我们便有
( 对所有
) 。
为了理解这一点,分别考虑当 | x |≤ 2| t | 时和 | x |≥ 2| t | 时这两种情况。因此,根据积分,有
,
且因为此式对每一个N ≥ 0 成立,所以函数 F 是寁降的。接下来,我们注意到,F 是无限可微的,且
(6) ,
其中, 。当
时,即足以证明上式,然后,继续推理,即可得到一般的情况。此外,取 k = 1 即可。现在,
,
其中, , 且
。现在,只要观察到
(当 h ⟶ 0 时,以 γ 一致地) 这一点就足够证明了。因此,我们发现 (6) 是成立的,并且,根据第一个参数,可以推断出
也是寁降的,因此, F ∈ 𝒮。同样的论据适用于
的每一个 t 阶导数。
我们需要的关于球面积分的基本事实是以下Fourier变换公式。
引理 3.5 。
正如我们将在下一节中看到的,该公式与径向函数的Fourier变换是径向的这一事实有关。
证明:
注意到,左边的积分式是按ξ径向的。事实上,假如 R 是一个旋转,因为我们可以替换变量 ,则
。
(对于这一点,参见附录中的公式(4)。) 因为 | ξ | = ρ ,用ξ = (0,0, ρ)就足以证明引理。假如ρ = 0 引理很明显。假如ρ > 0 ,我们选取球面坐标求得左侧部分等于
。
变量替换 u = -cos(θ)给到
,
因此,公式得证。
按照公式(5)的定义,我们可以将 解释为函数 f 与元素 dσ
![]() 的卷积,因为Fourier变换交换卷积与乘积,我们被引导认为,
的卷积,因为Fourier变换交换卷积与乘积,我们被引导认为, 是对应的Fourier变换的乘积。事实上,我们有恒等式
(7) 。
为了便于理解,我们写成
,
注意到,我们可以交换积分的次序,并做简单的变量替换即可实现以上恒等式。
结果,我们发现,我们问题的解可以通过使用初始数据的球面平均值来表达。
定理 3.6 当 d = 3 时,受初始条件
和
约束的波动方程 的解由
给出。
证明:
考虑第一个问题,方程 受
和
约束。则,根据定理 3.1,我们知道其解
为
,
其中,我们将(7)应用于g,并应用逆Fourier变换定理。
再次根据定理 3.1, 受初始条件 和
约束的波动方程
的解由
,
给出。
现在,我们可以叠加这两个解 , 以此作为我们原始问题的解。
Huygens 原理(Huygens principle)
一维和三维波动方程的解分别为
和
。
我们注意到,在一维问题中,位于(x,t)的解的值仅取决于中心位于x长度为2t的区间上 f 和 g 的值,如图1所示。
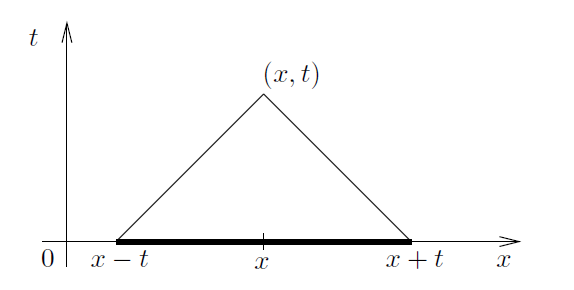
-------------------------------------------图 1 Huygens 原理,d = 1 时的情况-----------------------------------
如果另外加上 g = 0,则方程的解仅取决于在这个区间上位于边界点的数据。在三维的情况下,这个边界依赖性依然成立。更确切地说,波动方程的解 u(x,t) 仅取决于位于半径长为 t 球心位于 x 的球面上函数 f 和 g 的值。这种场景如下图 2所描绘,其中,我们已经绘制了锥点位于(x,t)且底位于半径长为t球心位于x的球上的圆锥体。这个圆锥体称为锥点位于(x,t)的反向光锥(backward light cone)。

----------------------------------------------图 2 锥点位于(x,t )反向光锥-------------------------------------------
换句话说,位于平面 t = 0 上 点的数据仅影响到锥点位于
点锥体边界上的解,这个解称为正向光锥(forward light cone),如图3所描绘。
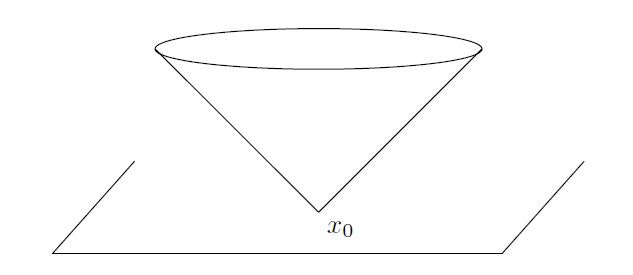
------------------------------------------------图 3 锥点位于(x,t )正向光锥--------------------------------------------
这样现象,称为Huygens原理,直接来自上面给出的 u 公式。
与这些考量相关的波动方程的另一个重要方面是有限传播速度(finite speed of propagation)。(在这种情况下,其中的 c = 1, 速度为1 。) 这意味着,如果我们的初始扰动位于 ,那么在有限的时间 t 之后,其影响将仅限于在以
为球心、半径为 | t | 为半径的球体内部传播。 为了准确地说明这一点,假设初始条件 f 和 g 在以
为球心、半径为 δ 的球中(认为δ很小)被支持。然后 u (x,t) 被支撑在以
为球心、半径为 | t | + δ 的球中。从上面的讨论中来看, 这个论断已经很清楚了。
3.3 R^2 ×ℝ ( )中的波动方程:降维求解法(The wave equation in
)中的波动方程:降维求解法(The wave equation in  :descent)
:descent)
一个明显的事实是,三维波动方程的解导出了二维波动方程的解。定义对应的均值为
。
定理 3.7 具有初始数据 的二维波动方程的Cauchy问题的一个解由
(8)
给出。注意与 d = 3 的这种情况之间的区别。此处,位于(x,t)的u取决于整个圆盘(半径长为 t 圆心位于 x )上的 f 和g ,并且不依赖于圆盘的边界附近的初始化。
在形式上,定理中的恒等式按如下方式出现。如果我们以 中的初始函数对f 和g 开始,我们可以考虑
对应的函数
和
,它们仅仅是函数 f 和g的扩展,其按
自变量是常量函数。即,
和
。
现在,假如 是具有初始数据
和
的三维波动方程的解(在前一节给出),则我们可以预期,则
也是按自变量
满足二维波动方程的常量。使用这个论据的一个难在于
和
不是寁降的,因为它们按自变量
是常量,因此,我们前面的方法不适用于这种情况。然而,很容易修改论据,以便获得对定理3.7的证明。
我们因定 T > 0 并考虑 ℝ 中的一个函数 ,使得只要
, 便有
。这个技巧是对按
作为自变量的函数
和
的截断,并考虑替换形式
和
。
现在 , 和
都属于
,因此,定理3.6提供了具有初始数据
和
的波动方程的一个解
。从这个公式容易看出,只要
且 |t |≤ T,
就是独立于
的。特别地,假如我们定义
,则当 |t |≤ T 时,u 满足二维波动方程。因为 T 是任意的,u 是我们问题的解之一,余下的问题就是理解为什么 u 是我们期望的形式。
根据球面坐标的定义,我们回想起函数 H 在球面 上的积分由
。
假如 H 不依赖于最后一个变量,即,对于某个两个变量的函数 h,有 ,则
。
为了计算最后一个积分,我们将积分按θ拆分成0到π/2和π/2到π两部分。通过变量替换 r = sin(θ),经过最后的极坐标变换,我们求得
。
将这个等式应用到 , h = f 和
, h = g , 我们求得公式 (8)给出的 u ,因此,定理3.7 的证明完成。
评述:
在一般 d 的情况下,波动方程的解共有我们在特殊情况 d = 1、2 和 3 中讨论过的许多属性。
在给定时间 t,x 点的初始数据仅影响特定区域内的解u。当 d > 1 为奇数时,数据仅影响锥点位于 x 的正向光锥边界上的点,而当 d = 1 或 d 为偶数时,数据影响正向光锥的所有点。 或者,点 (x, t ) 处的解仅取决于锥点位于 (x,t ) 处的反向光锥底部的数据。事实上,当 d > 1 为奇数时,只有基边界直接邻域的数据才会影响 u (x,t )。
波以有限速度传播:如果初始数据在有界集中得到支持,则解 u 的支持以速度 1 传播(如果波动方程未归一化,则更一般地为以速度 c 传播)。
我们可以通过以下对三维和二维波传播的不同行为的观察来说明其中一些事实。 由于光的传播受三维波动方程控制,因此,如果在 t = 0 时,光在原点发生闪光,则会发生以下情况:任何观察者都只能(在有限时间后)在一段时间内看到闪光。相反,考虑二维中发生的情况。如果我们把一块石头扔进湖里,湖面上的任何一点都将(在一段时间后)开始波动;尽管振荡的幅度会随着时间的推移而减小,但波动将(原则上)无限期地持续下去。
在一方面,当 d = 1 和 d = 3 时,以及在另一方面 d = 2 时,波动方程解的公式的特征不同,说明了 d 维Fourier分析中的一般原理:与偶数维的相应情况相比,在奇数维的情况下出现的大量公式更简单。我们将在下面看到几个进一步的例子。
4. 径向对称和Bessel函数(Radial symmetry and Bessel functions)
在前面我们观察到, 上的径向函数其Fourier变换还是径向函数。换句话说,对于某个
,假如
,则对于某个
,有
。一个自然的问题是,确定
与
之间的关系。
在一维和三维的情况下,这个问题有一个简单的答案。假如 d = 1,我们寻求的关系是
(9) 。
假如我们回顾 ℝ 仅有两个旋转的事实,即恒等旋转和按-1乘的旋转,则当函数是偶函数时,我们求得的函数恰好是径向函数。完成这个观察之后,很容易看出,假如 f 是径向的,且 |ξ| = ρ ,则
。
在 d = 3 的情况下, 和
之间的关系也相当简单,由公式
(10)
这个恒等式的证明基于引理 3.5 中给出的针对表面元素 dσ 的Fourier变换的公式:
。
更一般地说, 与
之间的关系可以用一族特殊函数来很好地表述,这些特殊函数在表现出径向对称性的问题中很自然地出现。
n∈ℤ 阶 Bessel 函数 ,用 表示,定义为函数
的第n项Fourier系数。因此,
,
于是,
。
作为这个定义的结果,当 d = 1时,我们求得 和
之间的关系是
(11) 。
事实上,因为 是径向的,我们取 ξ = (0, -ρ) 使得
,
正如预期。
通常,在 ,根据 (d /2) – 1 阶Bessel函数,存在相应的将
与
关联起来的公式(见问题2)。在偶数维的情况下,这些函数就是以上我们所定义的Bessel函数。对于奇数维的情况,我们需要一个更通用的Bessel函数定义来包含半积分阶。请注意,径向函数的Fourier变换公式给出了奇数维和偶数维之间差异的另一种说明。当 d = 1 或 d = 3(以及 d > 3、d 为奇数)时,公式采用初等函数形式,但当 d 为偶数时,情况并非如此。
5. Radon[ˈreɪ.dɑːn]变换及其一些应用(The Radon transform and some of its applications)
我们接下来讨论的积分变换由 Johann Radon(译注:1887-1956,奥地利数学家) 于 1917 年发明,在数学和其他科学领域有许多应用,其中包括在医学领域取得的重大成就。为了激发重建的定义和核心问题,我们首先提出Radon变换与医学成像理论中X射线扫描(或CAT扫描)的发展之间的密切联系。重建问题的解决,以及新算法和更快计算机的引入,都促进了计算机断层扫描(computerized tomography)的快速发展。在实践中,X 射线扫描提供了内部器官的“图片”,有助于检测和定位多种类型的异常。
在简要描述二维 X 射线扫描之后,我们定义了 X 射线变换并制定了反转该映射的基本问题。虽然这个问题在 中有显式解,但它比三维的类似问题更复杂,因此我们只在
中给出重构问题的完整解。这里我们有另一个例子,其中奇数维情况下的结果比偶数维情况下的结果更简单。
5.1 R^2 ( ) 上的X 射线变换(The X-ray transform in
) 上的X 射线变换(The X-ray transform in  )
)
考虑平铺于平面 上的一个二维对象 𝒪 ,我们可以将这个二维对象想象成一个人体器官的横截面的平面。
首先,我们假设 𝒪 是同质的(homogeneous),假如非常窄的 X 射线光子(photons)穿过这个物体。
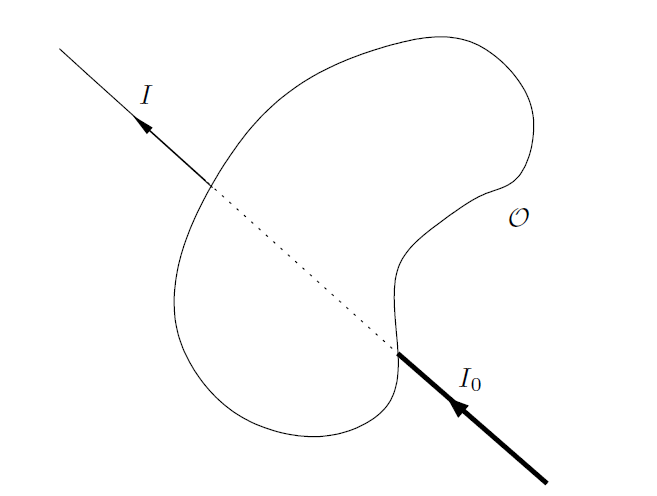
------------------------------------------------图 4 X 射线光束的衰减-----------------------------------------------
假如分别用 和
表示光束穿过 𝒪 之前和之后的强度,下面关系成立:
。
其中,d表示光束在物体中穿过的距离,ρ表示衰减系数(attenuation coefficient)或者吸收系数(absorption coefficient),其取决于𝒪的密度和其它物理特征。如果这个物体是非同质的,而是由两份种具有不同衰减系数 和
的材料组成,那么观察到的光束强度的递降由
给出,其中, 和
示光束在每种材料中穿过的距离。在任意物体的情况下,物体的密度和物理特征点到点地发生变化,这种衰减因子是
中的函数 ρ ,以上的关系成为
。
其中,L 表示 中光束的踪迹线,
表示 L 上ρ的线积分,由于我们所观察的
和 I所代表的意义,因此
实际上表示我们发射X 射线光束沿着线 L 穿过物体之后收集到的数据。由于我们在开始的时候可以按任意既定方向发射光束,所以,我们可以在
平面中对每一条线按以上积分。我们定义ρ 的X 射线的变换(或
中的Radon变换)为
。
注意,这个变换将 中每一个合适的函数 ρ (例如,
) 分配给
中其域是线集合 L 的另一个函数 X(ρ) 。
ρ 是未知量,且因为我们的最初兴趣点恰好在于物体的组合,现在的问题就成了从收集的数据重构函数ρ 。因此,我们提出了下面的重构问题:根据 X(ρ)求得 ρ 的一个公式。
在数学上,寻求该问题的公式就是要求给出 X 的逆的公式。这样的可逆公式实际上是否存在?作为第一步,我们提出下面的更简单的唯一性问题:假如 X(ρ) = X(ρ’ ),我们能够据此推断出 ρ = ρ’ 吗?
存在一个合理的先验期望(priori expectation),即 X(ρ)实际上决定了ρ ,正如我们可以通过统计所包含的维度(或自由度)所看到的那样。 上的函数 ρ 取决于2个参数(例如,
和
坐标)。类似地,线集合 L 的函数也取决于2个参数(例如,的斜率及其
截点)。在这种意义上,ρ 和 X(ρ)传达了相当数量的信息,因此,假设 X(ρ) 确定 ρ 是不合理的。
虽然对于 中的重建问题有一个令人满意的答案,并且对于唯一性问题也有一个肯定的答案,但我们在这里放弃它们。(但是,请参见练习 13 和问题 8。) 相反,我们将处理
中类似但更简单的情况。
最后,让我们指出,事实上,我们可以对 X射线变换进行采样,并仅确定有限多条线的 X(ρ)( L)。 因此,在实践中实施的重建方法不仅基于一般理论,而且还基于采样程序、数值近似和计算机算法。 事实证明,用于开发有效相关算法的方法是快速Fourier变换,我们将在下一章中顺便介绍它。
5.2 R^3 (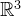 )上的Radon变换(The Radon transform in
)上的Radon变换(The Radon transform in  )
)
上一节中描述的实践也适用于三维情况。假如 𝒪 是 中取决于描述对象密度和物理特征的函数ρ的一个对象,对于
中的每一条线,发送一束 X 光束穿过物体 𝒪 取决于量
。
在 上,这个知识足以唯一地确定ρ ,但是,在
中,我们不需要这么多数据。事实上,通过使用上面计算自由度数量的启发式(heuristic)论据,我们看到对于
中的函数 ρ,该数量是 3,而确定
中的线 L 的参数数量是 4 (例如,对于
中的函数 ρ,该数量是 4)(例如,对于
平面中的截距,还有两个用于线方向的截距)。因此,从这个意义上说,问题是过度确定的(over-determined)。
我们转向二维问题的自然数学一般形式。在此,我们希望了解 所有平面(注:注意
上与点关联的维数,以及对于
平面相关的维数,在这两种情况下,维数都等于3 )的积分,从而确定
上的函数。为了表述准确,当我们提及一个平面的时候,我们指的是不必穿过原点的平面。如果 𝒫 是这样的一个平面,我们定义 Radon变换 ℛ( f ) 为
。
为了简化我们的表示,我们将遵循我们的实用假设,即,我们正在处理的函数是类
中的函数。然而,以下可获得的很多结果可以表明,Radon变换对于更广泛的函数类也是有效的。
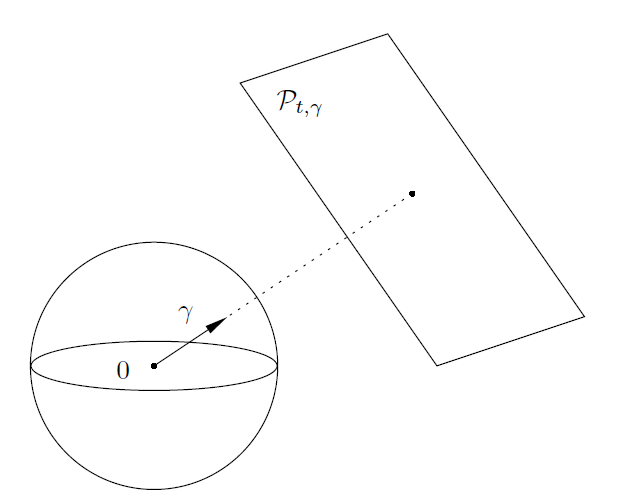
首先,我们解释f 在平面上的积分指的是什么。我们用作 中的平面的描述如下:已经一个单位向量
和一个数 t ∈ ℝ ,我们将平面
定义为
。
因此,我们用一个正交于平面的单位向量γ 以及平面到原点的距离 t 来参数化平面(如图5)。注意, ,以及我们允许 t 取负值。
----------------------------------------------图 5 中的平面的描述------------------------------------------
已经一个函数 ,我们必须赋予其在平面
上的积分的意义。我们按随后的方式进行。选择单位向量
使得
和γ 对
是正交基。则,任意
可以写成
,其中,
且
。
假如 ,我们定义
(12) 。
为了一致性,我们必须确保定义与向量 的选择无关。
命题 5.1 假如 ,则对于每一个 γ,
的定义独立于
的选择。此外,
。
证明:
如果 ,
是另一个选择的基向量,因此,γ ,
,
是正交的,考虑
上的旋转 R ,其将
带到
,将
带到
。在积分式中作变量替换
,证明了我们的定义(12)是独立于基的选择的。
为了证明这个公式,令 R 表示在 中取标准单位向量基(在些,我们指的是单位向量(1,0,0), (0,1,0), (0,0,1))到 γ,
,
的旋转。则
。
评述:我们离题指出,X 射线变换决定了 Radon 变换,因为二维积分可以表示为迭代的一维积分。 换句话说,函数在所有线上的积分的知识决定了该函数在任何平面上的积分。
处理完这些预置事项之后,我们转向研究原来的问题。 的函数的Radon 变换定义为
。
特别是,我们看到,Radon 变换是 上平面集上的函数。从给予的平面参数化表述,我们可以等价地将 ℛ( f ) 视为乘积
上的函数,其中,
表示
的单位球面。
上的函数类由那些按 t,γ 一致地满足 Schwartz条件的函数构成。换句话说,我们定义
为所有可以按 t 无限可微的连续函数 F( t,γ ),且满足
(对于所有 k, 𝓁 > 0) 。
我们的目标是为了解决下面的问题。
唯一性问题:假如 ℛ( f ) = ℛ( g ) ,则 f = g 。
重构问题:根据 ℛ( f )来表述 f 。
将通过使用Fourier变换来求解。事实上,关键点在于Radon变换和Fourier变换之间的这种非常优雅而本质的关系。
引理 5.2 假如 ,则对于每一个固定的γ,有 ℛ( f )( t,γ) ∈ 𝒮(ℝ) 。此外,
。
确切地说, 表示 f 的(三维) Fourier变换, 而
表示
固定γ并作为 t 的函数的一维Fourier 变换。
证明:
因为 ,对于任意一个正整数 N,存在一个常量
使得
,
假如我们回顾事实 x = tγ + u ,其中,γ 正交于 u 。只此,只要 N ≥ 3,我们就能求得
。
对导数的论证可证明对于每一个固定的γ , ℛ( f )( t,γ)∈ 𝒮(ℝ) 。
为了建立恒等式,我们首先注意到
。
然而,因为 γ.u = 0 ,以及 |γ| = 1,我们可以写成
。
因此,我们求得
。
最后,在 中,一个从向量 γ,
,
到标准基的旋转证明了
,正如预期。
作为恒等式的结论,我们可以肯定地回答在 中 的 Radon变换的唯一性问题。
推论 5.3 假如 且 ℛ( f ) = ℛ( g ) , 则 f = g 。
应用引理到差 f - g 并使用逆 Fourier变换定理,可以推导出推论的证明。
我们最后的任务是给出将原函数f从其Radon变换中恢复回来的公式。因为 ℛ( f )为空间 平面集上的函数,f 是空间变量
的函数,为了恢复 f 我们引入双重(dual) Radon变换,它将定义在平面上的函数传递到定义于
中的函数。
已知 上的一个函数 F,我们定义其双重Radon变换为
(13) 。
观察到,当且仅当 x.γ = t 时,某一点 x 才属于 ,因此,这里的思想是,已知
,我们通过对 F 在穿过 x 的所有平面的子集上进行积分,从而求得
,即,
,
其中右侧积分的确切含义在(13)中给出。由于我们有随合的观察事实,所以我们使用了术语“双重(dual)”。假如 具有Hermit内积
,
并且 具有Hermit内积
,
则, ,
,
且
(14) 。
这个恒等式的有效性不必在下面论证,对其验证留给读者作习题。
现在我们表述重构定理。
定理5.4 假如 , 则
。
我们记得, Laplace 算子是 。
证明:
根据我们前面的引理,我们有
。
因此,
,
从而,
。
在第一行,我们在积分符号下进行微分(译注:两次微分),并利于事实 (因为 |γ| = 1)。最后一步从
中的极坐标公式和逆Fourier变换定理推导出来。
5.3 关于平面波的一点说明(A note about plane waves)
我们通过简要地提及Radon变换和波动方程解之间的良好联系来结束本章。 这是通过以下方式实现的。 回想一下,当 d = 1 时,波动方程的解可以表示为行波之和(参见第 1 章),并且很自然地会问,在更高维中是否存在此类行波的类似情况。答案如下。令 F 为单变量函数,我们假设其足够平滑(比如, ),并考察函数 u (x, t),定义为
。
其中, ,γ 是
中的单位向量。很容易直接验证 u 是
(具有 c = 1)中波动方程的一个解。这样的一个解称为平面波(plane wave);事实上,注意到,在每一个垂直于γ 方向的平面上,u 都是一个常量,且随着时间的演进,波会沿着γ 方向传输。(应当说明,当 d > 1 时,平面波不是
上的函数,原因在于在垂直于γ 的方向上它们是常量(注:顺便说一句,这一观察结果进一步表明,对波动方程进行更全面的处理需要取消函数属于
的限制)。)
基本事实是,当 d > 1 时,波动方程的解可以写成平面波的积分(与 d = 1 时的和相反);这实际上可以通过初始数据 f 和 g 的 Radon 变换来完成。d = 3时的相关公式见问题6。
内容来源:
<<Fourier Analysis: An Introduction>> E.M. Stein & R. Shakarchi