[论文精读]How Powerful are Graph Neural Networks?

论文原文：[1810.00826] How Powerful are Graph Neural Networks? (arxiv.org)

英文是纯手打的！论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误，若有发现欢迎评论指正！文章偏向于笔记，谨慎食用！

1. 省流版

1.1. 心得

①Emm, 数学上的解释性确实很强了

②他一直在...在说引理

1.2. 论文框架图

2. 论文逐段精读

2.1. Abstract

①Even though the occurrence of Graph Neural Networks (GNNs) changes graph representation learning to a large extent, it and its variants are all limited in representation abilities.

2.2. Introduction

①Briefly introduce how GNN works (combining node information from k-hop neighbors and then pooling)

②The authors hold the view that ⭐ other graph models mostly based on plenty experimental trial-and-errors rather than theoretical understanding

③They combine GNNs and the Weisfeiler-Lehman (WL) graph isomorphism test to build a new framework, which relys on multisets

④GIN is excellent in distinguish, capturing and representaion

heuristics n.[U] (formal) 探索法；启发式

heuristic adj.(教学或教育)启发式的

2.3. Preliminaries

（1）Their definition

①They define two tasks: node classicifation with node label $y_{v}$ and graph classification with graph label $y_{i},i\in \left \{ 1,2...,N \right \}$

（2）Other models

①The authors display the function of GNN in the $k$ -th layer:

$a_v^{(k)}=\text{AGGREGATE}^{(k)}\left(\left\{h_u^{(k-1)}:u\in\mathcal{N}(v)\right\}\right),\\\quad h_v^{(k)}=\text{COMBINE}^{(k)}\left(h_v^{(k-1)},a_v^{(k)}\right),$

where only $h_{v}^{(0)}$ is initialized to $X_{v}$ （其余细节就不多说了，在GNN的笔记里都有）

②Pooling layer of GraphSAGE, the AGGREGATE function is:

$a_v^{(k)}=\text{MAX}\left(\left\{\text{ReLU}\left(W\cdot h_u^{(k-1)}\right),\forall u\in\mathcal{N}(v)\right\}\right)$

where MAX is element-wise max-pooling operator;

$W$ is learnable weight matrix;

and followed by concatenated COMBINE and linear mapping $W\cdot\left[h_{v}^{(k-1)},a_{v}^{(k)}\right]$

③AGGREGATE and COMBINE areintegrated in GCN:

$h_v^{(k)}=\text{ReLU}\left(W\cdot\text{MEAN}\left\{h_u^{(k-1)},\forall u\in\mathcal{N}(v)\cup\{v\}\right\}\right)$

④Lastly follows a READOUT layer to get final prediction answer:

$h_G=\text{READOUT}\big(\big\{h_v^{(K)}\big|v\in G\big\}\big)$

where the READOUT function can be different forms

（3）Weisfeiler-Lehman (WL) test

①WL firstly aggregates nodes and their neighborhoods and then hashs the labels (??hash?这好吗)

②Based on WL, WL subtree kernel was proposed to evaluate the similarity between graphs

③A subtree of height $k$ 's root node is the node at $k$ -th iteration

permutation n.置换;排列(方式);组合(方式)

2.4. Theoretical framework: overview

①The framework overview

②Multiset: is a 2-tuple $X=(S,m)$ , where "where $S$ is the underlying set of $X$ that is formed from its distinct elements, and $m:S\rightarrow \mathbb{N}_{\geq 1}$ gives the multiplicity of the elements" （我没有太懂这句话欸）

③They are not allowed that GNN map different neighbors to the same representation. Thus, the aggregation must be injective （我也不造为啥）

2.5. Building powerful graph neural networks

①They define Lemma 2, namely WL graph isomorphism test is able to correctly distinguish non-isomorphic graphs

②Theorem 3 完全没看懂

③Lemma 4: If input feature space is countable, then the space of node hidden features $h_{v}^{(k)}$ is also countable

2.5.1. Graph isomorphism network (GIN)

①Lemma 5: there is $f:\mathcal{X}\rightarrow\mathbb{R}^{n}$ , which makes $h(X)=\sum_{x\in X}f(x)$ unique in $X\subset \mathcal{X}$ . Also there is $g\left(X\right)=\phi\left(\sum_{x\in X}f(x)\right)$

②Corollary 6: there is unique $\begin{aligned}h(c,X)=(1+\epsilon)\cdot f(c)+\sum_{x\in X}f(x)\end{aligned}$ and $g\left(c,X\right)=\varphi\left(\left(1+\epsilon\right)\cdot f(c)+\sum_{x\in X}f(x)\right)$ .

③Finally, the update function of GIN can be:

$h_{v}^{(k)}=\mathrm{MLP}^{(k)}\left(\left(1+\epsilon^{(k)}\right)\cdot h_{v}^{(k-1)}+\sum_{u\in\mathcal{N}(v)}h_{u}^{(k-1)}\right)$

2.5.2. Graph-level readout of GIN

①Sum, mean and max aggregators:

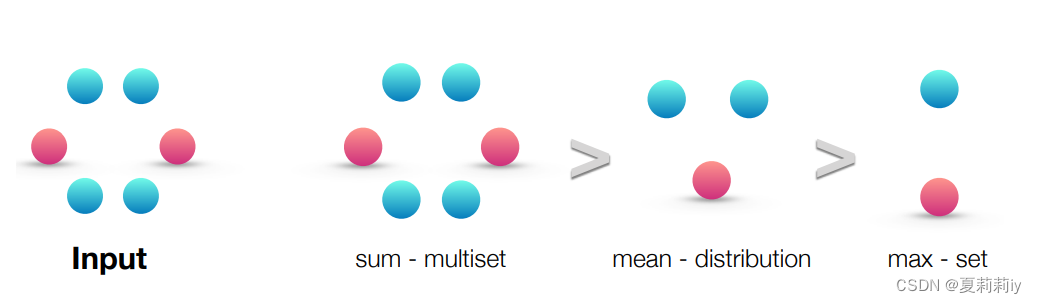
②The fail examples when the different $v$ and ${v}'$ map the same embedding:

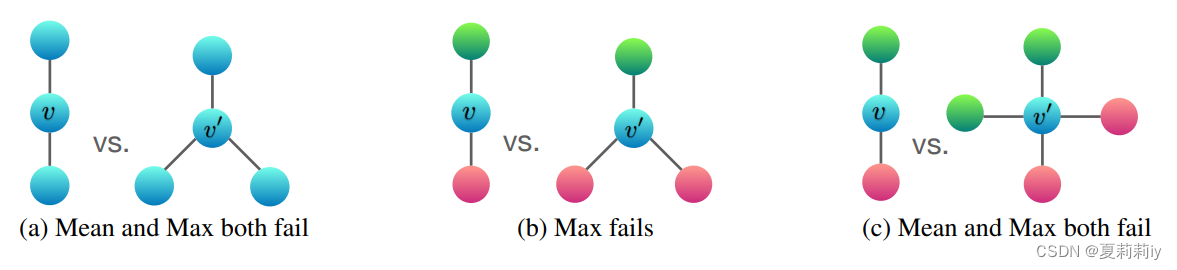
where (a) represents all the nodes are the same, only sum can distinguish them;

blue in (b) represents the max, thus max fails to distinguish as well;

same in (c). （盲猜这里其实蓝色v自己是一个节点，但是没有考虑自己的特征，而是纯看1-hop neighborhoods）

③They change the READOUT layer to:

$h_G=\text{CONCAT}\Big(\text{READOUT}\Big(\Big\{h_v^{(k)}|v\in G\Big\}\Big)\big|k=0,1,\ldots,K\Big)$

2.6. Less powerful but still interesting GNNs

They designed ablation studies

2.6.1. 1-layer perceptrons are not sufficient

①1-layer perceptrons are akin to linear mapping, which is far insufficient for distinguishing

②Lemma 7: notwithstanding multiset $X_{1}$ is different from $X_{2}$ , they might get the same results: $\sum_{x\in X_1}\text{ReLU}\left(Wx\right)=\sum_{x\in X_2}\text{ReLU}\left(Wx\right)$

2.6.2. Structures that confuse mean and max-pooling

这一节的内容在2.5.2.②的图下已经解释过了

2.6.3. Mean learns distributions

①Collary 8: there is a function $h\left ( X \right )=\frac{1}{\left | X \right |}\sum_{x\in X}f\left ( x \right )$ . If and only if multisets $X_{1}$ and $X_{2}$ are the same distribution, $h\left ( X_{1} \right )=h\left ( X_{2} \right )$

②When statistical and distributional information in graph cover more important part, mean aggregator performs better. But when structure is valued more, mean aggregator may do worse.

③Sum and mean aggregator may be similar when node features are multifarious and hardly repeat

2.6.4. Max-pooling learns sets with distinct elements

①Max aggregator focus on learning the structure of graph (原文用的"skeleton"而不是"structure"), and it has a certain ability to resist noise and outliers

②For max function $h\left ( X \right )=max_{x\in X}f\left ( x \right )$ , if and only if $X_{1}$ and $X_{2}$ have the same underlying set, $h\left ( X_{1} \right )=h\left ( X_{2} \right )$

2.6.5. Remarks on other aggregators

①They do not cover the analysis of weighted average via attention or LSTM pooling

2.7. Other related work

①Traditional GNN does not provide enough math explanation

②Exceptionally, RKHS of graph kernels (?) is able to approximate measurable functions in probability

③Also, they can hardly generalize to multple architectures

2.8. Experiments

①Dataset: 9 graph classification benchmarks: 4 bioinformatics datasets (MUTAG, PTC, NCI1, PROTEINS) and 5 social network datasets (COLLAB, IMDB-BINARY, IMDB-MULTI, REDDITBINARY and REDDIT-MULTI5K)

②Social networks are lack of node features, then they set node vectors as the same in REDDIT and use one hot encoding for others

2.8.1. Results

2.9. Conclusion

3. 知识补充